Workshop 9.7a - Nested designs (mixed effects models)
4 August 2011
Basic statistics references
- Logan (2010) - Chpt 12-14
- Quinn & Keough (2002) - Chpt 9-11
Very basic overview of Randomized block
Nested ANOVA - one between factor
In an unusually detailed preparation for an Environmental Effects Statement for a proposed discharge of dairy wastes into the Curdies River, in western Victoria, a team of stream ecologists wanted to describe the basic patterns of variation in a stream invertebrate thought to be sensitive to nutrient enrichment. As an indicator species, they focused on a small flatworm, Dugesia, and started by sampling populations of this worm at a range of scales. They sampled in two seasons, representing different flow regimes of the river - Winter and Summer. Within each season, they sampled three randomly chosen (well, haphazardly, because sites are nearly always chosen to be close to road access) sites. A total of six sites in all were visited, 3 in each season. At each site, they sampled six stones, and counted the number of flatworms on each stone.
Download Curdies data set
| Format of curdies.csv data files | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||||||||||||||||||||||||||||
The hierarchical nature of this design can be appreciated when we examine an illustration of the spatial and temporal scale of the measurements.

- Within each of the two Seasons, there were three separate Sites (Sites not repeatidly measured across Seasons).
- Within each of the Sites, six logs were selected (haphazardly) from which the number of flatworms were counted.
curdies <- read.table("../downloads/data/curdies.csv", header = T, sep = ",", strip.white = T) head(curdies)
## SEASON SITE DUGESIA S4DUGES ## 1 WINTER 1 0.6477 0.8971 ## 2 WINTER 1 6.0962 1.5713 ## 3 WINTER 1 1.3106 1.0700 ## 4 WINTER 1 1.7253 1.1461 ## 5 WINTER 1 1.4594 1.0991 ## 6 WINTER 1 1.0576 1.0141
curdies$SITE <- as.factor(curdies$SITE)
Notice the data set - each of the nested factors is labelled differently - there can be no replicate for the random (nesting) factor.
- H0 Effect 1:
- H0 Effect 2:
| Assumption | Diagnostic/Risk Minimization |
|---|---|
| I. | |
| II. | |
| III. |
library(nlme) curdies.ag <- gsummary(curdies, form = ~SEASON/SITE, base:::mean) # OR library(plyr) curdies.ag <- ddply(curdies, ~SEASON + SITE, numcolwise(mean))
boxplot(DUGESIA ~ SEASON, curdies.ag)
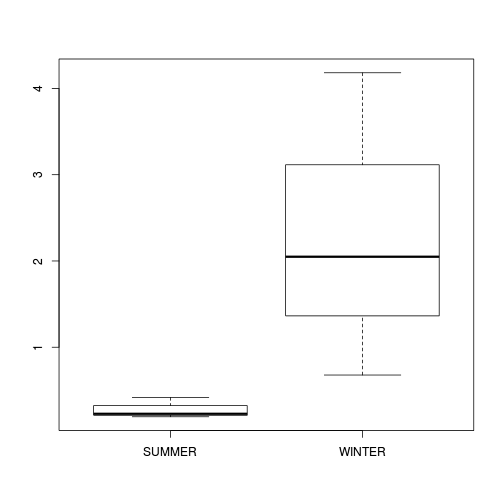
If so, assess whether a transformation will address the violations (HINT) and then make the appropriate corrections
curdies$S4DUGES <- sqrt(sqrt(curdies$DUGESIA)) curdies.ag <- gsummary(curdies, form = ~SEASON/SITE, base:::mean) boxplot(S4DUGES ~ SEASON, curdies.ag)
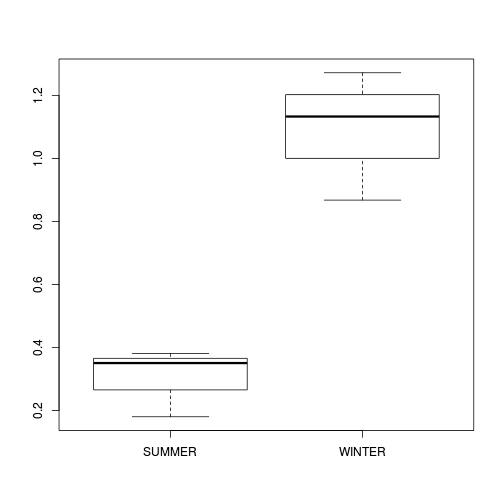
| Effect | Nominator (Mean Sq, df) | Denominator (Mean Sq, df) |
|---|---|---|
| SEASON | ||
| SITE |
S4DUGES = SEASON + SITE + CONSTANT
using a nested ANOVA (HINT). Fill (HINT) out the table below, make sure that you have treated SITE as a random factor when compiling the overall results.
curdies.aov <- aov(S4DUGES ~ SEASON + Error(SITE), data = curdies) summary(curdies.aov)
## ## Error: SITE ## Df Sum Sq Mean Sq F value Pr(>F) ## SEASON 1 5.57 5.57 34.5 0.0042 ** ## Residuals 4 0.65 0.16 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Error: Within ## Df Sum Sq Mean Sq F value Pr(>F) ## Residuals 30 4.56 0.152
summary(lm(curdies.aov))
## ## Call: ## lm(formula = curdies.aov) ## ## Residuals: ## Min 1Q Median 3Q Max ## -0.381 -0.262 -0.138 0.165 0.902 ## ## Coefficients: (1 not defined because of singularities) ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.3811 0.1591 2.40 0.0230 * ## SEASONWINTER 0.7518 0.2250 3.34 0.0022 ** ## SITE2 0.1389 0.2250 0.62 0.5416 ## SITE3 -0.2651 0.2250 -1.18 0.2480 ## SITE4 -0.0303 0.2250 -0.13 0.8938 ## SITE5 -0.2007 0.2250 -0.89 0.3795 ## SITE6 NA NA NA NA ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.39 on 30 degrees of freedom ## Multiple R-squared: 0.577, Adjusted R-squared: 0.507 ## F-statistic: 8.19 on 5 and 30 DF, p-value: 5.72e-05
library(gmodels) ci(lm(curdies.aov))
## Estimate CI lower CI upper Std. Error p-value ## (Intercept) 0.3811 0.05622 0.7060 0.1591 0.023031 ## SEASONWINTER 0.7518 0.29235 1.2113 0.2250 0.002242 ## SITE2 0.1389 -0.32055 0.5984 0.2250 0.541560 ## SITE3 -0.2651 -0.72455 0.1944 0.2250 0.247983 ## SITE4 -0.0303 -0.48978 0.4292 0.2250 0.893763 ## SITE5 -0.2007 -0.66013 0.2588 0.2250 0.379548
| Source of variation | df | Mean Sq | F-ratio | P-value |
|---|---|---|---|---|
| SEASON | ||||
| SITE | ||||
| Residuals |
| Estimate | Mean | Lower 95% CI | Upper 95% CI |
|---|---|---|---|
| Summer | |||
| Effect size (Winter-Summer) |
Normally, we are not interested in formally testing the effect of the nested factor to get the correct F test for the nested factor (SITE), examine a representation of the anova table of the fitted linear model that assumes all factors are fixed (HINT)
library(nlme) curdies.lme <- lme(S4DUGES ~ SEASON, random = ~1 | SITE, data = curdies) summary(curdies.lme)
## Linear mixed-effects model fit by REML ## Data: curdies ## AIC BIC logLik ## 46.43 52.54 -19.21 ## ## Random effects: ## Formula: ~1 | SITE ## (Intercept) Residual ## StdDev: 0.04009 0.3897 ## ## Fixed effects: S4DUGES ~ SEASON ## Value Std.Error DF t-value p-value ## (Intercept) 0.3041 0.09472 30 3.211 0.0031 ## SEASONWINTER 0.7868 0.13395 4 5.873 0.0042 ## Correlation: ## (Intr) ## SEASONWINTER -0.707 ## ## Standardized Within-Group Residuals: ## Min Q1 Med Q3 Max ## -1.2065 -0.7681 -0.2481 0.3531 2.3209 ## ## Number of Observations: 36 ## Number of Groups: 6
# Calculate the confidence interval for the effect size of the main effect of season intervals(curdies.lme)
## Approximate 95% confidence intervals ## ## Fixed effects: ## lower est. upper ## (Intercept) 0.1107 0.3041 0.4976 ## SEASONWINTER 0.4148 0.7868 1.1587 ## attr(,"label") ## [1] "Fixed effects:" ## ## Random Effects: ## Level: SITE ## lower est. upper ## sd((Intercept)) 1.88e-07 0.04009 8546 ## ## Within-group standard error: ## lower est. upper ## 0.3026 0.3897 0.5019
# unique(confint(curdies.lme,'SEASONWINTER')[[1]]) Examine the ANOVA table with Type I (sequential) # SS anova(curdies.lme)
## numDF denDF F-value p-value ## (Intercept) 1 30 108.5 <.0001 ## SEASON 1 4 34.5 0.0042
library(lme4)
curdies.lmer <- lmer(S4DUGES ~ SEASON + (1 | SITE), data = curdies) summary(curdies.lmer)
## Linear mixed model fit by REML ## Formula: S4DUGES ~ SEASON + (1 | SITE) ## Data: curdies ## AIC BIC logLik deviance REMLdev ## 46.4 52.8 -19.2 32.5 38.4 ## Random effects: ## Groups Name Variance Std.Dev. ## SITE (Intercept) 1.16e-13 3.41e-07 ## Residual 1.53e-01 3.91e-01 ## Number of obs: 36, groups: SITE, 6 ## ## Fixed effects: ## Estimate Std. Error t value ## (Intercept) 0.3041 0.0922 3.30 ## SEASONWINTER 0.7868 0.1304 6.03 ## ## Correlation of Fixed Effects: ## (Intr) ## SEASONWINTE -0.707
# Calculate the confidence interval for the effect size of the main effect of season # library(gmodels) ci(curdies.lmer) library(languageR)
## Error: package 'languageR' was built before R 3.0.0: please re-install it
pvals.fnc(curdies.lmer, withMCMC = FALSE, addPlot = F)
## Error: could not find function "pvals.fnc"
# Examine the effect season via a likelihood ratio test curdies.lmer1 <- lmer(S4DUGES ~ SEASON + (1 | SITE), data = curdies, REML = F) curdies.lmer2 <- lmer(S4DUGES ~ 1 + (1 | SITE), data = curdies, REML = F) anova(curdies.lmer1, curdies.lmer2, test = "F")
## Data: curdies ## Models: ## curdies.lmer2: S4DUGES ~ 1 + (1 | SITE) ## curdies.lmer1: S4DUGES ~ SEASON + (1 | SITE) ## Df AIC BIC logLik Chisq Chi Df Pr(>Chisq) ## curdies.lmer2 3 51.8 56.6 -22.9 ## curdies.lmer1 4 40.5 46.9 -16.3 13.3 1 0.00026 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
library(ez)
## Error: package 'ez' was built before R 3.0.0: please re-install it
ezStats(dv = .(S4DUGES), between = .(SEASON), wid = .(SITE), data = curdies)
## Error: could not find function "ezStats"
library(ez)
## Error: package 'ez' was built before R 3.0.0: please re-install it
ezANOVA(dv = .(S4DUGES), between = .(SEASON), wid = .(SITE), data = curdies, type = 3)
## Error: could not find function "ezANOVA"
library(gplots)
library(AICcmodavg) curdies.predict <- predictSE.mer(curdies.lmer, newdata = data.frame(SEASON = c("SUMMER", "WINTER")))
## Error: no applicable method for 'fixef' applied to an object of class "mer"
par(mar = c(5, 5, 1, 1)) plot(1:2, curdies.predict$fit, type = "n", axes = F, ann = F, ylim = range(0, 1.5), xlim = c(0.5, 2.5))
## Error: object 'curdies.predict' not found
plotCI(curdies.predict$fit, uiw = curdies.predict$se.fit * 2, las = 1, add = T, sfrac = 0.001)
## Error: object 'curdies.predict' not found
axis(1, at = c(1, 2), lab = levels(curdies$SEASON))
## Error: plot.new has not been called yet
axis(2, las = 1)
## Error: plot.new has not been called yet
mtext("Number of Dugesia per stone", 2, line = 3, cex = 1.25)
## Error: plot.new has not been called yet
mtext("Season", 1, line = 3, cex = 1.25)
## Error: plot.new has not been called yet
box(bty = "l")
## Error: plot.new has not been called yet
# OR the more flexible way, but that requires more code and thought: newdata <- expand.grid(SEASON = c("SUMMER", "WINTER"), S4DUGES = 0) mod.mat <- model.matrix(terms(curdies.lmer), newdata) newdata$S4DUGES = mod.mat %*% fixef(curdies.lmer)
## Error: no applicable method for 'fixef' applied to an object of class "mer"
pvar1 <- (diag(mod.mat %*% tcrossprod(vcov(curdies.lmer), mod.mat)))
## Error: no applicable method for 'vcov' applied to an object of class "mer"
tvar1 <- pvar1 + VarCorr(curdies.lmer)$SITE[1]
## Error: object 'pvar1' not found
newdata <- data.frame(newdata, plo = newdata$S4DUGES - 2 * sqrt(pvar1), phi = newdata$S4DUGES + 2 * sqrt(pvar1), tlo = newdata$S4DUGES - 2 * sqrt(tvar1), thi = newdata$S4DUGES + 2 * sqrt(tvar1))
## Error: object 'pvar1' not found
par(mar = c(5, 5, 1, 1)) plot(S4DUGES ~ as.numeric(SEASON), newdata, type = "n", axes = F, ann = F, ylim = range(0, newdata$phi), xlim = c(0.5, 2.5)) points(curdies$DUGESIA ~ jitter(as.numeric(curdies$SEASON)), pch = 16, col = "grey") with(newdata, arrows(as.numeric(SEASON), plo, as.numeric(SEASON), phi, ang = 90, length = 0.05, code = 3))
## Error: object 'plo' not found
with(newdata, points(as.numeric(SEASON), S4DUGES, pch = 21, bg = "black", col = "black")) axis(1, at = c(1, 2), lab = newdata$SEASON) axis(2, las = 1) mtext("Number of Dugesia per stone", 2, line = 3, cex = 1.25) mtext("Season", 1, line = 3, cex = 1.25) box(bty = "l")
# newdataTransformed <- expand.grid(SEASON=c('SUMMER','WINTER')) library(AICcmodavg) # newdataTransformed <- # data.frame(newdataTransformed,predictSE.mer(curdies.lmer,newdataTransformed, print.matrix=T)^4) newdata[, -1] <- newdata[, -1]^4 par(mar = c(5, 5, 1, 1)) plot(S4DUGES ~ as.numeric(SEASON), newdata, type = "n", axes = F, ann = F, ylim = range(newdata$plo, newdata$phi), xlim = c(0.5, 2.5))
## Warning: no non-missing arguments to min; returning Inf
## Warning: no non-missing arguments to max; returning -Inf
## Error: need finite 'ylim' values

points(curdies$DUGESIA ~ jitter(as.numeric(curdies$SEASON)), pch = 16, col = "grey") with(newdata, arrows(as.numeric(SEASON), plo, as.numeric(SEASON), phi, ang = 90, length = 0.05, code = 3))
## Error: object 'plo' not found
with(newdata, points(as.numeric(SEASON), S4DUGES, pch = 21, bg = "black", col = "black")) # plot(fit~as.numeric(SEASON), newdata, type='n', axes=F, ann=F, ylim=range(0,2),xlim=c(0.5,2.5)) # with(newdata,arrows(as.numeric(SEASON),fit-2*se.fit,as.numeric(SEASON),fit+2*se.fit, ang=90, # length=0.05, code=3)) with(newdata, points(as.numeric(SEASON),fit, pch=21, # bg='black',col='black')) axis(1, at = c(1, 2), lab = newdata$SEASON) axis(2, las = 1) mtext("Number of Dugesia per stone", 2, line = 3, cex = 1.25) mtext("Season", 1, line = 3, cex = 1.25) box(bty = "l")
library(gplots) library(AICcmodavg) curdies.predict <- predictSE.mer(curdies.lmer, newdata = data.frame(SEASON = c("SUMMER", "WINTER")))
## Error: no applicable method for 'fixef' applied to an object of class "mer"
curdies.predict$fit <- curdies.predict$fit^2
## Error: object 'curdies.predict' not found
curdies.predict$se.fit <- curdies.predict$se.fit^2
## Error: object 'curdies.predict' not found
par(mar = c(5, 5, 1, 1)) plot(1:2, curdies.predict$fit, type = "n", axes = F, ann = F, ylim = range(0, 1.5), xlim = c(0.5, 2.5))
## Error: object 'curdies.predict' not found
plotCI(curdies.predict$fit, uiw = curdies.predict$se.fit * 2, las = 1, add = T, sfrac = 5e-04)
## Error: object 'curdies.predict' not found
axis(1, at = c(1, 2), lab = levels(curdies$SEASON))
## Error: plot.new has not been called yet
axis(2, las = 1)
## Error: plot.new has not been called yet
mtext("Number of Dugesia per stone", 2, line = 3, cex = 1.25)
## Error: plot.new has not been called yet
mtext("Season", 1, line = 3, cex = 1.25)
## Error: plot.new has not been called yet
box(bty = "l")
## Error: plot.new has not been called yet
library(nlme) nlme:::VarCorr(lme(S4DUGES ~ 1, random = ~1 | SEASON/SITE, curdies))
## Variance StdDev ## SEASON = pdLogChol(1) ## (Intercept) 0.300523 0.54820 ## SITE = pdLogChol(1) ## (Intercept) 0.001607 0.04009 ## Residual 0.151851 0.38968
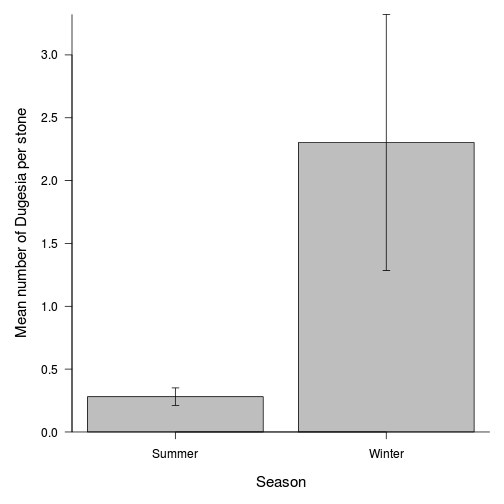
- What influences the abundance of Dugesia
- Where best to focus sampling effort to maximize statistical power?
opar <- par(mar = c(5, 5, 1, 1)) means <- tapply(curdies.ag$DUGESIA, curdies.ag$SEASON, mean) sds <- tapply(curdies.ag$DUGESIA, curdies.ag$SEASON, sd) lens <- tapply(curdies.ag$DUGESIA, curdies.ag$SEASON, length) ses <- sds/sqrt(lens) xs <- barplot(means, beside = T, ann = F, axes = F, ylim = c(0, max(means + ses)), axisnames = F) arrows(xs, means - ses, xs, means + ses, code = 3, length = 0.05, ang = 90) axis(1, at = xs, lab = c("Summer", "Winter")) mtext("Season", 1, line = 3, cex = 1.25) axis(2, las = 1) mtext("Mean number of Dugesia per stone", 2, line = 3, cex = 1.25) box(bty = "l")