Jump to main navigation

«
»

Workshop 9.6a - Factorial Analysis of Variance

5 July 2011

Factorial ANOVA references

  • Logan (2010) - Chpt 12
  • Quinn & Keough (2002) - Chpt 9
Very basic overview of Nested ANOVA

Very basic overview of Two-Factor ANOVA

Exercise 2 - Two factor ANOVA

A biologist studying starlings wanted to know whether the mean mass of starlings differed according to different roosting situations. She was also interested in whether the mean mass of starlings altered over winter (Northern hemisphere) and whether the patterns amongst roosting situations were consistent throughout winter, therefore starlings were captured at the start (November) and end of winter (January). Ten starlings were captured from each roosting situation in each season, so in total, 80 birds were captured and weighed.

Download Starling data set

Format of starling.csv data files
SITUATIONMONTHMASSGROUP
S1November78S1Nov
........
S2November78S2Nov
........
S3November79S3Nov
........
S4November77S4Nov
........
S1January85S1Jan
........
SITUATIONCategorical listing of roosting situations
MONTHCategorical listing of the month of sampling.
MASSMass (g) of starlings.
GROUPCategorical listing of situation/month combinations - used for checking ANOVA assumptions
Starlings

Open the starling data file.

Show code
starling <- read.table("../downloads/data/starling.csv", header = T, sep = ",", strip.white = T)
head(starling)

##   SITUATION    MONTH MASS GROUP
## 1        S1 November   78 S1Nov
## 2        S1 November   88 S1Nov
## 3        S1 November   87 S1Nov
## 4        S1 November   88 S1Nov
## 5        S1 November   83 S1Nov
## 6        S1 November   82 S1Nov

Q2-1. List the 3 null hypothesis being tested

Q2-2. Test the assumptions
by producing boxplots
(HINT) and mean vs variance plot
.
Show code
boxplot(MASS ~ SITUATION * MONTH, data = starling)
plot of chunk Q2-2
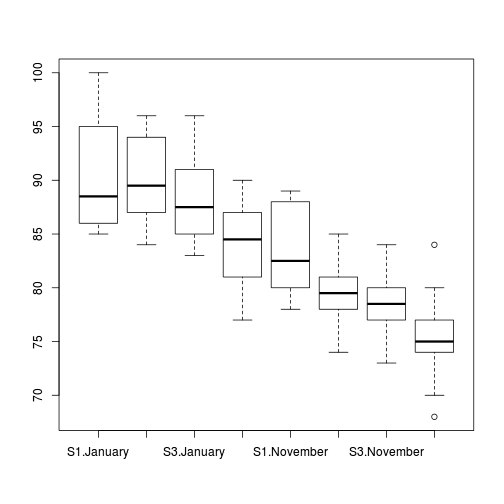
means <- with(starling, tapply(MASS, list(SITUATION, MONTH), mean))
vars <- with(starling, tapply(MASS, list(SITUATION, MONTH), var))
plot(means, vars, pch = 16)
plot of chunk Q2-2
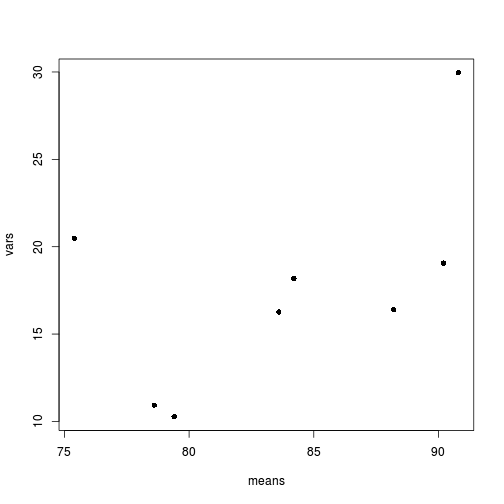
  1. Is there any evidence that one or more of the assumptions are likely to be violated? (Y or N)
  2. Is the proposed model balanced?
    (Y or N)
    3. Show code
    replications(MASS ~ SITUATION * MONTH, data = starling)

    ##       SITUATION           MONTH SITUATION:MONTH 
##              20              40              10

    !is.list(replications(MASS ~ SITUATION * MONTH, data = starling))

    ## [1] TRUE

Q2-3. Now fit a two-factor ANOVA model (HINT)
and examine the residuals (HINT).

Show code
starling.lm <- lm(MASS ~ SITUATION * MONTH, data = starling)
# setup a 2x6 plotting device with small margins
par(mfrow = c(2, 1), oma = c(0, 0, 2, 0))
plot(starling.lm, ask = F, which = 1:2)
plot of chunk Q1-2a
Any evidence of skewness or unequal variances? Any outliers? Any evidence of violations? ('Y' or 'N') .
Examine the ANOVA table
Show code
summary(starling.lm)

## 
## Call:
## lm(formula = MASS ~ SITUATION * MONTH, data = starling)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##   -7.4   -3.2   -0.4    2.9    9.2 
## 
## Coefficients:
##                           Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                  90.80       1.33   68.26  < 2e-16 ***
## SITUATIONS2                  -0.60       1.88   -0.32  0.75069    
## SITUATIONS3                  -2.60       1.88   -1.38  0.17121    
## SITUATIONS4                  -6.60       1.88   -3.51  0.00078 ***
## MONTHNovember                -7.20       1.88   -3.83  0.00027 ***
## SITUATIONS2:MONTHNovember    -3.60       2.66   -1.35  0.18023    
## SITUATIONS3:MONTHNovember    -2.40       2.66   -0.90  0.37000    
## SITUATIONS4:MONTHNovember    -1.60       2.66   -0.60  0.54946    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.21 on 72 degrees of freedom
## Multiple R-squared:  0.64,	Adjusted R-squared:  0.605 
## F-statistic: 18.3 on 7 and 72 DF,  p-value: 9.55e-14

anova(starling.lm)

## Analysis of Variance Table
## 
## Response: MASS
##                 Df Sum Sq Mean Sq F value  Pr(>F)    
## SITUATION        3    574     191   10.82 6.0e-06 ***
## MONTH            1   1656    1656   93.60 1.2e-14 ***
## SITUATION:MONTH  3     34      11    0.64    0.59    
## Residuals       72   1274      18                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
and fill in the following table:
Source of VariationSSdfMSF-ratioPvalue
SITUATION
MONTH
SITUATION : MONTH
Residual (within groups)   

Q2-4.An interaction plot (plot of means)
is useful for summarizing multi-way ANOVA models. Summarize the trends using an interaction plot (HINT).
Show code
library(car)

## Loading required package: MASS

## Loading required package: nnet

with(starling, interaction.plot(SITUATION, MONTH, MASS))
plot of chunk Q2-4

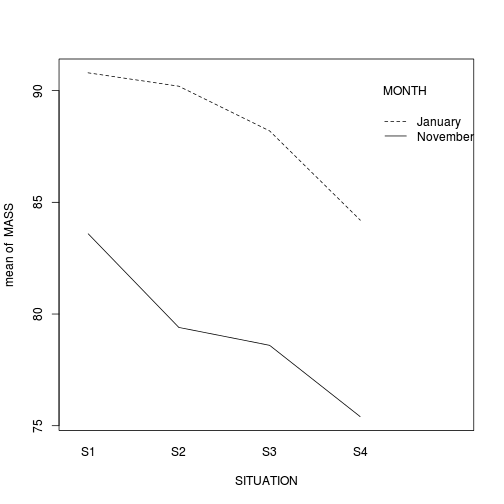
In the classical frequentist regime, many at this point would advocate dropping the interaction term from the model (p-value for the interaction is greater than 0.25). This term is not soaking up much of the residual and yet is soaking up 3 degrees of freedom. The figure also indicates that situation and month are likely to operate additively.

Q2-5. In the absence of an interaction, we can examine the effects of each of the main effects in isolation. It is not necessary to examine the effect of MONTH any further, as there were only two groups. However, if we wished to know which roosting situations were significantly different to one another, we need to perform additional multiple comparisons
. Since we don't know anything about the roosting situations, no one comparison is any more or less meaningful than any other comparisons. Therefore, a Tukey's test is most appropriate. Perform a Tukey's test (HINT)
and summarize indicate which of the following comparisons were significant (put * in the box to indicate P< 0.05, ** to indicate P< 0.001, and NS to indicate not-significant).
Show code
library(multcomp)

## Loading required package: mvtnorm

## Loading required package: survival

## Loading required package: splines

summary(glht(starling.lm, linfct = mcp(SITUATION = "Tukey")))

## Warning: covariate interactions found -- default contrast might be inappropriate

## 
## 	 Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lm(formula = MASS ~ SITUATION * MONTH, data = starling)
## 
## Linear Hypotheses:
##              Estimate Std. Error t value Pr(>|t|)   
## S2 - S1 == 0    -0.60       1.88   -0.32   0.9887   
## S3 - S1 == 0    -2.60       1.88   -1.38   0.5146   
## S4 - S1 == 0    -6.60       1.88   -3.51   0.0043 **
## S3 - S2 == 0    -2.00       1.88   -1.06   0.7129   
## S4 - S2 == 0    -6.00       1.88   -3.19   0.0112 * 
## S4 - S3 == 0    -4.00       1.88   -2.13   0.1545   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

library(multcomp)
summary(glht(lm(MASS ~ SITUATION + MONTH, data = starling), linfct = mcp(SITUATION = "Tukey")))

## 
## 	 Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lm(formula = MASS ~ SITUATION + MONTH, data = starling)
## 
## Linear Hypotheses:
##              Estimate Std. Error t value Pr(>|t|)    
## S2 - S1 == 0    -2.40       1.32   -1.82   0.2735    
## S3 - S1 == 0    -3.80       1.32   -2.88   0.0263 *  
## S4 - S1 == 0    -7.40       1.32   -5.60   <0.001 ***
## S3 - S2 == 0    -1.40       1.32   -1.06   0.7147    
## S4 - S2 == 0    -5.00       1.32   -3.79   0.0018 ** 
## S4 - S3 == 0    -3.60       1.32   -2.73   0.0388 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

confint(glht(lm(MASS ~ SITUATION + MONTH, data = starling), linfct = mcp(SITUATION = "Tukey")))

## 
## 	 Simultaneous Confidence Intervals
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lm(formula = MASS ~ SITUATION + MONTH, data = starling)
## 
## Quantile = 2.628
## 95% family-wise confidence level
##  
## 
## Linear Hypotheses:
##              Estimate lwr     upr    
## S2 - S1 == 0  -2.400   -5.870   1.070
## S3 - S1 == 0  -3.800   -7.270  -0.330
## S4 - S1 == 0  -7.400  -10.870  -3.930
## S3 - S2 == 0  -1.400   -4.870   2.070
## S4 - S2 == 0  -5.000   -8.470  -1.530
## S4 - S3 == 0  -3.600   -7.070  -0.130

ComparisonMultiplicativeAdditive
EstPLwrUprEstPLwrUpr
Situation 2 vs Situation 1
Situation 3 vs Situation 1
Situation 4 vs Situation 1
Situation 3 vs Situation 2
Situation 4 vs Situation 2
Situation 4 vs Situation 3

Q2-6.Using the additive model, fill out the following table of effect sizes and confidence intervals
Show code
starling.lm2 <- lm(MASS ~ SITUATION + MONTH, data = starling)
cbind(coef(starling.lm2), confint(starling.lm2))

##                       2.5 % 97.5 %
## (Intercept)   91.75  89.670 93.830
## SITUATIONS2   -2.40  -5.031  0.231
## SITUATIONS3   -3.80  -6.431 -1.169
## SITUATIONS4   -7.40 -10.031 -4.769
## MONTHNovember -9.10 -10.960 -7.240

contrasts(starling$SITUATION) <- contr.sum
EstimateMeanLower 95% CIUpper 95% CI
December Situation 1
Effect size (Dec:Sit2 - Dec:Sit1)
Effect size (Dec:Sit3 - Dec:Sit1)
Effect size (Dec:Sit4 - Dec:Sit1)
Effect size (Nov:Sit1 - Dec:Sit1)

Q2-7.Generate a bargraph to summarize the data
Show code
opar <- par(mar = c(5, 5, 1, 1))
star.means <- with(starling, tapply(MASS, list(MONTH, SITUATION), mean))
star.sds <- with(starling, tapply(MASS, list(MONTH, SITUATION), sd))
star.len <- with(starling, tapply(MASS, list(MONTH, SITUATION), length))
star.ses <- star.sds/sqrt(star.len)
xs <- barplot(star.means, ylim = range(starling$MASS), beside = T, axes = F, ann = F, axisnames = F, 
    xpd = F, axis.lty = 2, col = c(0, 1))
arrows(xs, star.means, xs, star.means + star.ses, code = 2, length = 0.05, ang = 90)
axis(2, las = 1)
axis(1, at = apply(xs, 2, median), lab = c("Situation 1", "Situation 2", "Situation 3", "Situation 4"))
mtext(2, text = "Mass (g) of starlings", line = 3, cex = 1.25)
legend("topright", leg = c("January", "November"), fill = c(0, 1), col = c(0, 1), bty = "n", cex = 1)
box(bty = "l")
plot of chunk Q2-7
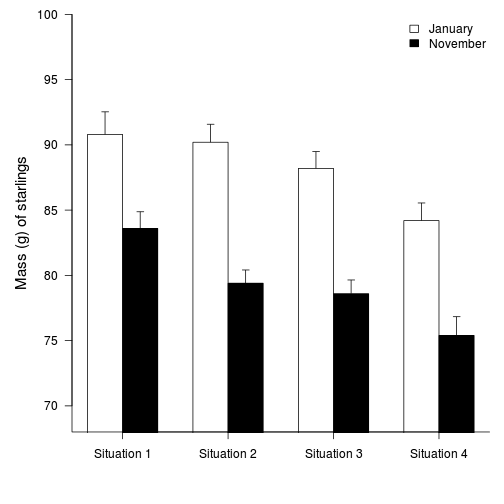
par(opar)

Q2-8. Summarize your conclusions from the analysis.

Exercise 3 - Two factor ANOVA - Type III SS

Here is a modified example from Quinn and Keough (2002). Stehman and Meredith (1995) present data from an experiment that was set up to test the hypothesis that healthy spruce seedlings break bud sooner than diseased spruce seedlings. There were 2 factors: pH (3 levels: 3, 5.5, 7) and HEALTH (2 levels: healthy, diseased). The dependent variable was the average (from 5 buds) bud emergence rating (BRATING) on each seedling. The sample size varied for each combination of pH and health, ranging from 7 to 23 seedlings. With two factors, this experiment should be analyzed with a 2 factor (2 x 3) ANOVA.

Download Stehman data set

Format of stehman.csv data files
PHHEALTHGROUPBRATING
3DD30.0
........
3HH30.8
........
5.5DD5.50.0
........
5.5HH5.50.0
........
7DD70.2
........

PHCategorical listing of pH (not however that the levels are numbers and thus by default the variable is treated as a numeric variable rather than a factor - we need to correct for this)
HEALTHCategorical listing of the health status of the seedlings, D = diseased, H = healthy
GROUPCategorical listing of pH/health combinations - used for checking ANOVA assumptions
BRATINGAverage bud emergence rating per seedling
Starlings

Open the stehman data file.

Show code
stehman <- read.table("../downloads/data/stehman.csv", header = T, sep = ",", strip.white = T)
head(stehman)

##   PH HEALTH GROUP BRATING
## 1  3      D    D3     0.0
## 2  3      D    D3     0.8
## 3  3      D    D3     0.8
## 4  3      D    D3     0.8
## 5  3      D    D3     0.8
## 6  3      D    D3     0.8

The variable PH contains a list of pH values and is supposed to represent a factorial variable. However, because the contents of this variable are numbers, R initially treats them as numbers, and therefore considers the variable to be numeric rather than categorical. In order to force R to treat this variable as a factor (categorical) it is necessary to first convert this numeric variable into a factor (HINT).
Show code
stehman$PH <- as.factor(stehman$PH)

Q3-1. Test the assumptions
by producing boxplots
and mean vs variance plot.

Show code
boxplot(BRATING ~ HEALTH * PH, data = stehman)
plot of chunk Q3-1
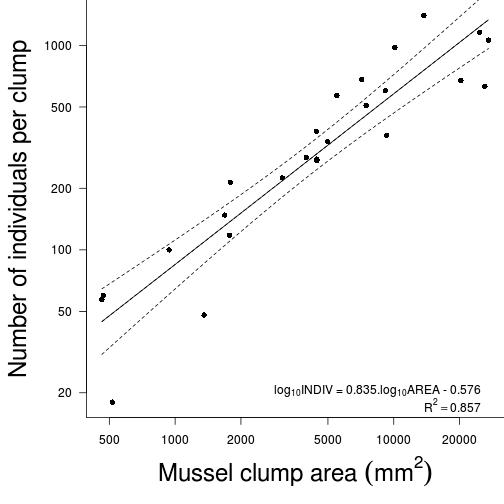
means <- with(stehman, tapply(BRATING, list(HEALTH, PH), mean))
vars <- with(stehman, tapply(BRATING, list(HEALTH, PH), var))
plot(means, vars, pch = 16)
plot of chunk Q3-1
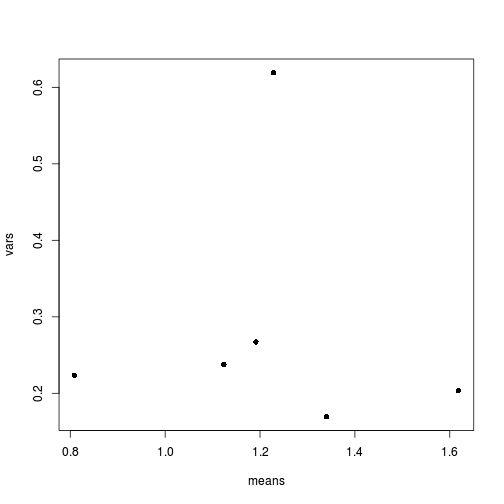
  1. Is there any evidence that one or more of the assumptions are likely to be violated? (Y or N)
  2. Is the proposed model balanced?
    (Y or N)
    3. Show code
    replications(BRATING ~ HEALTH * PH, data = stehman)

    ## $HEALTH
## HEALTH
##  D  H 
## 67 28 
## 
## $PH
## PH
##   3 5.5   7 
##  34  30  31 
## 
## $`HEALTH:PH`
##       PH
## HEALTH  3 5.5  7
##      D 23  23 21
##      H 11   7 10

    !is.list(replications(BRATING ~ HEALTH * PH, data = stehman))

    ## [1] FALSE

As the model is not balanced, we will likely want to examine the ANOVA table based on Type III (marginal) Sums of Squares. In preparation for doing so, we must define something other than treatment contrasts for the factors.

Show code
contrasts(stehman$HEALTH) <- contr.sum
contrasts(stehman$PH) <- contr.sum

Q3-2. Now fit a two-factor ANOVA model
and examine the residuals.
Any evidence of skewness or unequal variances? Any outliers? Any evidence of violations? ('Y' or 'N') . As the model is not balanced, we will base hypothesis tests on Type II sums of squares. Produce an ANOVA table (HINT) and fill in the following table:

Show code
stehman.lm <- lm(BRATING ~ HEALTH * PH, data = stehman)
library(car)
Anova(stehman.lm, type = "III")

## Anova Table (Type III tests)
## 
## Response: BRATING
##             Sum Sq Df F value Pr(>F)    
## (Intercept)  114.1  1  444.87 <2e-16 ***
## HEALTH         2.4  1    9.40 0.0029 ** 
## PH             1.9  2    3.63 0.0306 *  
## HEALTH:PH      0.2  2    0.37 0.6897    
## Residuals     22.8 89                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Source of VariationSSdfMSF-ratioPvalue
PH
HEALTH
PH : HEALTH
Residual (within groups)   

Q3-3.Summarize these trends using a interaction plot.
Show code
library(car)
with(stehman, interaction.plot(PH, HEALTH, BRATING))
plot of chunk Q3-3

Q3-4. In the absence of an interaction, we can examine the effects of each of the main effects in isolation. It is not necessary to examine the effect of HEALTH any further, as there were only two groups. However, if we wished to know which pH levels were significantly different to one another, we need to perform additional multiple comparisons.
Since no one comparison is any more or less meaningful than any other comparisons, a Tukey's test is most appropriate. Perform a Tukey's test
Show code
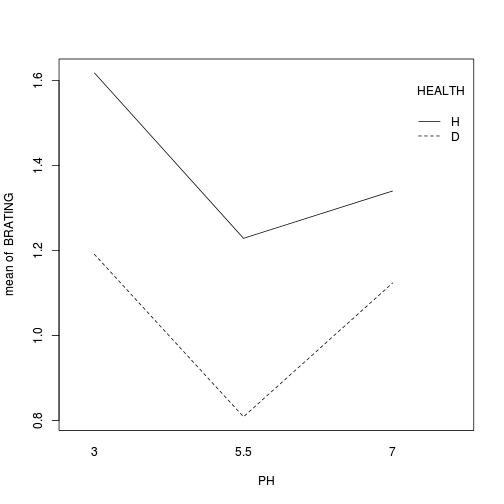
library(multcomp)
summary(glht(stehman.lm, linfct = mcp(PH = "Tukey")))

## Warning: covariate interactions found -- default contrast might be inappropriate

## 
## 	 Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lm(formula = BRATING ~ HEALTH * PH, data = stehman)
## 
## Linear Hypotheses:
##              Estimate Std. Error t value Pr(>|t|)  
## 5.5 - 3 == 0   -0.386      0.143   -2.69    0.023 *
## 7 - 3 == 0     -0.173      0.134   -1.29    0.407  
## 7 - 5.5 == 0    0.213      0.146    1.46    0.316  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)
and summarize indicate which of the following comparisons were significant (put * in the box to indicate P< 0.05, ** to indicate P< 0.001, and NS to indicate not-significant).
pH 3 vs pH 5.5
pH 3 vs pH 7
pH 5.5 vs pH 7

Q3-5.Generate a bargraph to summarize the findings of the above Tukey's test.

The above analysis reflects a very classic approach to investigating the effects of PH and HEALTH via NHST (null hypothesis testing). Many argue that a more modern/valid approach is to:

  1. Abandon hypothesis testing
  2. Estimate effect sizes and associated effect sizes
  3. As PH is an ordered factor, this is arguably better modelled via polynomial contrasts

Show code
stehman.lm2 <- lm(BRATING ~ PH * HEALTH, data = stehman, contrasts = list(PH = contr.poly(3, scores = c(3, 
    5.5, 7)), HEALTH = contr.treatment))
summary(stehman.lm2)

## 
## Call:
## lm(formula = BRATING ~ PH * HEALTH, data = stehman, contrasts = list(PH = contr.poly(3, 
##     scores = c(3, 5.5, 7)), HEALTH = contr.treatment))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.2286 -0.3238 -0.0087  0.3818  0.9913 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.0413     0.0619   16.81   <2e-16 ***
## PH.L          -0.0879     0.1077   -0.82   0.4162    
## PH.Q           0.2751     0.1069    2.57   0.0117 *  
## HEALTH2        0.3543     0.1155    3.07   0.0029 ** 
## PH.L:HEALTH2  -0.1360     0.1899   -0.72   0.4758    
## PH.Q:HEALTH2  -0.1008     0.2099   -0.48   0.6323    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.506 on 89 degrees of freedom
## Multiple R-squared:  0.196,	Adjusted R-squared:  0.15 
## F-statistic: 4.33 on 5 and 89 DF,  p-value: 0.00143

confint(stehman.lm2)

##                 2.5 % 97.5 %
## (Intercept)   0.91821 1.1643
## PH.L         -0.30184 0.1260
## PH.Q          0.06273 0.4875
## HEALTH2       0.12475 0.5839
## PH.L:HEALTH2 -0.51324 0.2413
## PH.Q:HEALTH2 -0.51773 0.3162

  1. Healthy spruce trees have a higher bud emergence rating than diseased (ES=0.35 CI=0.12-0.58)
  2. The bud emergence rating follows a quadratic change with PH

Q3-6. Summarize your biological conclusions from the analysis.

Q3-7. Why aren't the 5 buds from each tree true replicates? Given this, why bother observing 5 buds, why not just use one?

Exercise 4 - Two factor ANOVA

An ecologist studying a rocky shore at Phillip Island, in southeastern Australia, was interested in how clumps of intertidal mussels are maintained. In particular, he wanted to know how densities of adult mussels affected recruitment of young individuals from the plankton. As with most marine invertebrates, recruitment is highly patchy in time, so he expected to find seasonal variation, and the interaction between season and density - whether effects of adult mussel density vary across seasons - was the aspect of most interest.

The data were collected from four seasons, and with two densities of adult mussels. The experiment consisted of clumps of adult mussels attached to the rocks. These clumps were then brought back to the laboratory, and the number of baby mussels recorded. There were 3-6 replicate clumps for each density and season combination.

Download Quinn data set

Format of quinn.csv data files
SEASONDENSITYRECRUITSSQRTRECRUITSGROUP
SpringLow153.87SpringLow
..........
SpringHigh113.32SpringHigh
..........
SummerLow214.58SummerLow
..........
SummerHigh345.83SummerHigh
..........
AutumnLow143.74AutumnLow
..........
SEASONCategorical listing of Season in which mussel clumps were collected ­ independent variable
DENSITYCategorical listing of the density of mussels within mussel clump ­ independent variable
RECRUITSThe number of mussel recruits ­ response variable
SQRTRECRUITSSquare root transformation of RECRUITS - needed to meet the test assumptions
GROUPSCategorical listing of Season/Density combinations - used for checking ANOVA assumptions
Mussel

Open the quinn data file.

Show code
quinn <- read.table("../downloads/data/quinn.csv", header = T, sep = ",", strip.white = T)
head(quinn)

##   SEASON DENSITY RECRUITS SQRTRECRUITS      GROUP
## 1 Spring     Low       15        3.873  SpringLow
## 2 Spring     Low       10        3.162  SpringLow
## 3 Spring     Low       13        3.606  SpringLow
## 4 Spring     Low       13        3.606  SpringLow
## 5 Spring     Low        5        2.236  SpringLow
## 6 Spring    High       11        3.317 SpringHigh

Confirm the need for a square root transformation, by examining boxplots

and mean vs variance plots
for both raw and transformed data. Note that square root transformation was selected because the data were counts (count data often includes values of zero - cannot compute log of zero).

Show code
par(mfrow = c(2, 2))
boxplot(RECRUITS ~ SEASON * DENSITY, data = quinn)
means <- with(quinn, tapply(RECRUITS, list(SEASON, DENSITY), mean))
vars <- with(quinn, tapply(RECRUITS, list(SEASON, DENSITY), var))
plot(means, vars, pch = 16)
boxplot(SQRTRECRUITS ~ SEASON * DENSITY, data = quinn)
means <- with(quinn, tapply(SQRTRECRUITS, list(SEASON, DENSITY), mean))
vars <- with(quinn, tapply(SQRTRECRUITS, list(SEASON, DENSITY), var))
plot(means, vars, pch = 16)
plot of chunk Q4a

Also confirm that the design (model) is unbalanced
and thus warrants the use of Type III sums of squares. (HINT)
Show code
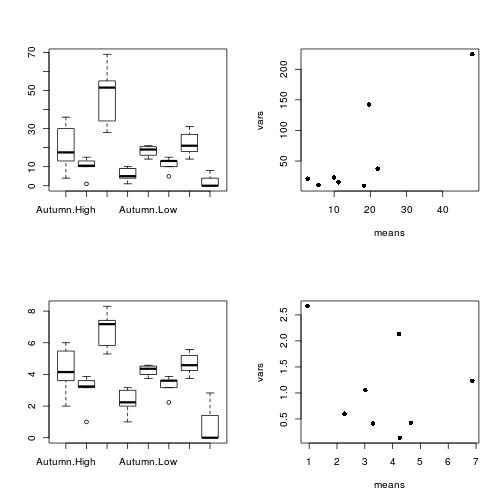
!is.list(replications(sqrt(RECRUITS) ~ SEASON * DENSITY, data = quinn))

## [1] FALSE

replications(sqrt(RECRUITS) ~ SEASON * DENSITY, data = quinn)

## $SEASON
## SEASON
## Autumn Spring Summer Winter 
##     10     11     12      9 
## 
## $DENSITY
## DENSITY
## High  Low 
##   24   18 
## 
## $`SEASON:DENSITY`
##         DENSITY
## SEASON   High Low
##   Autumn    6   4
##   Spring    6   5
##   Summer    6   6
##   Winter    6   3

contrasts(quinn$SEASON) <- contr.sum
contrasts(quinn$DENSITY) <- contr.sum

Q4-1. Now fit a two-factor ANOVA model
(using the square-root transformed data and examine the residuals.
Any evidence of skewness or unequal variances? Any outliers? Any evidence of violations? ('Y' or 'N')
. Produce an anova table based on Type III SS and fill in the following table:

Show code
quinn.lm <- lm(SQRTRECRUITS ~ SEASON * DENSITY, data = quinn)
library(car)
Anova(quinn.lm, type = "III")

## Anova Table (Type III tests)
## 
## Response: SQRTRECRUITS
##                Sum Sq Df F value  Pr(>F)    
## (Intercept)       540  1  529.04 < 2e-16 ***
## SEASON             91  3   29.61 1.3e-09 ***
## DENSITY             6  1    6.35   0.017 *  
## SEASON:DENSITY     11  3    3.71   0.021 *  
## Residuals          35 34                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Source of VariationSSdfMSF-ratioPvalue
SEASON
DENSITY
SEASON : DENSITY
Residual (within groups)   

Q4-2.Summarize these trends using a interaction plot.
Note that graphs do not place the restrictive assumptions on data sets that formal analyses do (since graphs are not statistical analyses). Therefore, it data transformations were used for the purpose of meeting test assumptions, it is usually better to display raw data (non transformed) in graphical presentations. This way readers can easily interpret actual values in a scale that they are more familiar with.
Show code
library(car)
with(quinn, interaction.plot(SEASON, DENSITY, SQRTRECRUITS))
plot of chunk Q4-2

Q4-3. The presence of a significant interaction means that we cannot make general statements about the effect of one factor (such as density) in isolation of the other factor (e.g. season). Whether there is an effect of density depends on which season you are considering (and vice versa). One way to clarify an interaction is to analyze subsets of the data. For example, you could examine the effect of density separately at each season (using four, single factor ANOVA's), or analyze the effect of season separately (using two, single factor ANOVA's) at each mussel density.
For the current data set, the effect of density is of greatest interest, and thus the former option is the most interesting. Perform the simple main effects anovas.

Download biology package

Show code
library(biology)
AnovaM(quinn.lm.summer <- mainEffects(quinn.lm, at = SEASON == "Summer"), type = "III")

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## INT          6   91.2   15.20    14.9 2.8e-08 ***
## DENSITY      1   14.7   14.70    14.4 0.00058 ***
## Residuals   34   34.7    1.02                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

library(biology)
AnovaM(quinn.lm. <- mainEffects(quinn.lm, at = SEASON == "Autumn"), type = "III")

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## INT          6  105.9   17.65    17.3 4.7e-09 ***
## DENSITY      1    0.0    0.00     0.0    0.96    
## Residuals   34   34.7    1.02                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

AnovaM(quinn.lm. <- mainEffects(quinn.lm, at = SEASON == "Winter"), type = "III")

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## INT          6  102.4   17.06   16.72 7.1e-09 ***
## DENSITY      1    3.5    3.54    3.47   0.071 .  
## Residuals   34   34.7    1.02                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

AnovaM(quinn.lm. <- mainEffects(quinn.lm, at = SEASON == "Spring"), type = "III")

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

## Warning: number of items to replace is not a multiple of replacement length

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## INT          6  105.7   17.61    17.3 4.8e-09 ***
## DENSITY      1    0.2    0.21     0.2    0.65    
## Residuals   34   34.7    1.02                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

  1. Was the effect of DENSITY on recruitment consistent across all levels of SEASON? (Y or N)
  2. How would you interpret these results?
  Nested ANOVA

A nested ANOVA is a simple extension of the single factor ANOVA. An additional factor (Factor B) is added that is nested within the main factor of interest (Factor A). Nested factors are incorporated in situations where researches envisage potentially large amounts of variation between different sets of replicates within the main Factor.
For example, a limnologist investigating the effect of flow (Factor A: high, medium and low) on macroinvertebate density, might collect samples from a number of high, medium and low flow streams. However, the limnologist might expect that many other factors (perhaps more important than stream flow) also influence the density of macroinvertebrates and that even samples collected in close proximity to one another might be expected to vary considerably in density of macroinvertebrates. Such variability increases the unexplained variability and therefore has the potential to make it very difficult to pick up the effect of the actual factor of interest (in this case flow).
In an attempt to combat this, the researcher decides to collect multiple samples from within each stream. If some of the unexplained variability can be explained by variation between samples within streams, then the test of flow will be more sensitive.
This is called a nested ANOVA, an additional factor (Factor B: stream) has been introduce within the main factor (Factor A: flow). Factor A is a fixed factor as we are only interested in the specific levels chosen (e.g. high, medium and low flow). Factor B however, is a random as we are not just interested in the specific streams that were sampled, we are interested in all the possible streams that they represent. In a nested ANOVA the categories of the Factor B nested within each level of Factor A are different. E.g. the streams used for each flow type are different. Therefore it is not possible to test for an interaction between Flow type and stream.

There are two null hypotheses being tested in a two factor nested ANOVA. H0 main effect: no effect of Factor A (flow) H0: = &mu1 = &mu2 = ... = &mui = &mu (as for single factor ANOVA). H0 nesting effect: no effect of Factor B (stream) nested within Factor A (flow). Technically it is that there is no added variance due to differences between all the possible levels of Factor B with any level of Factor A. E.g., that there is no added variance due to differences between all possible high flow streams, or between all possible medium flow streams or between all possible low flow streams. Diagram shows layout of nested design with three treatments (different pattern fills).

End of instructions

  Two factor ANOVA

Statistical models that incorporate more than one categorical predictor variable are broadly referred to as multivariate analysis of variance. There are two main reasons for the inclusion of multiple factors:

  1. To attempt to reduce the unexplained (or residual) variation in the response variable and therefore increase the sensitivity of the main effect test.
  2. To examine the interaction between factors. That is, whether the effect of one factor on the response variable is dependent on other factor(s) (consistent across all levels of other factor(s)).

Fully factorial linear models are used when the design incorporates two or more factors (independent, categorical variables) that are crossed with each other. That is, all combinations of the factors are included in the design and every level (group) of each factor occurs in combination with every level of the other factor(s). Furthermore, each combination is replicated.

In fully factorial designs both factors are equally important (potentially), and since all factors are crossed, we can also test whether there is an interaction between the factors (does the effect of one factor depend on the level of the other factor(s)). Graphs above depict a) interaction, b) no interaction.


For example, Quinn (1988) investigated the effects of season (two levels, winter/spring and summer/autumn) and adult density (four levels, 8, 15, 30 and 45 animals per 225cm2) on the number of limpet egg masses. As the design was fully crossed (all four densities were used in each season), he was also able to test for an interaction between season and density. That is, was the effect of density consistent across both seasons and, was the effect of season consistent across all densities.

Diagram shows layout of 2 factor fully crossed design. The two factors (each with two levels) are color (black or gray) and pattern (solid or striped). There are three experimental units (replicates) per treatment combination.


End of instructions

  Reading data into R

Ensure that the working directory is pointing to the path containing the file to be imported before proceeding.
To import data into R, we read the contents of a file into a data frame. The general format of the command for reading data into a data frame is

> name <- read.table('filename.csv', header=T, sep=',', row.names=column, strip.white=T)

where name is a name you wish the data frame to be referred to as, filename.csv is the name of the csv file that you created in excel and column is the number of the column that had row labels (if there were any). The argument header=T indicates that the variable (vector) names will be created from the names supplied in the first row of the file. The argument sep=',' indicates that entries in the file are separated by a comma (hence a comma delimited file). If the data file does not contain row labels, or you are not sure whether it does, it is best to omit the row.names=column argument. The strip.white=T arguement ensures that no leading or trailing spaces are left in character names (these can be particularly nasty in categorical variables!).

As an example 
phasmid <- read.data("phasmid.csv", header = T, sep = ",", row.names = 1, strip.white = T)

End of instructions

  Convert numeric variable into a factor

> data$var <- as.factor(data$var)

where data is the name of the data set and var is the name of the variable to be made into a factor. While there is no visible evidence that the data are any different, R will now treat the variable as a factor rather than as a numeric variable.

End of instructions

  Nested ANOVA assumptions

In ANOVA, the assumptions of normality and variance homogeneity apply to the residuals for the test of interest. In this example, the nested factor (Factor B, SITE) is random. Therefore, the normality and heterogeneity of variance assumptions for Factor A (SEASON) must be based on the distribution, mean and variance of the response variable (S4DUGES) for each level of Factor A using the means of Factor B within each Factor A as the observations (since the error term for Factor A (SEASON) is the variation in the response variable between categories of Factor B within each level of Factor A (MSSITE). Calculate the mean from each level of Factor B (SITE), and use these means to calculate the mean, variance and distribution of each level of Factor A (SEASON).

# aggregate the data set by calculating the means for each level of the nesting factor
> name.ag <- aggregate(dataset, list(Name1=FactorA, Name2=FactorB), mean)
#OR perhaps more efficiently
library(lme4)
name.ag &ly- gsummary(dataset, groups=FactorB)
# use the aggregated means to produce the boxplots
> boxplot(dv~FactorA, name.ag)

where name.ag is a name given to the new aggregated data set, dataset is the name of the original data set, Name1 and Name2 are names to appear in the aggregated data set that represent FactorA (Main within factor) and FactorB (nesting factor) respectively. Finally, dv is the name of the dependent variable.

This data set generates two boxplots, each constructed from only 3 values and thus of questionable value.

End of instructions

  Nested ANOVA assumptions

# fit the heirachical linear model
> name.aov <- aov(dv~FactorA + Error(FactorB), data=data)
# print out the ANOVA strata
> summary(name.aov)

where name.aov is a name provided to store the fitted model, dv is the dependent variable, FactorA is the main fixed factor and FactorB is the random nested factor. data is the name of the data set. The 'Error()' argument defines additional error (residual) strata, hence the above template indicates that Factor should be tested against FactorB.
For example:

# fit the heirachical linear model
> curdies.aov <- aov(S4DUGES~SEASON + Error(SITE), data=curdies)
# print out the ANOVA strata
> summary(curdies.aov)

In recognition that Factor is a random nested factor, and thus of little interest, the F-ratio is not provided. Since the effect of FactorB is tested against the overal residual (error) term, to obtain the F-ratio for the test of FactorB, fit the model without defining the an additional error strata. Note that when you do this, all terms are tested against the residual term and therefore, any fixed factors above the random factors (in the hierarchy) will be incorrectly calculated.

> curdies.aov1 <- aov(S4DUGES~SEASON + SITE, data=curdies)
> summary(curdies.aov)

End of instructions

  Two-factor ANOVA

> name.aov <- aov(dv~factor1 * factor2, data=data)

where dv is the name of the numeric vector (dependent variable), factor1 and factor2 are the names of the factors (categorical or factor variables) and data is the name of the data frame (data set).

End of instructions

  Fully factorial ANOVA assumption checking

The assumptions of normality and homogeneity of variance apply to each of the factor level combinations, since it is the replicate observations of these that are the test residuals. If the design has two factors (IV1 and IV2) with three and four levels (groups) respectively within these factors, then a boxplot of each of the 3x4=12 combinations needs to be constructed. It is recommended that a variable (called GROUP) be setup to represent the combination of the two categorical (factor) variables.

Simply construct a boxplot with the dependent variable on the y-axis and GROUP on the x-axis. Visually assess whether the data from each group is normal (or at least that the groups are not all consistently skewed in the same direction), and whether the spread of data is each group is similar (or at least not related to the mean for that group). The GROUP variable can also assist in calculating the mean and variance for each group, to further assess variance homogeneity.

End of instructions

  Factorial boxplots

> boxplot(dv~factor1*factor2,data=data)

where dv is the name of the numeric vector (dependent variable), factor1 and factor2 are the names of the factors (categorical or factor variables) and data is the name of the data frame (data set). The '~' is used in formulas to represent that the left hand side is proportional to the right hand side.

End of instructions

  Plotting mean vs variance

# first calculate the means and variances
> means <- tapply(data$dv, list(data$factor1, data$factor2), mean)
> vars <- tapply(data$dv, list(data$factor1, data$factor2), var)
# then plot the mean against variance
> plot(means,vars)

where dv is the name of the numeric vector (dependent variable), factor1 and factor2 are the names of the factors (categorical or factor variables) and data is the name of the data frame (data set).

End of instructions

  Model balance

Balanced models are those models that have equal sample sizes for each level of a treatment. Unequal sample sizes are generally problematic for statistical analyses as they can be the source of unequal variances. They are additionally problematic for multifactor designs because of the way that total variability is partitioned into the contributions of each of the main effects as well as the contributions of interactions (ie the calculations of sums of squares and degrees of freedom). Sums of squares (and degrees of freedom) are usually (type I SS) partitioned additively. That is:
SSTotal=SSA+SSB+SSAB+SSResidual, and
dfTotal=dfA+dfB+dfAB+dfResidual
. In practice, these formulas are used in reverse. For example, if the model was entered as DV~A+B+AB, first SSResidual is calculated followed by SSAB, then SSB. SSA is thus calculated as the total sums of squares minus what has already been partitioned off to other terms (SSA=SSTotal-SSB+SSAB+SSResidual). If the model is balanced, then it doesn't matter what order the model is constructed (DV~B+A+AB will be equivalent).

However, in unbalanced designs, SS cannot be partitioned additively, that is the actual SS of each of the terms does not add up to SSTotal (SSTotal=SSA+SSB+SSAB+SSResidual). Of course, when SS is partitioned it all must add up. Consequently, the SS of the last term to be calculated will not be correct. Therefore, in unbalanced designs, SS values for the terms are different (and therefore so are the F-ratios etc) depending on the order in which the terms are added - an undesirable situation.

To account for this, there are alternative methods of calculating SS for the main effects (all provide same SS for interaction terms and residuals).

It turns out that it is relatively easy to determine whether or not the model is balanced or not - use the following syntax:

> !is.list(replications(formula,data))

where formula is the model formula (for example, MASS~SITUATION*MONTH) and data is the name of data set.
If this function returns a TRUE, your model is balanced. If it returns a FALSE then your model is not balanced and you should consider using Type II or III SS methods.

End of instructions

  Linear regression diagnostics

> plot(name.lm)

where name.lm is the name of a fitted linear model. You will be prompted to hit return to cycle through a series of four diagnostic plots. The first (and most important of these) is the Residual Plot.

End of instructions

  ANOVA table

#print a summary of the ANOVA table
> anova(name.aov)

where name.aov is the name of a fitted linear model.

End of instructions

  Interaction plot

Interaction plots display the degree of consistency (or lack of) of the effect of one factor across each level of another factor. Interaction plots can be either bar or line graphs, however line graphs are more effective. The x-axis represents the levels of one factor, and a separate line in drawn for each level of the other factor. The following interaction plots represent two factors, A (with levels A1, A2, A3) and B (with levels B1, B2).


The parallel lines of first plot clearly indicate no interaction. The effect of factor A is consistent for both levels of factor B and visa versa. The middle plot demonstrates a moderate interaction and bottom plot illustrates a severe interaction. Clearly, whether or not there is an effect of factor B (e.g. B1 > B2 or B2 > B1) depends on the level of factor A. The trend is not consistent.

End of instructions

  R Interaction plot

> interaction.plot(dataset$Factor1, dataset$Factor2, dataset$dv)

where Factor1 is the name of the categical variable (factor) with the most levels (this will be used for the x-axis), Factor2 is the name of the other factorial variable (this will be used to produce the different lines) and dv is the name of the dependent variable within the dataset data set
For example:

> interaction.plot(copper$DIST, copper$COPPER, dataset$WORMS)

End of instructions

  Specific comparisons of means

Following a significant ANOVA result, it is often desirable to specifically compare group means to determine which groups are significantly different. However, multiple comparisons lead to two statistical problems. Firstly, multiple significance tests increase the Type I errors (&alpha, the probability of falsely rejecting H0). E.g., testing for differences between 5 groups requires ten pairwise comparisons. If the &alpha for each test is 0.05 (5%), then the probability of at least one Type I error for the family of 10 tests is 0.4 (40%). Secondly, the outcome of each test needs to be independent (orthogonality). E.g. if A>B and B>C then we already know the result of A vs. C.

Post-hoc unplanned pairwise comparisons (e.g. Tukey's test) compare all possible pairs of group means and are useful in an exploratory fashion to reveal major differences. Tukey's test control the family-wise Type I error rate to no more that 0.05. However, this reduces the power of each of the pairwise comparisons, and only very large differences are detected (a consequence that exacerbates with an increasing number of groups).

Planned comparisons are specific comparisons that are usually planned during the design stage of the experiment. No more than (p-1, where p is the number of groups) comparisons can be made, however, each comparison (provided it is non-orthogonal) can be tested at &alpha = 0.05. Amongst all possible pairwise comparisons, specific comparisons are selected, while other meaningless (within the biological context of the investigation) are ignored.

Planned comparisons are defined using what are known as contrasts coefficients. These coefficients are a set of numbers that indicate which groups are to be compared, and what the relative contribution of each group is to the comparison. For example, if a factor has four groups (A, B, C and D) and you wish to specifically compare groups A and B, the contrast coefficients for this comparison would be 1, -1, 0,and 0 respectively. This indicates that groups A and B are to be compared (since their signs oppose) and that groups C and D are omitted from the specific comparison (their values are 0).

It is also possible to compare the average of two or more groups with the average of other groups. For example, to compare the average of groups A and B with the average of group C, the contrast coefficients would be 1, 1, -2, and 0 respectively. Note that 0.5, 0.5, 1 and 0 would be equivalent.

The following points relate to the specification of contrast coefficients:

  1. The sum of the coefficients should equal 0
  2. Groups to be compared should have opposing signs

End of instructions

  Tukey's Test

# load the 'multcomp' package
> library(multcomp)
# perform Tukey's test
> summary(simtest(dv~factor1*factor2, whichf='factor', data=data, type="Tukey"))
# OR the more up to date method
> summary(glht(data.aov, linfct=mcp(factor="Tukey")))

where dv is the name of the numeric vector (dependent variable), factor1 and factor2 are the names of the factors (categorical or factor variables), and data is the name of the data frame (data set). The argument tyoe="Tukey" indicates that a Tukeys p-value adjustments should be made. When the linear model contains multiple categorical predictor variables, the arguement whichf='' must be used to indicate which factor the Tukey's test should be performed on.

The coefficients list the specific comparisons made. Each line represents a specific hypothesis test including difference between groups, t-value, raw p value and Tukey's adjusted p value (the other values presented are not important for BIO3011).

End of instructions

  Simple Main Effects

> library(biology)
> quinn.aov1 <- aov(SQRTRECRUITS~DENSITY, data=quinn, subset=c(SEASON=='Summer'))
> AnovaM(lm(quinn.aov1), lm(quinn.aov),type="II")

Subset, type in the name of the other categorical variable followed by == (two equals signs) and the name of one of the levels (surrounded by single quotation marks) of this factor. For example, if you had a categorical variable called TEMPERATURE and it consisted of three levels (High, Medium and Low), to perform a anova using only the High temperature data, the subset expression would be TEMPERATURE=='High'.

End of instructions