Workshop 9.5a - Analysis of covariance (ANCOVA)
23 April 2011
ANCOVA references
- McCarthy (2007) - Chpt 6
- Kery (2010) - Chpt 10
- Gelman & Hill (2007) - Chpt 4
- Logan (2010) - Chpt 12
- Quinn & Keough (2002) - Chpt 9
library(R2jags)
library(ggplot2) library(grid) #define my common ggplot options murray_opts <- opts(panel.grid.major=theme_blank(), panel.grid.minor=theme_blank(), panel.border = theme_blank(), panel.background = theme_blank(), axis.title.y=theme_text(size=15, vjust=0,angle=90), axis.text.y=theme_text(size=12), axis.title.x=theme_text(size=15, vjust=-1), axis.text.x=theme_text(size=12), axis.line = theme_segment(), legend.position=c(1,0.1),legend.justification=c(1,0), legend.key=theme_blank(), plot.margin=unit(c(0.5,0.5,1,2),"lines") )
#create a convenience function for predicting from mcmc objects predict.mcmc <- function(mcmc, terms=NULL, mmat, trans="identity") { library(plyr) library(coda) if(is.null(terms)) mcmc.coefs <- mcmc else { iCol<-match(terms, colnames(mcmc)) mcmc.coefs <- mcmc[,iCol] } t2=")" if (trans=="identity") { t1 <- "" t2="" }else if (trans=="log") { t1="exp(" }else if (trans=="log10") { t1="10^(" }else if (trans=="sqrt") { t1="(" t2=")^2" } eval(parse(text=paste("mcmc.sum <-adply(mcmc.coefs %*% t(mmat),2,function(x) { data.frame(mean=",t1,"mean(x)",t2,", median=",t1,"median(x)",t2,", ",t1,"coda:::HPDinterval(as.mcmc(x), p=0.68)",t2,", ",t1,"coda:::HPDinterval(as.mcmc(x))",t2," )})", sep=""))) mcmc.sum } #create a convenience function for summarizing mcmc objects summary.mcmc <- function(mcmc, terms=NULL, trans="identity") { library(plyr) library(coda) if(is.null(terms)) mcmc.coefs <- mcmc else { iCol<-grep(terms, colnames(mcmc)) mcmc.coefs <- mcmc[,iCol] } t2=")" if (trans=="identity") { t1 <- "" t2="" }else if (trans=="log") { t1="exp(" }else if (trans=="log10") { t1="10^(" }else if (trans=="sqrt") { t1="(" t2=")^2" } eval(parse(text=paste("mcmc.sum <-adply(mcmc.coefs,2,function(x) { data.frame(mean=",t1,"mean(x)",t2,", median=",t1,"median(x)",t2,", ",t1,"coda:::HPDinterval(as.mcmc(x), p=0.68)",t2,", ",t1,"coda:::HPDinterval(as.mcmc(x))",t2," )})", sep=""))) mcmc.sum$Perc <-100*mcmc.sum$median/sum(mcmc.sum$median) mcmc.sum }
Homogeneous slopes
To investigate the impacts of sexual activity on the fruitfly longevity, Partridge and Farquhar (1981), measured the longevity of male fruitflies with access to either one virgin female (potential mate), eight virgin females, one pregnant female (not a potential mate), eight pregnant females or no females. The pool of available male fruitflies varied in size and since size is known to impact longevity, the researchers also measured thorax length as a covariate.
Download Partridge1 data set| Format of partridge1.csv data file | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Open the partridge1 data file. HINT.
partridge <- read.table("../downloads/data/partridge1.csv", header = T, sep = ",", strip.white = T) head(partridge)
## TREATMENT THORAX LONGEV ## 1 Preg8 0.64 35 ## 2 Preg8 0.68 37 ## 3 Preg8 0.68 49 ## 4 Preg8 0.72 46 ## 5 Preg8 0.72 63 ## 6 Preg8 0.76 39
- In the table below, list the assumptions of nested ANOVA along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
Assumption Diagnostic/Risk Minimization I. II. III. IV. V. -
Check the assumptions of normality and homogeneity of variances (HINT).
Is there any evidence of violations of the assumptions? (Y or N)
If so, assess whether a transformation will address the violations (HINT).View full codeplot(aov(LONGEV ~ THORAX + TREATMENT, partridge), which = 1)

-
Check these assumptions of linearity and homogeneity of slopes EMPIRICALLY (HINT).
Is there any evidence of violations of the assumptions? (Y or N)
View full codeanova(aov(log10(LONGEV) ~ THORAX * TREATMENT, partridge))
## Analysis of Variance Table ## ## Response: log10(LONGEV) ## Df Sum Sq Mean Sq F value Pr(>F) ## THORAX 1 1.212 1.212 176.50 <2e-16 *** ## TREATMENT 4 0.783 0.196 28.50 <2e-16 *** ## THORAX:TREATMENT 4 0.043 0.011 1.56 0.19 ## Residuals 115 0.790 0.007 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
- Finally,
check that the ranges of the covariate are similar for each level
of
the
categorical variable
(HINT).
Is there any evidence that the ranges of the covariate differ between the
different
levels
of
the
categorical
variable? (Y or N)
View full codeanova(aov(THORAX ~ TREATMENT, partridge))
## Analysis of Variance Table ## ## Response: THORAX ## Df Sum Sq Mean Sq F value Pr(>F) ## TREATMENT 4 0.030 0.00750 1.26 0.29 ## Residuals 120 0.714 0.00595
- In addition to the global Ancova, the researchers likely
to have been interested in examining a set of specific planned
comparisons. Two such contrasts could be:
- "pregnant versus virgin partners (to investigate the impacts of any sexual activity)?" (contrast coefficients: 0, .5, .5, -.5, -.5)
- "one virgin versus eight virgin partners (to investigate the impacts of sexual frequency)?" (contrast coefficients: 0, 0, 0, 1, -1)
- Before we fit the
linear model (perform the ANOVA), we need to define the contrast
coefficients (and thus comparisons) that we wish to perform in addition
to the global ANOVA. Define
the contrasts for the TREATMENT variable
(HINT)
View full code
contrasts(partridge$TREATMENT) <- cbind(c(0, 0.5, 0.5, -0.5, -0.5), c(0, 0, 0, 1, -1)) round(crossprod(contrasts(partridge$TREATMENT)), 1)
## [,1] [,2] [,3] [,4] ## [1,] 1 0 0 0 ## [2,] 0 2 0 0 ## [3,] 0 0 1 0 ## [4,] 0 0 0 1
- If there is no evidence that the assumptions have been violated and the contrasts were successfully defined, run the linear model, check residuals and examine the ANOVA table
View full code
library(biology) AnovaM(aov(log10(LONGEV) ~ THORAX + TREATMENT, partridge), split = list(TREATMENT = list(`Preg vs Virg` = 1, `1 Virg vs * Virg` = 2)), type = "III")
## Warning: number of items to replace is not a multiple of replacement length
## Df Sum Sq Mean Sq F value Pr(>F) ## THORAX 1 1.017 1.017 145.4 < 2e-16 *** ## TREATMENT 4 0.783 0.196 28.0 2.2e-16 *** ## TREATMENT: Preg vs Virg 1 0.542 0.542 77.5 1.3e-14 *** ## TREATMENT: 1 Virg vs * Virg 1 0.199 0.199 28.5 4.6e-07 *** ## Residuals 119 0.833 0.007 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
View full code for glslibrary(nlme) partridge.lme <- gls(log10(LONGEV) ~ THORAX + TREATMENT, partridge) anova(partridge.lme, type = "marginal")
## Denom. DF: 119 ## numDF F-value p-value ## (Intercept) 1 85.73 <.0001 ## THORAX 1 145.43 <.0001 ## TREATMENT 4 27.97 <.0001
summary(partridge.lme)## Generalized least squares fit by REML ## Model: log10(LONGEV) ~ THORAX + TREATMENT ## Data: partridge ## AIC BIC logLik ## -220.8 -201.3 117.4 ## ## Coefficients: ## Value Std.Error t-value p-value ## (Intercept) 0.7557 0.08162 9.259 0.0000 ## THORAX 1.1939 0.09900 12.060 0.0000 ## TREATMENT1 0.1473 0.01673 8.802 0.0000 ## TREATMENT2 0.0639 0.01197 5.338 0.0000 ## TREATMENT3 -0.0259 0.01674 -1.545 0.1250 ## TREATMENT4 -0.0314 0.01686 -1.860 0.0654 ## ## Correlation: ## (Intr) THORAX TREATMENT1 TREATMENT2 TREATMENT3 ## THORAX -0.996 ## TREATMENT1 -0.019 0.019 ## TREATMENT2 0.155 -0.155 -0.003 ## TREATMENT3 0.032 -0.033 -0.001 0.005 ## TREATMENT4 -0.124 0.125 0.002 -0.019 -0.004 ## ## Standardized residuals: ## Min Q1 Med Q3 Max ## -2.71075 -0.69874 -0.04147 0.71687 2.03709 ## ## Residual standard error: 0.08364 ## Degrees of freedom: 125 total; 119 residual
- Present the results of the planned comparisons as part of the following ANOVA table:
Source of Variation SS df MS F-ratio Pvalue THORAX TREATMENT Preg vs Virg 1 Virg vs 8 Virg Residual (within groups)
Fit the linear model and produce an ANOVA table to test the null hypotheses that there no effects of treatment (female type) on the (log transformed) longevity of male fruitflies adjusted for thorax length. Note that as the design is inherently imbalanced (since there is a different series of thorax lengths within each treatment type), Type I sums of squares are inappropriate. Therefore Type III sums of squares will be used.
Heterogeneous slopes
Constable (1993) compared the inter-radial suture widths of urchins maintained on one of three food regimes (Initial: no additional food supplied above what was in the initial sample, low: food supplied periodically and high: food supplied ad libitum. In an attempt to control for substantial variability in urchin sizes, the initial body volume of each urchin was measured as a covariate.
Download Partridge1 data set| Format of constable.csv data file | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Open the constable data file. HINT.
constable <- read.table("../downloads/data/constable.csv", header = T, sep = ",", strip.white = T) head(constable)
## TREAT IV SUTW ## 1 Initial 3.5 0.010 ## 2 Initial 5.0 0.020 ## 3 Initial 8.0 0.061 ## 4 Initial 10.0 0.051 ## 5 Initial 13.0 0.041 ## 6 Initial 13.0 0.061
-
In the table below, list the assumptions of nested ANOVA along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
Assumption Diagnostic/Risk Minimization I. II. III. IV. V. -
Check the assumptions of normality and homogeneity of variances (HINT).
Is there any evidence of violations of the assumptions? (Y or N) View full code
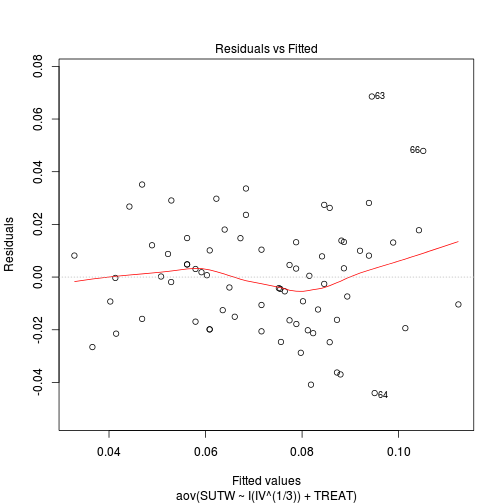
plot(aov(SUTW ~ I(IV^(1/3)) + TREAT, constable), which = 1)
-
Check these assumptions of linearity and homogeneity of slopes GRAPHICALLY (HINT).
Is there any evidence of violations of the assumptions? (Y or N) View full code
library(car) scatterplot(SUTW ~ I(IV^(1/3)) | TREAT, constable)

-
Check these assumptions of linearity and homogeneity of slopes EMPIRICALLY (HINT).
Is there any evidence of violations of the assumptions? (Y or N) View full code
anova(aov(SUTW ~ I(IV^(1/3)) * TREAT, constable))
## Analysis of Variance Table ## ## Response: SUTW ## Df Sum Sq Mean Sq F value Pr(>F) ## I(IV^(1/3)) 1 0.00654 0.00654 15.6 0.00019 *** ## TREAT 2 0.01675 0.00838 20.0 1.7e-07 *** ## I(IV^(1/3)):TREAT 2 0.00394 0.00197 4.7 0.01234 * ## Residuals 66 0.02769 0.00042 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
-
Finally,
check that the ranges of the covariate are similar for each level
of
the
categorical variable
(HINT).
Is there any evidence that the ranges of the covariate differ between the
different
levels
of
the
categorical
variable? (Y or N) View full code
anova(aov(I(IV^(1/3)) ~ TREAT, constable))
## Analysis of Variance Table ## ## Response: I(IV^(1/3)) ## Df Sum Sq Mean Sq F value Pr(>F) ## TREAT 2 0.66 0.328 1.36 0.26 ## Residuals 69 16.59 0.240
-
Determine the regions of difference between each of the food
regimes pairwise using the Wilcox modification of the Johnson-Newman
procedure (with Games-Howell critical value approximation).
View full code
library(biology) constable.lm <- lm(SUTW ~ I(IV^(1/3)) * TREAT, constable) wilcox.JN(constable.lm, type = "H")
## df critical value lower upper ## High vs Initial 37 3.868 3.261 2.187 ## High vs Low 34 3.885 6.596 2.264 ## Initial vs Low 43 3.839 -1.547 2.939
- Present the results
of the Wilcox modification of the Johnson-Newman procedure in the
following table:>
Comparison df Critical value lower upper Initial vs low Initial vs High Low vs High - How about we finish with a summary graphic?
View full code
# fit the model and Wilcox modification of the Johnson-Newman library(biology) constable.lm <- lm(SUTW ~ I(IV^(1/3)) * TREAT, constable) WJN <- wilcox.JN(constable.lm, type = "H") # create base plot plot(SUTW ~ I(IV^(1/3)), constable, type = "n", ylim = c(0, 0.2), xlim = c(3, 50)^(1/3), axes = F, xlab = "", ylab = "") points(SUTW ~ I(IV^(1/3)), constable[constable$TREAT == "Initial", ], col = "black", pch = 22) lm1 <- lm(SUTW ~ I(IV^(1/3)), constable, subset = TREAT == "Initial") abline(lm1, col = "black", lty = 1) points(SUTW ~ I(IV^(1/3)), constable[constable$TREAT == "Low", ], col = "black", pch = 17) lm2 <- lm(SUTW ~ I(IV^(1/3)), constable, subset = TREAT == "Low") abline(lm2, col = "black", lty = 4) text(SUTW ~ I(IV^(1/3)), "\\#H0844", data = constable[constable$TREAT == "High", ], vfont = c("serif", "plain")) lm3 <- lm(SUTW ~ I(IV^(1/3)), constable, subset = TREAT == "High") abline(lm3, col = "black", lty = 2) axis(1, lab = c(10, 20, 30, 40, 50), at = c(10, 20, 30, 40, 50)^(1/3)) axis(2, las = 1) mtext("Initial body volume (ml)", 1, line = 3) mtext("Suture width (mm)", 2, line = 3) Mpar <- par(family = "HersheySans", font = 2) library(biology) # the legend.vfont function facilitates Hershey fonts legend.vfont("topleft", c("\\#H0841 Initial", "\\#H0844 High", "\\#H0852 Low"), bty = "n", lty = c(1, 2, 3), merge = F, title = "Food regime", vfont = c("serif", "plain")) par(Mpar) box(bty = "l") mn <- min(constable$IV^(1/3)) mx <- max(constable$IV^(1/3)) # since lower<upper (lines cross within the range - two regions # of significance (although one is # outside data range)) region capped to the data range arrows(WJN[3, 4], 0, mx, 0, ang = 90, length = 0.05, code = 3) text(mean(c(WJN[3, 4], mx)), 0.003, rownames(WJN)[3]) # since lower>upper (lines cross outside data range region capped to the data range if necessary arrows(min(WJN[2, 3], mx), 0.01, max(WJN[2, 4], mn), 0.01, ang = 90, length = 0.05, code = 3) text(mean(c(min(WJN[2, 3], mx), max(WJN[2, 4], mn))), 0.013, rownames(WJN)[2]) # since lower>upper (lines cross outside data range region capped to the data range if necessary arrows(min(WJN[1, 3], mx), 0.02, max(WJN[1, 4], mn), 0.02, ang = 90, length = 0.05, code = 3) text(mean(c(min(WJN[1, 3], mx), max(WJN[1, 4], mn))), 0.023, rownames(WJN)[1])
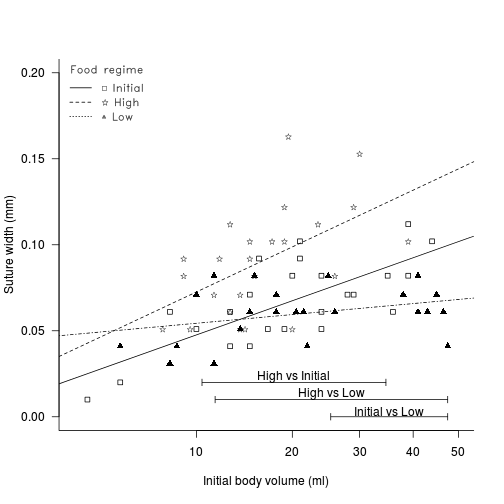
There is clear evidence that the relationships between suture width and initial volume differ between the three food regimes (slopes are not parallel and a significant interaction between food treatment and initial volume). Regular Ancova is not appropriate.
