Worksheet 7 - Exploratory data analysis
23 April 2011
Population parameters
The little spotted kiwi (Apteryx owenii) is a very rare flightless bird that is extinct on mainland New Zealand and survives as 1000 individuals on Kapiti Island. In order to monitor the population, researches in the recovery team systematically captured all of the individuals in the population over a two week period. Each individual was weighed, banded, assessed and released. The file *.csv lists the weights of each individual male little spotted kiwi in the population.
Download Kiwi data set| Format of kiwi.csv data file | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||
-
Open the kiwi data file. HINT.
Reveal code
> kiwi <- read.table("../downloads/data/kiwi.csv", header = T, sep = ",") > head(kiwi)
band malewt 1 64955 1.750 2 65318 2.551 3 64612 1.769 4 65393 2.327 5 65092 2.127 6 65406 2.174
-
Generate a frequency histogram
of male kiwi weights. HINT.
This distribution represents the population (all possible observations) of male kiwi
weights. Note that this is the statistical population and not a biological population
- obviously a biological population entirely lacking in females would not last long!
Show code
> hist(kiwi$malewt)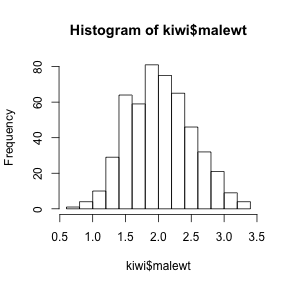
- Describe the shape of the distribution?
- What is the mean (a location measure) and standard deviation
(a measure of spread) of the population?
- Mean HINT
- SD HINT
Show code> mean(kiwi$malewt)[1] 2.026
> sd(kiwi$malewt)[1] 0.4836
- Mean HINT
- Assuming that the population is normally distributed, what is the
probability of recapturing a male little spotted kiwi that weighs greater than 2.9 kg?
HINT
Show code
> pnorm(2.9, mean = 2.025882, sd = 0.4836265, lower.tail = F)[1] 0.03535
- For data sets with large numbers of observations, the distribution of
observations can be examined via a histogram - as demonstrated above.
However, histograms are only meaningful for summarizing large data sets.
For smaller data sets other exploratory tools (such as
boxplots)
are necessary.
To appreciate the relationship between boxplots and the underlying distribution of data,
construct a boxplot
of male kiwi weights. HINT
Show code
> boxplot(kiwi$malewt)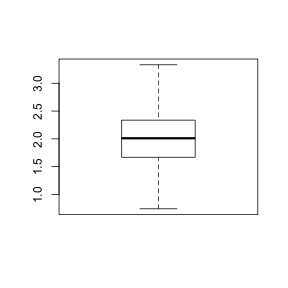
Since we have the weights of all male kiwi in the population, is possible to calculate population parameters (such as population mean and standard deviation) directly!
Assuming, the population is normally distributed, it is possible to calculate the probability that a randomly recaptured male kiwi will weigh greater than a particular value, less than a particular value, or weigh between a range of weights. This probability is just the area under a particular region of a normal distribution and can be calculated using the normal probabilities.
Samples as estimates of populations
Here is a modified example from Quinn and Keough (2002). Lovett et al. (2000) studied the chemistry of forested watersheds in the Catskill Mountains in New York State. They had 38 sites and recorded the concentrations of ten chemical variables, averaged over three years. We will look at two of these variables, dissolved organic carbon (DOC) and hydrogen ions (H).
Download Lovett data set| Format of lovett.csv data files | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||||||||
Open the lovett data file.
> lovett <- read.table("../downloads/data/lovett.csv", header = T, sep = ",", strip.white = T) > head(lovett)
STREAM DOC H 1 Santa Cruz 180.1 0.48 2 Colgate 98.8 0.24 3 Halsey 100.7 0.47 4 Batavia Hill 84.5 0.23 5 Windham Ridg 82.4 0.37 6 Silver Sprin 86.6 0.17
- What is the purpose of sampling?
- Construct a boxplot
of dissolved organic carbon (DOC) from the sample observations. HINT
Show code
> boxplot(lovett$DOC)
- How would you describe the
boxplot?
- Are there any outliers? (Y or N)
-
Calculate the sample mean
HINT
- Calculate the sample standard deviation
HINT
- Calculate the standard error of the mean HINT
Show code
> sd(lovett$DOC)/sqrt(length(lovett$DOC))
[1] 4.276
> # OR > library(gmodels) > ci(lovett$DOC)[4]
Std. Error 4.276 - Calculate the 95% confidence interval of the mean
HINT +/-Show code
> mean(lovett$DOC)[1] 71.66
> sd(lovett$DOC)[1] 26.36
> sd(lovett$DOC)/sqrt(length(lovett$DOC))
[1] 4.276
> qnorm(0.975, 0, 1) * (sd(lovett$DOC)/sqrt(length(lovett$DOC)))
[1] 8.38
> # OR > library(gmodels) > qnorm(0.975, 0, 1) * ci(lovett$DOC)[4]
Std. Error 8.38 - Construct a boxplot of hydrogen concentration (H) from the sample observations HINT
- How would you describe the boxplot?
- Many statistical analyses assume that the population from which the
sample was collected is normally distributed. However, biological data is not always
normally distributed. To normalize the data, try
transforming
to logs.
HINT
Show code
> boxplot(lovett$H)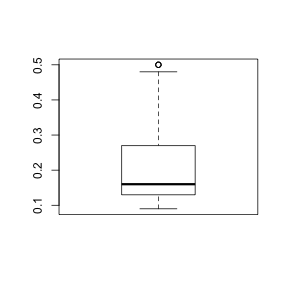
> boxplot(log10(lovett$H))
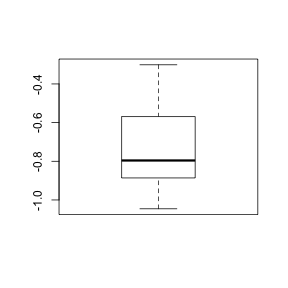
- Does the transformation
successfully normalize
these data? (Y or N)
- Which measures of location and spread are most robust to inclusion and exclusion of a single unusual observation?
Before continuing, make sure you are clear on what the observations, variables and populations are.
Provided the data were collected without bias (ideally random) and with adequate replication, the sample should reflect the entire population. Therefore sample statistics should be good estimates of the population parameters.
The mean of a sample is considered to be a location characteristic of the sample. Along with the mean, it is often desirable to characterize the spread of data in a sample - that is to determine how variable the sample is.
For most purposes, the sample itself is of little interest - it is purely used to estimate the population. Therefore it is necessary to be able to estimate how well the sample mean estimates the true population mean. The Standard error (SE) of the mean is a measure of the precision of the mean.
Following on from the idea of precision of the mean, is the concept of confidence intervals , by which an interval is calculated that we are 95% confident will contain the true population mean.
Earlier we identified the presence of an outlier, to investigate the impact of this outlier on a range of summary statistics, calculate the following measures of location (mean and median) and spread (standard deviation and interquartile range) for DOC, with and without the outlying observation and complete the table below.
| Summary Statistic | DOC | Modified DOC |
|---|---|---|
| Mean | HINT |
HINT |
| Median | HINT |
HINT |
| Variance | HINT |
HINT |
| Standard deviation | HINT |
HINT |
| Inter-quartile range | HINT |
HINT |
> mean(lovett$DOC)
[1] 71.66
> mean(lovett$DOC[lovett$DOC < 170])
[1] 68.73
> median(lovett$DOC)
[1] 66.7
> median(lovett$DOC[lovett$DOC < 170])
[1] 66.6
> var(lovett$DOC)
[1] 694.7
> var(lovett$DOC[lovett$DOC < 170])
[1] 378.5
> sd(lovett$DOC)
[1] 26.36
> sd(lovett$DOC[lovett$DOC < 170])
[1] 19.46
> diff(quantile(lovett$DOC, c(0.25, 0.75)))
75% 32.38
> diff(quantile(lovett$DOC[lovett$DOC < 170], c(0.25, 0.75)))
75% 33.2
Exploratory data analysis
Sánchez-Piñero & Polis (2000) studied the effects of seabirds on tenebrionid beetles on islands in the Gulf of California. These beetles are the dominant consumers on these islands and it was envisaged that seabirds leaving guano and carrion would increase beetle productivity. They had a sample of 25 islands and recorded the beetle density, the type of bird colony (roosting, breeding, no birds), % cover of guano and % plant cover of annuals and perennials.
Download Sanchez data set| Format of sanchez.csv data files | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||||||||
Open the sanchez data file.
> sanchez <- read.table("../downloads/data/sanchez.csv", header = T, sep = ",") > head(sanchez)
COLTYPE BEETLE96 GUANO PLANT96 1 R 69.00 12.1 5.60 2 N 2.80 0.0 5.86 3 N 14.33 0.0 30.30 4 B 141.00 60.0 7.80 5 N 1.00 0.0 21.60 6 N 35.20 5.5 3.10
- For percentage plant cover, Calculate the following summary statistics separately for each colony type and complete the table below.
- Which colony type has the greatest variance? (N, R or B)
- Construct a
boxplot
for total 1996 beetle abundance for each colony type separately. HINT
- Are there any outliers identified? (Y or N)
- Describe the shape of each distribution.
- Now transform the response variable to logs and redraw the boxplots HINT. Does this change (improve?) the shape of the distributions? (Y or N)
Show code> boxplot(PLANT96 ~ COLTYPE, data = sanchez)
> boxplot(log10(PLANT96) ~ COLTYPE, data = sanchez)
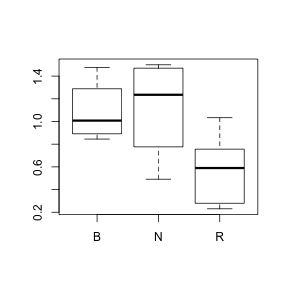
- Are there any outliers identified? (Y or N)
- Construct a
scatterplot
for beetle abundance
against
total 1996 plant cover (HINT).
- Is there any evidence of non-linearity? (Y or N)
- Note, that the boxplots also enable us to explore the normality of both variables (populations). Is there any evidence of non-normality? (Y or N)
Show code> library(car) > scatterplot(BEETLE96 ~ PLANT96, data = sanchez)
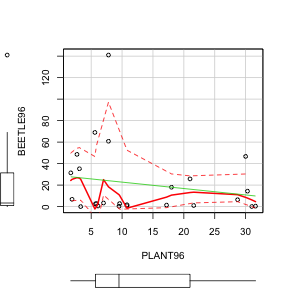
- Is there any evidence of non-linearity? (Y or N)
- Construct a
scatterplot matrix or SPLOM
for % of guano, % of plant cover and beetle abundance HINT. Are there any obvious relationships?
Show code> library(car) > scatterplot.matrix(~BEETLE96 + PLANT96 + GUANO, data = sanchez, diagonal = "boxplot")
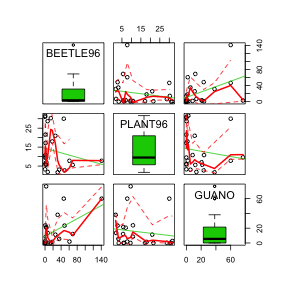
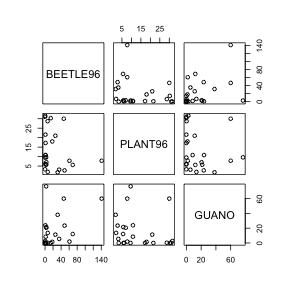
> # OR > pairs(~BEETLE96 + PLANT96 + GUANO, data = sanchez)
- Construct an examine
boxplots
of beetle abundance for each of the three colony types. HINT
- Firstly, is there any evidence of non-normality? (Y or N)
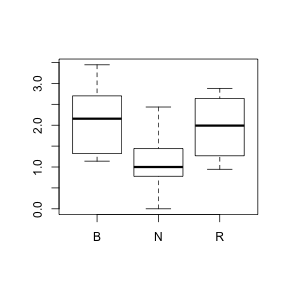
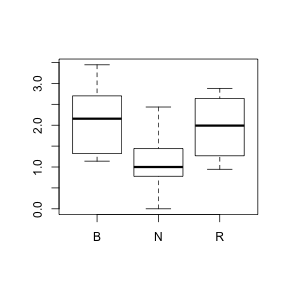
- Try square-root transforming (preferred over log transformation when applying to count data, since log(0) is not legal) the beetle variable (function is sqrt) and using this transformed variable to reconstruct the boxplots. Note that it may be necessary to perform a forth-root transformation (which performing the square-root transformation twice) in order to normalize this highly skewed data. This can be done using the expression to compute as sqrt(sqrt(BEETLE96)) HINT or HINT. If this successfully normalizes the data, focus on whether there is any evidence that the populations are equally varied. Was a forth-root transformation successfull? (Y or N)
- Try calculating the variance or standard deviation
of beetle abundance for each colony type separately (remember to use the transformed data, as the raw data was obviously non-normal and non-normality often results in unequal variances). Do these values provide any evidence for unequally varied populations? (Y or N)
Show code> boxplot(BEETLE96 ~ COLTYPE, data = sanchez)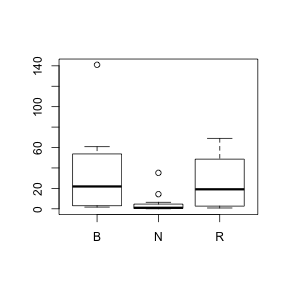
> boxplot(sqrt(sqrt(BEETLE96)) ~ COLTYPE, data = sanchez)
> # OR > boxplot(BEETLE96^0.25 ~ COLTYPE, data = sanchez)
> > tapply(sqrt(sqrt(sanchez$BEETLE96)), sanchez$COLTYPE, mean)
B N R 2.119 1.117 1.953
> tapply(sqrt(sqrt(sanchez$BEETLE96)), sanchez$COLTYPE, var)
B N R 0.6729 0.4601 0.6206
- Firstly, is there any evidence of non-normality? (Y or N)
| Summary Statistic | No colonies | Roosting colony | Breeding colony |
|---|---|---|---|
| Mean HINT | |||
| Variance HINT | |||
| Standard deviation HINT |
> tapply(sanchez$PLANT96, sanchez$COLTYPE, mean)
B N R 14.000 17.115 4.733
> tapply(sanchez$PLANT96, sanchez$COLTYPE, var)
B N R 68.07 142.41 11.97
> tapply(sanchez$PLANT96, sanchez$COLTYPE, sd)
B N R 8.25 11.93 3.46
Normality
Before proceeding, make sure you are familiar with the significance of normally distributed sample data and thus why it is necessary to examine the distribution of sample data as part of routine exploratory data analysis (EDA) prior to any formal data analysis.
Linearity
Often it is necessary to examine the nature of the relationship or association between as part of routine exploratory data analysis (EDA) prior to any formal data analysis. The nature of relationships/associations between continuous data is explored using scatterplots.
Sánchez-Piñero & Polis (2000) measured a number of continuous variables (% cover of guano, % cover or plants and abundance of beetles. Therefore, they might be interested in exploring the relationships between each of these variables. That is, the relationship between guano and plants, guano and beetles, and beetles and plants. While it is possible to create separate scatterplots for each pair (in this case three separate scatterplots), a scatterplot matrix is usually more informative and efficient.
Homogeneity of variance
Many statistical hypothesis tests assume that populations are equally varied. For hypothesis tests that compare populations, it is important that one of the populations is not substantially more or less variable than the other population(s). Thus, such tests assume homogeneity of variance.
