Tutorial 7.3a - Multiple linear regression
15 Jun 2019
Preliminaries
The following packages will be used in this tutorial:
library(car) library(effects) library(emmeans) library(ggfortify) library(ggeffects) library(GGally) library(MuMIn) library(scales) library(broom) library(tidyverse)
Multiple and complex regression analyses can be useful for situations in which patterns in a response variable can not be adequately described by a single straight line resulting from a single predictor and/or a simple linear equation.
Overview
Multiple regression is an extension of simple linear regression whereby a response variable is modeled against a linear combination of two or more simultaneously measured continuous predictor variables. There are two main purposes of multiple linear regression:
- To develop a better predictive model (equation) than is possible from models based on single independent variables.
- To investigate the relative individual effects of each of the multiple independent variables above and beyond (standardized across) the effects of the other variables.
Although the relationship between response variable and the additive effect of all the predictor variables is represented overall by a single multidimensional plane (surface), the individual effects of each of the predictor variables on the response variable (standardized across the other variables) can be depicted by single partial regression lines. The slope of any single partial regression line (partial regression slope) thereby represents the rate of change or effect of that specific predictor variable (holding all the other predictor variables constant to their respective mean values) on the response variable. In essence, it is the effect of one predictor variable at one specific level (the means) of all the other predictor variables (i.e. when each of the other predictors are set to their averages).
Multiple regression models can be constructed additively (containing only the predictor variables themselves) or in a multiplicative design (which incorporate interactions between predictor variables in addition to the predictor variables themselves). Multiplicative models are used primarily for testing inferences about the effects of various predictor variables and their interactions on the response variable in much the same way as factorial ANOVA. Additive models by contrast are used for generating predictive models and estimating the relative importance of individual predictor variables more so than hypothesis testing.
Linear models
Additive model
$$y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+...+\beta_jx_{ij}+\epsilon_i$$ where $\beta_0$ is the population y-intercept (value of $y$ when all partial slopes equal zero), $\beta_1$, $\beta_2$, etc are the partial population slopes of $Y$ on $X_1$, $X_2$, etc respectively holding the other $X$ constant. $\epsilon_i$ is the random unexplained error or residual component.
The additive model assumes that the effect of one predictor variable (partial slope) is independent of the levels of the other predictor variables.
Multiplicative model
$$y_i=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i1}x_{i2}+...+\epsilon_i$$ where $\beta_3x_{i1}x_{i2}$ is the interactive effect of $X_1$ and $X_2$ on $Y$ and it examines the degree to which the effect of one of the predictor variables depends on the levels of the other predictor variable(s).
Since for gaussian (normal distribution) regression, the range of values for any given predictor (such as temperature) is generally substantially away from zero, the value of the y-intercept (value of y when x is equal to zero) is usually of little interest. It commonly represents a value of y for a value of x that may well be either impossible or else highly unlikely. However, if the predictor variable(s) are centered (the scale is shifted such that the mean of the predictor is zero), then the y-intercept represents the value of y in the middle of the range of x - and is thus more meaningful.
Null hypotheses
There are separate null hypotheses associated with each of the estimated parameters (including the intercept). $$H_0: \beta_0=0 \quad\mathsf{(the~population~y-intercept~equals~zero)}$$ This test is rarely of much interest as it only tests the likelihood that the background level of the response variable is equal to zero (rarely a ecologically meaningful comparison). $$H_0: \beta_1=0 \quad\mathsf{(the~partial~population~slope~of~X_1~on~Y~equals~zero)}$$ $$H_0: \beta_2=0 \quad\mathsf{(the~partial~population~slope~of~X_2~on~Y~equals~zero)}$$ Technically, these tests examine respectively whether or not there is sufficient data to conclude there is a relationship between the dependent and one of the independent variables (holding the other independent variables constant) in the population. Less formally, they are used to conclude whether or not there is evidence of the respective relationships.
For multiplicative models
$$H_0: \beta_3=0 \quad\mathsf{(the~partial~population~slope~of~the~interactive~effect~of~X_1~and~X_2~equals~zero)}$$ The estimated interaction parameter ($\beta_3$ in this case), represents the degree to which the partial slope of one of the covariates deviates throughtout the range of the other covariate(s). The assocatiate hypotheses tests thus examine whether or not the effect of one covariate (dependent variable) on the independent variable (holding others constant) is dependent on other independent variables.
Scenario and Data
Lets say we had set up a natural experiment in which we measured a response ($y$) from each of 20 sampling units ($n=20$) across a landscape. At the same time, we also measured two other continuous covariates ($x1$ and $x2$) from each of the sampling units. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
set.seed(3) n = 100 intercept = 5 temp = runif(n) nitro = runif(n) + 0.8 * temp int.eff = 2 temp.eff <- 0.85 nitro.eff <- 0.5 res = rnorm(n, 0, 1) coef <- c(int.eff, temp.eff, nitro.eff, int.eff) mm <- model.matrix(~temp * nitro) y <- t(coef %*% t(mm)) + res data <- data.frame(y, x1 = temp, x2 = nitro, cx1 = scale(temp, scale = F), cx2 = scale(nitro, scale = F))
With these sort of data, we are primarily interested in investigating whether there is a relationship between the continuous response variable and the components linear predictor (continuous predictors). We could model the relationship via either:
- an additive model in which the effects of each predictor contribute in an additive way to the response - we do not allow for an interaction as we consider an interaction either not of great importance or likely to be absent.
- and multiplicative model in which the effects of each predictor and their interaction contribute to the response - we allow for the impact of one predictor to vary across the range of the other predictor.
Centering data
When a linear model contains a covariate (continuous predictor variable) in addition to another predictor (continuous or categorical), it is nearly always advisable that the continuous predictor variables be centered prior to the analysis. Centering is a process by which the mean of a variable is subtracted from each of the values such that the scale of the variable is shifted so as to be centered around 0. Hence the mean of the new centered variable will be 0, yet it will retain the same variance.
| Raw data | Centered X |
|---|---|
 |
 |
There are multiple reasons for centering data:
- Firstly, it provides some biological meaning to the y-intercept. Recall that the y-intercept is the value of Y when X is equal to zero. If X is centered, then the y-intercept represents the value of Y at the mid-point of the X range. The y-intercept of an un-centered X typically represents a un-real value of Y (as an X of 0 is often beyond the reasonable range of values).
- Secondly, in multiplicative models (in which predictors and their interactions are included), main effects and interaction terms built from centered predictors will not be correlated to one another (see below)
- Thirdly, for more complex models, centering the covariates can increase the likelihood that the modelling engine will converge (arrive at a numerically stable and reliable outcome).
In R, centering is easily achieved with the scale function. Alternatively, each observation can be subtracted from the mean of the variable.
data <- within(data, { cx1 <- as.numeric(scale(x1, scale = FALSE)) cx2 <- as.numeric(scale(x2, scale = FALSE)) }) head(data)
y x1 x2 cx1
1 3.513305 0.1680415 0.9007709 -0.31604197
2 5.090382 0.8075164 1.3281453 0.32343291
3 4.036943 0.3849424 0.5170847 -0.09914114
4 4.006436 0.3277343 0.9741312 -0.15634918
5 5.381677 0.6021007 1.0869787 0.11801718
6 4.530071 0.6043941 0.8240744 0.12031056
cx2
1 0.02986272
2 0.45723717
3 -0.35382350
4 0.10322304
5 0.21607055
6 -0.04683372
Exploratory data analysis and initial assumption checking
- All of the observations are independent - this must be addressed at the design and collection stages or specifically accounted for in the variance-covariance structure.
- The response variable (and thus the residuals) should be normally distributed. A boxplot of the entire variable is usually useful for diagnosing major issues with normality.
- The response variable should be equally varied (variance should not be related to mean as these are supposed to be estimated separately). Scatterplots with linear smoothers can be useful for exploring the spread of observations around the trendline. The spread of observations around the trendline should not increase (or decrease) along its length.
- The predictor variables should be uniformly or normally distributed. Again, boxplots can be useful.
- The relationships between the linear predictors (right hand side of the regression formula) and the response variable should be linear. Scatterplots with smoothers can be useful for identifying possible non-linearity.
- (Multi)collinearity - see below
- The number of predictor variables must be less than the number of observations otherwise the linear model will be over-parameterized (more parameters to estimate than there are independent data from which estimations are calculated).
(Multi)collinearity - a predictor variable must not be correlated to the combination of other predictor variables (known collectively as the linear predictor). Multicollinearity has major detrimental effects on model fitting:
- instability of the estimated partial regression slopes (small changes in the data or variable inclusion can cause dramatic changes in parameter estimates)
- inflated standard errors and confidence intervals of model parameters, thereby increasing the type II error rate (reducing power) of parameter hypothesis tests
- investigate pairwise correlations between all the predictor variables either by a correlation matrix or a scatterplot matrix
- calculate tolerance ($1-r^2$) of the relationship between a predictor variable and all the other predictor variables) for each of the predictor variables. Tolerance is a measure of the degree of collinearity and values less $<0.2$ should be considered and values $<0.1$ given series attention. Variance inflation factor (VIF) are the inverse of tolerance and thus values greater than 5, or worse, 10 indicate collinearity. Many practitioners advocate a VIF cut off of 3 which equates to an $R^2$ of approximately 0.667.
- PCA (principle components analysis) eigenvalues (from a correlation matrix for all the predictor variables) close to zero indicate collinearity and component loadings may be useful in determining which predictor variables cause collinearity.
- remove the highly correlated predictor variable(s), starting with the least most biologically interesting variable(s)
- PCA (principle components analysis) or similar multivariate regression - regress the response variable against the principal components resulting from a correlation matrix for all the predictor variables. Each of these principal components by definition are completely independent, but the resulting parameter estimates must be back-calculated in order to have any biological meaning.
- apply a regression tree - regression trees recursively partitioning (subsetting) the data in accordance to individual variables that explain the greatest remaining variance. Since at each iteration, each predictor variable is effectively evaluated in isololation, (multi)collinearity is not an issue.
Normality, homogeneity of variance and linearity - scatterplot matrix
# define a boxplot panel function panel.bxp <- function(x, ...) { usr <- par("usr") on.exit(par(usr)) par(usr = c(usr[1:2], 0, 2)) boxplot(x, add = TRUE, horizontal = T) } pairs(~y + cx1 + cx2, data = data, lower.panel = panel.smooth, diag.panel = panel.bxp, upper.panel = NULL, gap = 0)
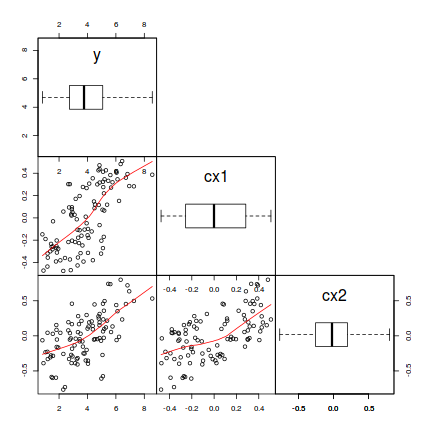
# OR the ggplot way library(GGally) ggpairs(data[, c("y", "cx1", "cx2")], lower = list(continuous = "smooth"), diag = list(continuous = "density"), axisLabels = "show")
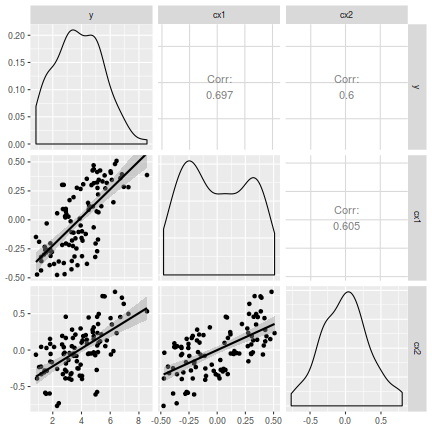
- There is no evidence of non-normality in either the response or the covariates (whilst the distribution of cx2 is a little strange, it is nonetheless symmetrical).
- An increase in cx1 appears to be associated with a positive increase in $y$ and a linear fit would seem sensible (the smoother maintains a constant direction)
- There is a fairly even spread of values around the smoother (suggesting homogeneity of variance holds).
- An increase in cx2 does not appear to be associated with a consistent change in $y$, yet a linear fit is no less sensible than any other.
- cx1 and cx2 do not appear to be strongly correlated to one another
(Multi)collinearity
In R, collinearity can be explored either by exploring the correlations between individual pairs of predictors (as in the scatterplot matrix above) or via the VIF() function (car package). Note, when a model includes multiple predictors and their interactions, the individual predictors will be correlated to their interactions.
library(car) # additive model - scaled predictors vif(lm(y ~ cx1 + cx2, data))
cx1 cx2 1.576619 1.576619
# multiplicative model - raw predictors vif(lm(y ~ x1 * x2, data))
x1 x2 x1:x2 9.773606 4.962009 18.953891
# multiplicative model - scaled predictors vif(lm(y ~ cx1 * cx2, data))
cx1 cx2 cx1:cx2 1.589502 1.580201 1.024682
- For the additive model, the variance-inflation factors are less than 5, suggesting that collinearity is not an issue.
- For the multiplicative model (with raw predictors), the variance-inflation factors are far greater than 5, suggesting that collinearity is likely to be a huge issue with the raw data fitted with a multiplicative model.
- For the multiplicative model (with scaled predictors), the variance-inflation factors are less than 5 (or even the more conservative value of 3), suggesting that collinearity is not an issue.
Model fitting or statistical analysis
In R, multiple linear regression models are fit using the lm() function. The most important (=commonly used) parameters/arguments for simple regression are:
- formula: the linear model relating the response variable to the linear predictor
- data: the data frame containing the data
- additive model
data.add.lm <- lm(y ~ cx1 + cx2, data)
- multiplicative model
data.mult.lm <- lm(y ~ cx1 + cx2 + cx1:cx2, data) # OR data.mult.lm <- lm(y ~ cx1 * cx2, data)
| Extractor | Description |
|---|---|
| residuals() | Extracts the residuals from the model |
| fitted() | Extracts the predicted (expected) response values (on the link scale) at the observed levels of the linear predictor |
| predict() | Extracts the predicted (expected) response values (on either the link, response or terms (linear predictor) scale) |
| coef() | Extracts the model coefficients |
| summary() | Summarizes the important output and characteristics of the model |
| anova() | Computes an analysis of variance (variance partitioning) from the model |
| plot() | Generates a series of diagnostic plots from the model |
| influence.measures() | Calculates a range of regression diagnostics including leverage and Cook's D |
| allEffects() | Estimates highest level interaction effects from a fitted model. From the effects package. Useful in combination with plot |
| AIC() | Extracts the Akaike's Information Criterion |
Model evaluation
Prior to exploring the model parameters, it is prudent to confirm that the model did indeed fit the assumptions and was an appropriate fit to the data.
As part of linear model fitting, a suite of diagnostic measures can be calculated each of which provide an indication of the appropriateness of the model for the data and the indication of each points influence (and outlyingness) of each point on resulting the model.
Leverage
Leverage is a measure of how much of an outlier each point is in x-space (on x-axis) and thus only applies to the predictor variable. Values greater than $2\times p/n$ (where p=number of model parameters ($p = 2$ for simple linear regression), and $n$ is the number of observations) should be investigated as potential outliers.Residuals
As the residuals are the differences between the observed and predicted values along a vertical plane, they provide a measure of how much of an outlier each point is in y-space (on y-axis). Outliers are identified by relatively large residual values. Residuals can also standardized and studentized, the latter of which can be compared across different models and follow a t distribution enabling the probability of obtaining a given residual can be determined. The patterns of residuals against predicted y values (residual plot) are also useful diagnostic tools for investigating linearity and homogeneity of variance assumptions.Cook's D
Cook's D statistic is a measure of the influence of each point on the fitted model (estimated slope) and incorporates both leverage and residuals. Values > 1 (or even approaching 1) correspond to highly influential observations.Lets explore the diagnostics - particularly the residuals
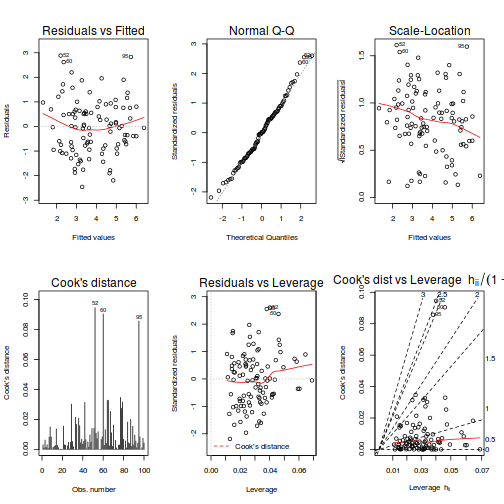
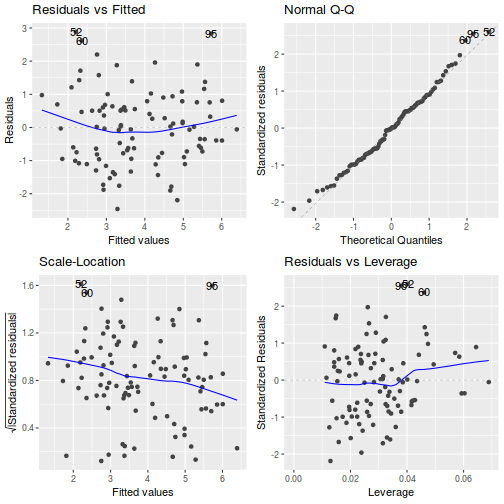
# Additive model par(mfrow = c(2, 3)) plot(data.add.lm, ask = F, which = 1:6)
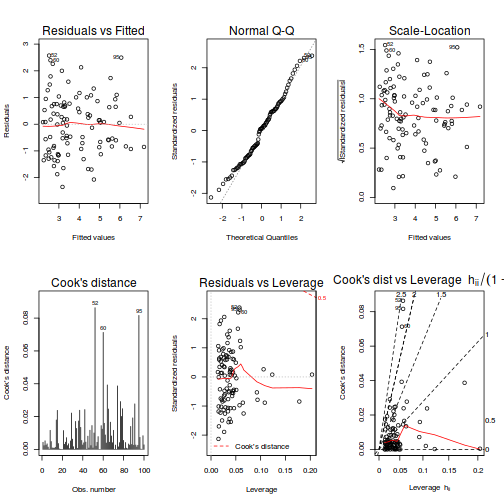
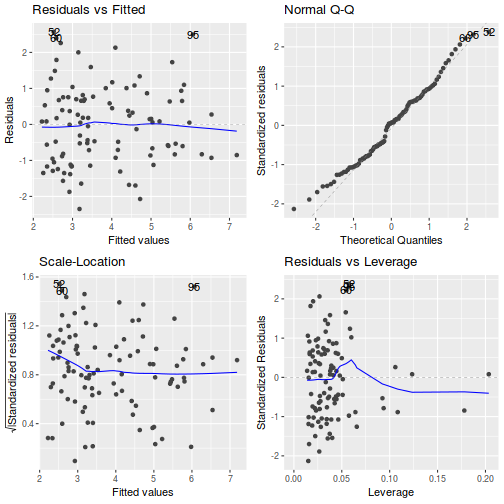
# Multiplicative model par(mfrow = c(2, 3)) plot(data.mult.lm, ask = F, which = 1:6)
## Additive model autoplot(data.add.lm)
## Multiplicative model autoplot(data.mult.lm)
# Additive model influence.measures(data.add.lm)
Influence measures of
lm(formula = y ~ cx1 + cx2, data = data) :
dfb.1_ dfb.cx1 dfb.cx2 dffit cov.r cook.d
1 0.05496 -0.080304 5.25e-02 0.09744 1.055 3.19e-03
2 -0.03139 -0.011902 -2.72e-02 -0.05475 1.061 1.01e-03
3 0.09076 0.033825 -9.75e-02 0.13691 1.029 6.26e-03
4 0.04603 -0.042590 3.72e-02 0.06433 1.045 1.39e-03
5 0.08067 0.002073 4.06e-02 0.09629 1.026 3.10e-03
6 0.03639 0.023196 -1.81e-02 0.04346 1.042 6.35e-04
7 0.06507 0.005618 -1.17e-01 0.15734 1.082 8.30e-03
8 -0.17037 0.051253 6.45e-02 -0.21453 0.960 1.51e-02
9 -0.08625 -0.100633 1.29e-01 -0.15784 1.044 8.33e-03
10 0.02363 0.018197 -1.40e-02 0.03007 1.047 3.04e-04
11 -0.05598 -0.024339 3.30e-02 -0.06522 1.036 1.43e-03
12 -0.04275 -0.041954 6.52e-02 -0.07806 1.061 2.05e-03
13 -0.05618 -0.050095 6.99e-02 -0.09019 1.049 2.73e-03
14 0.12664 0.119852 -1.55e-01 0.20305 1.009 1.37e-02
15 -0.03702 -0.000204 -6.53e-02 -0.09015 1.092 2.73e-03
16 -0.03224 -0.012583 -3.07e-02 -0.05926 1.064 1.18e-03
17 0.00152 -0.002631 1.73e-03 0.00304 1.075 3.12e-06
18 0.01556 0.002327 1.19e-02 0.02300 1.054 1.78e-04
19 -0.00605 -0.010142 5.22e-03 -0.01186 1.073 4.74e-05
20 -0.00308 0.001476 4.67e-04 -0.00382 1.048 4.91e-06
21 -0.13925 0.166109 -1.10e-01 -0.21708 0.997 1.56e-02
22 0.04341 -0.086055 4.82e-02 0.09650 1.079 3.13e-03
23 0.04617 -0.077863 5.30e-02 0.09082 1.066 2.77e-03
24 -0.00279 0.000998 3.39e-03 -0.00582 1.079 1.14e-05
25 0.06122 -0.055452 2.17e-02 0.08392 1.039 2.36e-03
26 -0.08076 -0.073832 7.47e-03 -0.11896 1.034 4.74e-03
27 0.02497 -0.001355 1.56e-02 0.03113 1.046 3.26e-04
28 -0.06588 -0.081909 5.70e-03 -0.11865 1.052 4.72e-03
29 -0.16460 0.116860 -2.51e-01 -0.30364 0.985 3.02e-02
30 0.08473 0.090886 -4.39e-02 0.12503 1.032 5.23e-03
31 0.05713 0.006562 -3.86e-02 0.07206 1.038 1.74e-03
32 0.00614 -0.001891 -1.54e-05 0.00658 1.043 1.46e-05
33 0.15662 -0.074310 -1.04e-01 0.25526 0.984 2.14e-02
34 -0.15974 -0.082679 1.59e-01 -0.22635 0.975 1.68e-02
35 0.00279 -0.003831 3.43e-03 0.00494 1.065 8.22e-06
36 -0.22468 0.113773 -3.46e-02 -0.25548 0.898 2.09e-02
37 0.10028 0.193093 -1.31e-01 0.21835 1.051 1.59e-02
38 -0.05517 -0.007116 8.37e-02 -0.11418 1.068 4.38e-03
39 -0.12895 -0.004978 -4.85e-02 -0.14432 0.993 6.90e-03
40 -0.07301 0.061080 -7.71e-03 -0.10202 1.035 3.49e-03
41 -0.10400 0.055209 6.10e-03 -0.12776 1.013 5.44e-03
42 -0.20164 -0.232856 1.03e-01 -0.31159 0.936 3.14e-02
43 -0.08698 0.108746 -5.48e-02 -0.13993 1.035 6.55e-03
44 -0.01900 0.012188 -2.78e-02 -0.03414 1.065 3.92e-04
45 0.07188 -0.071790 9.72e-02 0.12198 1.046 4.98e-03
46 0.04558 -0.002854 -4.09e-02 0.07034 1.050 1.66e-03
47 -0.09203 0.129092 -2.79e-02 -0.17061 1.041 9.72e-03
48 -0.05885 0.104474 -6.92e-02 -0.12015 1.065 4.85e-03
49 0.17006 -0.116546 5.90e-02 0.20666 0.959 1.40e-02
50 0.01065 0.015622 -1.03e-02 0.01893 1.065 1.21e-04
51 -0.12313 0.162253 -1.23e-01 -0.20613 1.014 1.41e-02
52 0.27403 0.033407 -3.99e-01 0.54950 0.865 9.46e-02
53 0.07540 0.006550 1.26e-01 0.18005 1.076 1.09e-02
54 0.06972 0.119259 -3.31e-02 0.14656 1.064 7.20e-03
55 0.10615 0.058275 8.04e-02 0.18903 1.030 1.19e-02
56 0.00181 0.002906 -1.24e-03 0.00349 1.071 4.09e-06
57 -0.00701 -0.004934 8.57e-03 -0.01108 1.058 4.13e-05
58 -0.06882 -0.013504 1.05e-01 -0.14029 1.061 6.60e-03
59 -0.09808 0.079713 2.97e-02 -0.15982 1.029 8.52e-03
60 0.24873 0.122348 -4.37e-01 0.53380 0.904 9.04e-02
61 -0.03663 0.008481 -7.02e-02 -0.08999 1.094 2.72e-03
62 0.11057 -0.127593 -6.97e-03 0.19917 1.028 1.32e-02
63 0.07126 0.078309 -2.45e-02 0.10970 1.040 4.03e-03
64 0.14691 -0.276780 2.00e-01 0.31599 1.015 3.29e-02
65 0.17537 0.018974 1.98e-01 0.31631 0.973 3.27e-02
66 0.05501 -0.060135 5.39e-02 0.08441 1.047 2.39e-03
67 0.12775 -0.024794 2.09e-01 0.27662 1.031 2.54e-02
68 -0.12072 -0.101373 1.36e-01 -0.18347 1.010 1.12e-02
69 0.04999 -0.050322 5.51e-02 0.07739 1.049 2.01e-03
70 0.13042 -0.150583 1.30e-02 0.22203 1.009 1.63e-02
71 0.01165 0.007906 1.77e-03 0.01631 1.052 8.95e-05
72 -0.07039 -0.110563 9.28e-02 -0.13505 1.055 6.11e-03
73 0.02971 0.025083 1.61e-02 0.05526 1.066 1.03e-03
74 -0.00544 -0.001608 -9.46e-03 -0.01427 1.108 6.86e-05
75 -0.06183 -0.046836 6.85e-02 -0.09255 1.043 2.87e-03
76 0.09134 0.005707 1.82e-02 0.09546 1.017 3.04e-03
77 0.20275 -0.253784 1.19e-01 0.32763 0.937 3.47e-02
78 -0.15914 0.239984 -1.62e-01 -0.28872 0.989 2.74e-02
79 -0.17534 -0.255279 1.77e-01 -0.31101 0.972 3.16e-02
80 -0.09973 -0.049729 -4.09e-02 -0.14266 1.022 6.79e-03
81 0.00252 0.003611 -2.47e-03 0.00442 1.064 6.58e-06
82 -0.10007 -0.084251 6.06e-02 -0.13137 1.018 5.75e-03
83 0.03255 0.015136 -4.10e-02 0.05371 1.057 9.71e-04
84 0.09210 -0.031634 -1.50e-01 0.23377 1.076 1.83e-02
85 -0.05641 -0.097669 3.86e-02 -0.11567 1.067 4.49e-03
86 -0.06549 -0.081108 2.68e-02 -0.10793 1.047 3.91e-03
87 -0.12962 0.200250 -1.69e-01 -0.24599 1.018 2.00e-02
88 0.04607 0.039184 -6.25e-02 0.07769 1.055 2.03e-03
89 0.17760 0.124772 -8.14e-02 0.21718 0.952 1.54e-02
90 -0.05092 -0.075904 2.27e-02 -0.09594 1.061 3.09e-03
91 -0.08708 0.103630 1.88e-02 -0.16964 1.048 9.62e-03
92 -0.07103 0.099397 -9.32e-02 -0.12905 1.051 5.58e-03
93 0.04831 0.011828 -3.04e-02 0.05767 1.039 1.12e-03
94 0.06870 0.049419 2.80e-02 0.11151 1.044 4.17e-03
95 0.26778 0.130837 2.62e-01 0.52231 0.871 8.57e-02
96 -0.11687 0.045321 5.09e-02 -0.15934 1.008 8.43e-03
97 -0.00518 0.006167 -6.37e-03 -0.00871 1.062 2.56e-05
98 -0.03021 0.043080 -4.64e-02 -0.05849 1.069 1.15e-03
99 -0.09996 0.061999 3.60e-02 -0.14951 1.024 7.45e-03
100 -0.08128 -0.079058 5.71e-02 -0.11399 1.031 4.35e-03
hat inf
1 0.0314
2 0.0304
3 0.0228
4 0.0195
5 0.0142
6 0.0143
7 0.0585
8 0.0159
9 0.0335
10 0.0162
11 0.0136
12 0.0333
13 0.0258
14 0.0257
15 0.0593
16 0.0338
17 0.0401
18 0.0218
19 0.0385
20 0.0154
21 0.0243
22 0.0494
23 0.0387
24 0.0436
25 0.0188
26 0.0217
27 0.0155
28 0.0324
29 0.0340
30 0.0218
31 0.0159
32 0.0115
33 0.0266
34 0.0201
35 0.0314
36 0.0129 *
37 0.0474
38 0.0428
39 0.0125
40 0.0195
41 0.0151
42 0.0239
43 0.0259
44 0.0323
45 0.0288
46 0.0238
47 0.0344
48 0.0417
49 0.0148
50 0.0316
51 0.0280
52 0.0402 *
53 0.0570
54 0.0442
55 0.0317
56 0.0371
57 0.0250
58 0.0416
59 0.0266
60 0.0461 *
61 0.0603 *
62 0.0324
63 0.0237
64 0.0463
65 0.0325
66 0.0235
67 0.0469
68 0.0231
69 0.0240
70 0.0290
71 0.0196
72 0.0368
73 0.0346
74 0.0689 *
75 0.0224
76 0.0109
77 0.0261
78 0.0329
79 0.0315
80 0.0205
81 0.0307
82 0.0172
83 0.0272
84 0.0644
85 0.0420
86 0.0272
87 0.0360
88 0.0284
89 0.0150
90 0.0355
91 0.0379
92 0.0330
93 0.0142
94 0.0264
95 0.0380 *
96 0.0186
97 0.0283
98 0.0375
99 0.0224
100 0.0197
# Multiplicative model influence.measures(data.mult.lm)
Influence measures of
lm(formula = y ~ cx1 * cx2, data = data) :
dfb.1_ dfb.cx1 dfb.cx2 dfb.c1.2 dffit cov.r
1 0.08238 -0.098107 0.068949 -0.043295 0.13160 1.060
2 -0.02099 -0.015304 -0.041455 -0.039682 -0.09580 1.072
3 0.08806 0.036729 -0.102033 -0.013545 0.14495 1.028
4 0.08072 -0.054767 0.054168 -0.049401 0.10249 1.052
5 0.09928 0.005977 0.048161 -0.040225 0.11699 1.024
6 0.06625 0.037504 -0.024731 -0.039350 0.07504 1.051
7 -0.00437 -0.001207 -0.016173 0.021433 0.02954 1.189
8 -0.14862 0.051463 0.065216 0.004465 -0.21802 0.938
9 -0.09088 -0.083703 0.097259 0.063936 -0.13840 1.070
10 0.05179 0.034457 -0.022949 -0.031718 0.06128 1.059
11 -0.05121 -0.021037 0.023813 0.028282 -0.05723 1.054
12 -0.03466 -0.029972 0.043143 0.019135 -0.05614 1.080
13 -0.05081 -0.038795 0.048894 0.030940 -0.07207 1.070
14 0.19262 0.151795 -0.176840 -0.124490 0.26961 0.986
15 0.03190 0.018158 -0.155239 -0.207408 -0.30827 1.132
16 -0.01645 -0.016734 -0.051077 -0.058656 -0.11949 1.077
17 0.01942 -0.027085 0.019025 -0.010610 0.03426 1.090
18 0.01119 0.001977 0.010675 0.001184 0.02071 1.065
19 0.00618 0.009451 -0.004605 -0.002862 0.01117 1.087
20 -0.00081 0.000422 0.000132 0.000092 -0.00112 1.059
21 -0.15092 0.145425 -0.105088 0.079312 -0.21533 1.003
22 0.04892 -0.097523 0.056066 -0.012538 0.11178 1.087
23 0.07762 -0.102375 0.074749 -0.045014 0.13253 1.073
24 0.01882 0.030843 0.073270 -0.122852 -0.16894 1.136
25 0.06948 -0.060454 0.025498 -0.020781 0.09696 1.043
26 -0.07278 -0.073133 0.006802 0.010916 -0.11724 1.039
27 0.03662 -0.000595 0.022148 -0.014064 0.04519 1.056
28 -0.04658 -0.092807 0.008385 -0.035310 -0.14400 1.054
29 -0.16561 0.107730 -0.246245 0.057425 -0.30009 0.976
30 0.11573 0.111914 -0.048868 -0.058686 0.15855 1.027
31 0.06255 0.008755 -0.042252 -0.016150 0.08210 1.043
32 0.01841 -0.004413 0.000339 -0.008005 0.01965 1.056
33 0.04735 -0.077683 -0.098933 0.131464 0.26241 1.000
34 -0.16728 -0.085046 0.148517 0.072010 -0.22765 0.970
35 0.03448 -0.032122 0.032011 -0.024819 0.05093 1.085
36 -0.23868 0.101319 -0.038471 0.100549 -0.26840 0.872
37 0.18057 0.257770 -0.161105 -0.135266 0.30992 1.038
38 -0.00569 0.000290 0.144957 -0.133689 -0.23170 1.078
39 -0.13516 -0.010299 -0.048045 0.063148 -0.14841 0.998
40 -0.06246 0.062428 -0.007826 -0.001319 -0.10450 1.039
41 -0.09562 0.052504 0.005169 0.017290 -0.12679 1.014
42 -0.21697 -0.232289 0.094774 0.098850 -0.31600 0.920
43 -0.08283 0.099258 -0.052551 0.025986 -0.13382 1.043
44 -0.01245 0.007480 -0.018080 0.003914 -0.02237 1.078
45 0.12395 -0.085904 0.130785 -0.083373 0.17985 1.045
46 0.02184 -0.003768 -0.033403 0.016642 0.05859 1.065
47 -0.05276 0.159987 -0.029643 -0.074587 -0.21663 1.034
48 -0.05420 0.076911 -0.054360 0.030191 -0.09678 1.084
49 0.20718 -0.118156 0.068838 -0.094258 0.24439 0.923
50 0.03966 0.046688 -0.027931 -0.026229 0.05998 1.081
51 -0.13723 0.134517 -0.112448 0.085385 -0.20048 1.030
52 0.03663 0.000954 -0.381573 0.329041 0.60274 0.867
53 -0.00932 -0.003098 0.043090 0.060856 0.08956 1.163
54 0.03745 0.101964 -0.030357 0.026719 0.13153 1.077
55 0.02933 0.040344 0.062201 0.083310 0.17670 1.054
56 0.00752 0.012394 -0.005119 -0.001979 0.01485 1.083
57 0.00494 0.003285 -0.005257 -0.002290 0.00731 1.072
58 -0.01705 -0.008225 0.159026 -0.126702 -0.24081 1.063
59 -0.04542 0.107133 0.041502 -0.105497 -0.22307 1.018
60 0.08006 0.094485 -0.419463 0.218064 0.54541 0.894
61 0.01089 0.032514 -0.150528 -0.150288 -0.25197 1.121
62 0.02319 -0.111151 -0.010246 0.097280 0.18766 1.057
63 0.08061 0.089413 -0.026166 -0.024899 0.12512 1.042
64 0.22687 -0.308988 0.240957 -0.152440 0.40011 0.982
65 0.07488 0.007001 0.177833 0.117264 0.31642 0.975
66 0.09805 -0.076394 0.076848 -0.064087 0.13235 1.051
67 0.02456 -0.031181 0.166663 0.120283 0.25777 1.062
68 -0.13371 -0.096308 0.115798 0.082014 -0.18121 1.026
69 0.09481 -0.065885 0.081749 -0.064296 0.12800 1.055
70 0.05898 -0.143413 0.008126 0.077114 0.21626 1.019
71 0.01182 0.009145 0.002079 -0.000936 0.01879 1.063
72 -0.06763 -0.076379 0.057596 0.054239 -0.10311 1.090
73 0.00102 0.003319 0.002190 0.005213 0.00987 1.095
74 0.08592 0.000247 -0.147223 -0.307552 -0.39291 1.231
75 -0.05821 -0.039144 0.051499 0.033110 -0.07902 1.062
76 0.12495 0.012482 0.024325 -0.064766 0.12912 1.010
77 0.20754 -0.260459 0.127618 -0.052088 0.34762 0.894
78 -0.17737 0.212606 -0.154484 0.098645 -0.28516 0.993
79 -0.21268 -0.243349 0.153181 0.146893 -0.31753 0.982
80 -0.08280 -0.050622 -0.041949 -0.008647 -0.14831 1.019
81 0.03024 0.034308 -0.021274 -0.020529 0.04487 1.083
82 -0.10730 -0.077515 0.048488 0.065721 -0.12994 1.036
83 0.02947 0.015886 -0.042736 -0.001347 0.05619 1.067
84 -0.01025 -0.006035 -0.016079 0.033204 0.04017 1.309
85 -0.04921 -0.097059 0.038225 0.003394 -0.11510 1.075
86 -0.05982 -0.076989 0.024350 0.014970 -0.10217 1.056
87 -0.15282 0.159347 -0.148686 0.111757 -0.23696 1.042
88 0.07151 0.054958 -0.080770 -0.037504 0.10932 1.061
89 0.24386 0.151791 -0.084195 -0.142089 0.28143 0.907
90 -0.04305 -0.079274 0.024057 -0.004234 -0.10118 1.069
91 0.00600 0.174162 0.038409 -0.217110 -0.33424 1.044
92 -0.06951 0.064238 -0.067281 0.051846 -0.10371 1.080
93 0.06544 0.017081 -0.036167 -0.028075 0.07657 1.045
94 0.03370 0.039461 0.022488 0.029899 0.10008 1.059
95 0.02392 0.088073 0.222652 0.340343 0.58503 0.880
96 -0.08969 0.050613 0.055503 -0.028703 -0.17196 0.998
97 0.02296 -0.018363 0.021359 -0.016483 0.03262 1.083
98 -0.00694 0.006215 -0.007512 0.005512 -0.01068 1.099
99 -0.06262 0.076671 0.044344 -0.064143 -0.18326 1.014
100 -0.08345 -0.068078 0.043390 0.052741 -0.10577 1.052
cook.d hat inf
1 4.35e-03 0.0352
2 2.31e-03 0.0367
3 5.26e-03 0.0230
4 2.64e-03 0.0254
5 3.43e-03 0.0162
6 1.42e-03 0.0197
7 2.20e-04 0.1234 *
8 1.16e-02 0.0159
9 4.82e-03 0.0426
10 9.47e-04 0.0221
11 8.26e-04 0.0180
12 7.95e-04 0.0377
13 1.31e-03 0.0316
14 1.80e-02 0.0327
15 2.38e-02 0.1083 *
16 3.60e-03 0.0445
17 2.96e-04 0.0444
18 1.08e-04 0.0219
19 3.15e-05 0.0412
20 3.17e-07 0.0155
21 1.15e-02 0.0281
22 3.15e-03 0.0500
23 4.42e-03 0.0437
24 7.19e-03 0.0924 *
25 2.36e-03 0.0197
26 3.45e-03 0.0219
27 5.15e-04 0.0172
28 5.21e-03 0.0345
29 2.22e-02 0.0353
30 6.29e-03 0.0252
31 1.70e-03 0.0166
32 9.75e-05 0.0138
33 1.71e-02 0.0355
34 1.28e-02 0.0223
35 6.55e-04 0.0412
36 1.73e-02 0.0150 *
37 2.39e-02 0.0586
38 1.35e-02 0.0642
39 5.48e-03 0.0153
40 2.74e-03 0.0195
41 4.02e-03 0.0154
42 2.43e-02 0.0265
43 4.49e-03 0.0269
44 1.26e-04 0.0333
45 8.10e-03 0.0367
46 8.66e-04 0.0259
47 1.17e-02 0.0390
48 2.36e-03 0.0462
49 1.46e-02 0.0173
50 9.08e-04 0.0391
51 1.00e-02 0.0342
52 8.63e-02 0.0573 *
53 2.03e-03 0.1059 *
54 4.35e-03 0.0461
55 7.83e-03 0.0408
56 5.57e-05 0.0377
57 1.35e-05 0.0277
58 1.45e-02 0.0575
59 1.24e-02 0.0342
60 7.13e-02 0.0548
61 1.59e-02 0.0937
62 8.83e-03 0.0444
63 3.93e-03 0.0247
64 3.93e-02 0.0541
65 2.46e-02 0.0377
66 4.40e-03 0.0308
67 1.66e-02 0.0599
68 8.20e-03 0.0290
69 4.12e-03 0.0321
70 1.16e-02 0.0332
71 8.91e-05 0.0196
72 2.68e-03 0.0509
73 2.46e-05 0.0480
74 3.87e-02 0.1779 *
75 1.57e-03 0.0272
76 4.16e-03 0.0146
77 2.92e-02 0.0267
78 2.01e-02 0.0374
79 2.48e-02 0.0400
80 5.50e-03 0.0205
81 5.08e-04 0.0388
82 4.23e-03 0.0232
83 7.97e-04 0.0272
84 4.08e-04 0.2035 *
85 3.34e-03 0.0421
86 2.63e-03 0.0278
87 1.40e-02 0.0463
88 3.01e-03 0.0322
89 1.92e-02 0.0201
90 2.58e-03 0.0356
91 2.78e-02 0.0656
92 2.71e-03 0.0440
93 1.48e-03 0.0165
94 2.52e-03 0.0289
95 8.16e-02 0.0575
96 7.35e-03 0.0191
97 2.69e-04 0.0380
98 2.88e-05 0.0511
99 8.37e-03 0.0255
100 2.81e-03 0.0262
- there is no obvious patterns in the residuals (first plot), or at least there are no obvious trends remaining that would be indicative of non-linearity or non-homogeneity of variance
- The data do not appear to deviate substantially from normality according to the Q-Q normal plot
- None of the observations are considered overly influential (Cooks' D values not approaching 1).
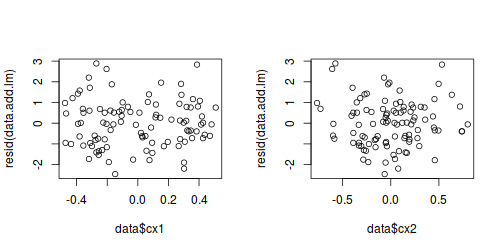
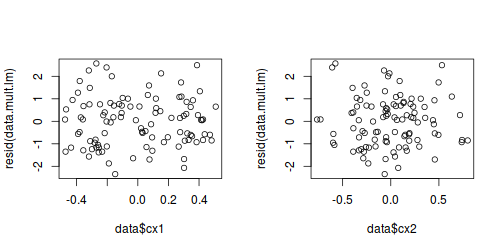
In addition to the above residual plot, in which the residuals are plotted against the fitted (predicted) values, it is also a good idea to plot the residuals against each of the original covariates.
# Additive model par(mfrow = c(1, 2)) plot(data$cx1, resid(data.add.lm)) plot(data$cx2, resid(data.add.lm))
# Multiplicative model par(mfrow = c(1, 2)) plot(data$cx1, resid(data.mult.lm)) plot(data$cx2, resid(data.mult.lm))
## Additive model data.aug = augment(data.add.lm, data) head(data.aug)
# A tibble: 6 x 12
y x1 x2 cx1 cx2 .fitted .se.fit .resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 3.51 0.168 0.901 -0.316 0.0299 2.91 0.201 0.604
2 5.09 0.808 1.33 0.323 0.457 5.44 0.197 -0.346
3 4.04 0.385 0.517 -0.0991 -0.354 3.03 0.171 1.00
4 4.01 0.328 0.974 -0.156 0.103 3.49 0.158 0.513
5 5.38 0.602 1.09 0.118 0.216 4.48 0.135 0.901
6 4.53 0.604 0.824 0.120 -0.0468 4.12 0.135 0.408
# … with 4 more variables: .hat <dbl>, .sigma <dbl>,
# .cooksd <dbl>, .std.resid <dbl>
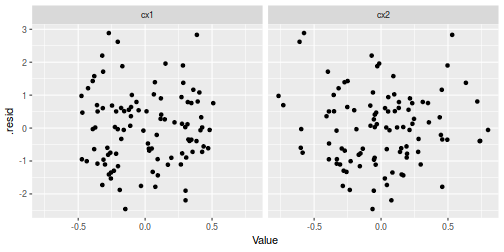
data.aug %>% gather(key = Var, value = Value, cx1, cx2) %>% ggplot(aes(y = .resid, x = Value)) + geom_point() + facet_grid(~Var)
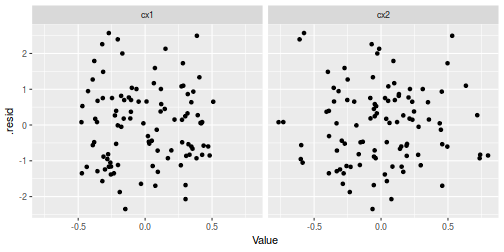
## Multiplicative model augment(data.mult.lm, data) %>% gather(key = Var, value = Value, cx1, cx2) %>% ggplot(aes(y = .resid, x = Value)) + geom_point() + facet_grid(~Var)
Partial effects plots
Finally, we would usually like to visualize the trend(s) graphically so as to help assess the goodness of the model. Since the multiple regression estimates partial effects (effects of one term holding the others constant), graphical summaries are partial effects plots.
Within the effects package, there are a number of functions that can be used to generate partial effects:
- effect(term=, mod=) is used to generate the partial effect of a single term
- allEffect(term=, mod=) is used to generate the partial effects of all effects
- Effect(focal.predictors=, mod=) is used to generate the partial effects of a single predictor across a range of values of the other main effects (thereby showing how the trend in one predictor alters according to the level of the other predictor(s).
Each of these functions returns an eff object that contains the predicted values of $y$ for a range of $x$ values. The effects package also contains a plotting function that takes the eff object and plots it.
The emmeans package also has routines for estimating and plotting the partial effects. Furthermore, there are routines for plotting the partial effects estimated by both emmeans and effects packages as well as the predict function in ggplot. Each of these will be demonstrated below for both the additive and multiplicative models.
- additive model
- single partial effect plot
library(effects) plot(effect("cx1", data.add.lm, partial.residuals = TRUE))

library(ggeffects) ggeffect(data.add.lm, ~cx1) %>% plot

library(ggeffects) ggemmeans(data.add.lm, ~cx1) %>% plot

library(ggeffects) ggpredict(data.add.lm, ~cx1) %>% plot(rawdata = TRUE)

- all partial effect plots
library(effects) plot(allEffects(data.add.lm, partial.residuals = TRUE))

library(ggeffects) library(gridExtra) grid.arrange(ggeffect(data.add.lm, ~cx1) %>% plot, ggeffect(data.add.lm, ~cx2) %>% plot, nrow = 1)

library(ggeffects) library(gridExtra) grid.arrange(ggemmeans(data.add.lm, ~cx1) %>% plot, ggemmeans(data.add.lm, ~cx2) %>% plot, nrow = 1)

library(ggeffects) library(gridExtra) grid.arrange(ggpredict(data.add.lm, ~cx1) %>% plot(rawdata = TRUE), ggpredict(data.add.lm, ~cx2) %>% plot(rawdata = TRUE), nrow = 1)

- single partial effect plot
- multiplicative model
- single partial effect plot
library(effects) plot(effect("cx1", data.mult.lm, partial.residuals = TRUE))

library(ggeffects) ggeffect(data.mult.lm, ~cx1) %>% plot

library(ggeffects) ggemmeans(data.mult.lm, ~cx1) %>% plot

library(ggeffects) ggpredict(data.mult.lm, ~cx1) %>% plot(rawdata = TRUE)

- all partial effect plots
library(effects) plot(allEffects(data.mult.lm, xlevels = 5, partial.residuals = TRUE))

library(ggeffects) ggeffect(data.mult.lm, terms = c("cx1", "cx2 [-1,-0.5,0,0.5,1]")) %>% plot

library(ggeffects) ggemmeans(data.mult.lm, terms = c("cx1", "cx2 [-1,-0.5,0,0.5,1]")) %>% plot

library(ggeffects) ggpredict(data.mult.lm, terms = c("cx1", "cx2 [-1,-0.5,0,0.5,1]")) %>% plot

- interactions in partial effects
library(effects) plot(Effect(focal.predictors = c("cx1", "cx2"), data.mult.lm, partial.residuals = TRUE))

library(ggeffects) ggeffect(data.mult.lm, ~cx1 + cx2) %>% plot

library(ggeffects) ggemmeans(data.mult.lm, ~cx1 + cx2) %>% plot

library(ggeffects) ggpredict(data.mult.lm, ~cx1 + cx2) %>% plot

- single partial effect plot
It is clear from the above figures, that the effect of cx1 on $y$ changes across the range of cx2 (suggestive of an interaction).
You might have noticed that the x-axis on all of the above plots reflects the centered data. Often we would prefer to visualize the effects in terms of the raw data range. That is we wish to back-transform the values into the original scale. Furthermore, they are not overly nice looking figures.
Recall that the purpose of the above figures is to assess the validity of the fitted model and thus scales and aesthetics are not overly critical. We will produce nicer looking figures in Section 8.
Exploring the model parameters, test hypotheses
If there was any evidence that the assumptions had been violated or the model was not an appropriate fit, then we would need to reconsider the model and start the process again. In this case, there is no evidence that the test will be unreliable so we can proceed to explore the test statistics. The main statistic of interest is the t-statistic ($t$) for each of the partial slope parameters.
- additive model
summary(data.add.lm)
Call: lm(formula = y ~ cx1 + cx2, data = data) Residuals: Min 1Q Median 3Q Max -2.45927 -0.78738 -0.00688 0.71051 2.88492 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.8234 0.1131 33.793 < 2e-16 *** cx1 3.0250 0.4986 6.067 2.52e-08 *** cx2 1.3878 0.4281 3.242 0.00163 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1.131 on 97 degrees of freedom Multiple R-squared: 0.5361, Adjusted R-squared: 0.5265 F-statistic: 56.05 on 2 and 97 DF, p-value: < 2.2e-16# OR via confidence intervals of the parameters confint(data.add.lm)
2.5 % 97.5 % (Intercept) 3.5988464 4.047962 cx1 2.0353869 4.014675 cx2 0.5381745 2.237488
## tidy version tidy(data.add.lm, conf.int = TRUE)
# A tibble: 3 x 7 term estimate std.error statistic p.value conf.low conf.high <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 3.82 0.113 33.8 1.86e-55 3.60 4.05 2 cx1 3.03 0.499 6.07 2.52e- 8 2.04 4.01 3 cx2 1.39 0.428 3.24 1.63e- 3 0.538 2.24
Conclusions:
-
At the mean level of cx2 (and thus $x2$), an increase in cx1 (and thus $x1$) is associated with a significant linear increase in $y$.
Every 1 unit increase in $x1$ results in a
3.03unit decrease in $y$. - There is no inferential evidence of a relationship between $y$ and $x2$ (holding $x1 constant).
- The 95% confidence intervals give an indication of the uncertainty in the effect sizes. Confidence bounds that do not contain 0 (zero) suggest evidence that the parameter is 'significantly' different from zero.
- The $R^2$ value is
0.54suggesting that approximately54% of the total variance in $y$ can be explained by its linear relationship with $x1$ and $x2$. The $R^2$ value is thus a measure of the strength of the relationship. - The adjusted $R^2$ value ($R^2$ value penalized according to the number of predictor terms) is
0.53. In multiple linear regression, the adjusted $R^2$ is the more appropriate value for comparing models as it is a measure of the explanitory power given the model complexity.
-
At the mean level of cx2 (and thus $x2$), an increase in cx1 (and thus $x1$) is associated with a significant linear increase in $y$.
Every 1 unit increase in $x1$ results in a
- multiplicative model
summary(data.mult.lm)
Call: lm(formula = y ~ cx1 * cx2, data = data) Residuals: Min 1Q Median 3Q Max -2.34877 -0.85435 0.06905 0.71265 2.57068 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 3.6710 0.1315 27.924 < 2e-16 *** cx1 2.9292 0.4914 5.961 4.15e-08 *** cx2 1.3445 0.4207 3.196 0.00189 ** cx1:cx2 2.6651 1.2305 2.166 0.03281 * --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1.111 on 96 degrees of freedom Multiple R-squared: 0.5577, Adjusted R-squared: 0.5439 F-statistic: 40.35 on 3 and 96 DF, p-value: < 2.2e-16# OR via confidence intervals of the parameters confint(data.mult.lm)
2.5 % 97.5 % (Intercept) 3.4100621 3.931972 cx1 1.9537887 3.904642 cx2 0.5094571 2.179451 cx1:cx2 0.2224680 5.107650
## tidy version tidy(data.mult.lm, conf.int = TRUE)
# A tibble: 4 x 7 term estimate std.error statistic p.value conf.low conf.high <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 3.67 0.131 27.9 7.06e-48 3.41 3.93 2 cx1 2.93 0.491 5.96 4.15e- 8 1.95 3.90 3 cx2 1.34 0.421 3.20 1.89e- 3 0.509 2.18 4 cx1:cx2 2.67 1.23 2.17 3.28e- 2 0.222 5.11
Conclusions:
- There is inferential evidence of a significant interaction implying that the 'effects' of cx1 are non consistent across all levels of cx2 and vice verse. This consistent with what was suggestive in the partial regression plots above..
-
At the mean level of cx2 (and thus $x2$), an increase in cx1 (and thus $x1$) is associated with a significant linear increase in $y$.
Every 1 unit increase in $x1$ results in a
2.93unit decrease in $y$. - There is no inferential evidence of a relationship between $y$ and $x2$ (holding $x1$ constant).
- The 95% confidence intervals give an indication of the uncertainty in the effect sizes. Confidence bounds that do not contain 0 (zero) suggest evidence that the parameter is 'significantly' different from zero.
- The $R^2$ value is
0.56suggesting that approximately56% of the total variance in $y$ can be explained by its linear relationship with $x1$ and $x2$. The $R^2$ value is thus a measure of the strength of the relationship. - The adjusted $R^2$ value ($R^2$ value penalized according to the number of predictor terms) is
0.54. In multiple linear regression, the adjusted $R^2$ is the more appropriate value for comparing models as it is a measure of the explanitory power given the model complexity.
Exploring interactions (statistically)
The nature of significant interactions (e.g. cx1 and cx2 on Y) can be further explored by re-fitting the multiple linear model to explore the partial effects of one of the predictor variables (e.g. cx1 ) for a specific set of levels of the other interacting predictor variable(s) (e.g. the mean of cx2 as well as this mean $\pm$ 1 and or 2 standard deviations). For such subsequent main effects tests, ignore the effect of the interaction, which will be identical to that previously tested, and focus purely on the individual partial slope ($\beta_1$).
In the absence of any other criterion to split the analysis up, we will explore the effects of $cx1$ at 5 different levels of $cx2$ (the mean level as well as 1 and 2 standard deviations above and below the mean).
The first step in the process is to calculate a constant for each of the five levels that represents the value to add to the mean to center the data around the new level.
# 2 standard deviations below the mean (M2 <- mean(data$cx2) - 2 * sd(data$cx2))
[1] -0.667053
# 1 standard deviation below the mean (M1 <- mean(data$cx2) - 1 * sd(data$cx2))
[1] -0.3335265
# mean longitude (M <- mean(data$cx2))
[1] -1.500048e-17
# 1 standard deviation above the mean (P1 <- mean(data$cx2) + 1 * sd(data$cx2))
[1] 0.3335265
# 2 standard deviation below the mean longitude (P2 <- mean(data$cx2) + 2 * sd(data$cx2))
[1] 0.667053
(m2 <- summary(data.lmM2 <- lm(y ~ cx1 * c(cx2 - M2), data = data))$coef["cx1", ])
Estimate Std. Error t value Pr(>|t|) 1.1514799 0.9939162 1.1585282 0.2495225
(m1 <- summary(data.lmM2 <- lm(y ~ cx1 * c(cx2 - M1), data = data))$coef["cx1", ])
Estimate Std. Error t value Pr(>|t|) 2.040347707 0.668005930 3.054385621 0.002918947
(m <- summary(data.lmM2 <- lm(y ~ cx1 * c(cx2 - M), data = data))$coef["cx1", ])
Estimate Std. Error t value Pr(>|t|) 2.929216e+00 4.914028e-01 5.960926e+00 4.149832e-08
(p1 <- summary(data.lmM2 <- lm(y ~ cx1 * c(cx2 - P1), data = data))$coef["cx1", ])
Estimate Std. Error t value Pr(>|t|) 3.818083e+00 6.112313e-01 6.246544e+00 1.145367e-08
(p2 <- summary(data.lmM2 <- lm(y ~ cx1 * c(cx2 - P2), data = data))$coef["cx1", ])
Estimate Std. Error t value Pr(>|t|) 4.706951e+00 9.179395e-01 5.127736e+00 1.521105e-06
rbind(`-2sd` = m2, `-1sd` = m1, `Mean cx2` = m, `+1sd` = p1, `+2sd` = p2)
Estimate Std. Error t value Pr(>|t|) -2sd 1.151480 0.9939162 1.158528 2.495225e-01 -1sd 2.040348 0.6680059 3.054386 2.918947e-03 Mean cx2 2.929216 0.4914028 5.960926 4.149832e-08 +1sd 3.818083 0.6112313 6.246544 1.145367e-08 +2sd 4.706951 0.9179395 5.127736 1.521105e-06
emtrends(data.mult.lm, ~cx1 | cx2, at = list(cx2 = c(M2, M1, M, P1, P2)), var = "cx1") %>% as.data.frame
cx1 cx2 cx1.trend SE df lower.CL upper.CL 1 7.233797e-18 -6.670530e-01 1.151480 0.9939162 96 -0.8214281 3.124388 2 7.233797e-18 -3.335265e-01 2.040348 0.6680059 96 0.7143664 3.366329 3 7.233797e-18 -1.500048e-17 2.929216 0.4914028 96 1.9537887 3.904642 4 7.233797e-18 3.335265e-01 3.818083 0.6112313 96 2.6047988 5.031368 5 7.233797e-18 6.670530e-01 4.706951 0.9179395 96 2.8848557 6.529047
Graphical Summary
- additive model
## define the new prediction values (cx1) data.list = with(data, list(cx1 = seq(min(cx1), max(cx1), len = 100), cx2 = 0)) data.grid = ref_grid(data.add.lm, ~cx1, cov.reduce = FALSE, at = data.list) newdata = confint(data.grid) ## back transform the focal predictor newdata = newdata %>% mutate(x1 = cx1 + mean(data$x1)) ## Calculate the partial residuals presid = ref_grid(data.add.lm, ~cx1, cov.reduce = function(x) x, at = list(cx2 = 0)) %>% predict + as.vector(resid(data.add.lm)) ## convert to data frame and backtransform predictor partial.obs = data.frame(presid = presid, x1 = recover_data(data.add.lm)$cx1 + mean(data$x1)) library(ggplot2) p1 <- ggplot(newdata, aes(y = prediction, x = x1)) + geom_point(data = partial.obs, aes(y = presid), color = "grey") + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) ## same for cx2 data.list = with(data, list(cx2 = seq(min(cx2), max(cx2), len = 100), cx1 = 0)) data.grid = ref_grid(data.add.lm, ~cx2, cov.reduce = FALSE, at = data.list) newdata = confint(data.grid) ## back transform the focal predictor newdata = newdata %>% mutate(x2 = cx2 + mean(data$x2)) ## Calculate the partial residuals presid = ref_grid(data.add.lm, ~cx2, cov.reduce = function(x) x, at = list(cx1 = 0)) %>% predict + as.vector(resid(data.add.lm)) ## convert to data frame and backtransform predictor partial.obs = data.frame(presid = presid, x2 = recover_data(data.add.lm)$cx2 + mean(data$x2)) library(ggplot2) p2 <- ggplot(newdata, aes(y = prediction, x = x2)) + geom_point(data = partial.obs, aes(y = presid), color = "grey") + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X2") + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) library(gridExtra) grid.arrange(p1, p2, ncol = 2)

# for cx1. Generate a sequence of cx1 values to predict and # set cx2 = 0 since this is its mean newdata <- data.frame(cx1 = seq(min(data$cx1), max(data$cx1), len = 100), cx2 = 0) fit <- predict(data.add.lm, newdata = newdata, interval = "confidence") fit <- cbind(newdata, fit) fit$x1 <- fit$cx1 + mean(data$x1) head(fit)
cx1 cx2 fit lwr upr x1 1 -0.4755165 0 2.384952 1.863528 2.906376 0.008566967 2 -0.4655705 0 2.415039 1.902481 2.927597 0.018512978 3 -0.4556245 0 2.445126 1.941398 2.948855 0.028458988 4 -0.4456785 0 2.475213 1.980276 2.970150 0.038404998 5 -0.4357325 0 2.505300 2.019114 2.991486 0.048351008 6 -0.4257865 0 2.535387 2.057909 3.012864 0.058297018
# calculated the partial observed values partial.obs <- data.frame(cx1 = data$cx1, cx2 = 0) partial.obs <- cbind(partial.obs, fit = predict(data.add.lm, newdata = partial.obs)) partial.obs$fit <- partial.obs$fit + resid(data.add.lm) partial.obs$x1 <- partial.obs$cx1 + mean(data$x1) head(partial.obs)
cx1 cx2 fit x1 1 -0.31604197 0 3.471860 0.1680415 2 0.32343291 0 4.455814 0.8075164 3 -0.09914114 0 4.527990 0.3849424 4 -0.15634918 0 3.863180 0.3277343 5 0.11801718 0 5.081808 0.6021007 6 0.12031056 0 4.595068 0.6043941
library(ggplot2) p1 <- ggplot(fit, aes(y = fit, x = x1)) + geom_point(data = partial.obs, color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) # for cx2. Generate a sequence of cx2 values to predict and # set cx1 = 0 since this is its mean newdata <- data.frame(cx2 = seq(min(data$cx2), max(data$cx2), len = 100), cx1 = 0) fit <- predict(data.add.lm, newdata = newdata, interval = "confidence") fit <- cbind(newdata, fit) fit$x2 <- fit$cx2 + mean(data$x2) head(fit)
cx2 cx1 fit lwr upr x2 1 -0.7657351 0 2.760693 2.072418 3.448968 0.1051730 2 -0.7499253 0 2.782634 2.107043 3.458226 0.1209829 3 -0.7341154 0 2.804576 2.141639 3.467513 0.1367927 4 -0.7183056 0 2.826517 2.176203 3.476831 0.1526026 5 -0.7024957 0 2.848459 2.210734 3.486183 0.1684125 6 -0.6866859 0 2.870400 2.245230 3.495570 0.1842223
# calculated the partial observed values partial.obs <- data.frame(cx2 = data$cx2, cx1 = 0) partial.obs <- cbind(partial.obs, fit = predict(data.add.lm, newdata = partial.obs)) partial.obs$fit <- partial.obs$fit + resid(data.add.lm) partial.obs$x2 <- partial.obs$cx2 + mean(data$x2) head(partial.obs)
cx2 cx1 fit x2 1 0.02986272 0 4.469341 0.9007709 2 0.45723717 0 4.111988 1.3281453 3 -0.35382350 0 4.336848 0.5170847 4 0.10322304 0 4.479398 0.9741312 5 0.21607055 0 5.024672 1.0869787 6 -0.04683372 0 4.166128 0.8240744
library(ggplot2) p2 <- ggplot(fit, aes(y = fit, x = x2)) + geom_point(data = partial.obs, color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X2") + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) library(gridExtra) grid.arrange(p1, p2, ncol = 2)

# for cx1. Generate a sequence of cx1 values to predict and # set cx2 = 0 since this is its mean newdata <- data.frame(cx1 = seq(min(data$cx1), max(data$cx1), len = 100), cx2 = 0) Xmat = model.matrix(~cx1 + cx2, data = newdata) coefs = coef(data.add.lm) fit = as.vector(coefs %*% t(Xmat)) se = sqrt(diag(Xmat %*% vcov(data.add.lm) %*% t(Xmat))) q = qt(0.975, df = df.residual(data.add.lm)) fit = data.frame(fit = fit, lwr = fit - q * se, upr = fit + q * se) %>% mutate(x1 = newdata$cx1 + mean(data$x1)) ## partial residuals newdata <- data.frame(cx1 = data$cx1, cx2 = 0) Xmat = model.matrix(~cx1 + cx2, data = newdata) coefs = coef(data.add.lm) presid = as.vector(coefs %*% t(Xmat)) partial.obs = data.frame(presid = presid + resid(data.add.lm)) %>% mutate(x1 = newdata$cx1 + mean(data$x1)) library(ggplot2) p1 <- ggplot(fit, aes(y = fit, x = x1)) + geom_point(data = partial.obs, aes(y = presid), color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) ## now for cx2 newdata <- data.frame(cx2 = seq(min(data$cx2), max(data$cx2), len = 100), cx1 = 0) Xmat = model.matrix(~cx1 + cx2, data = newdata) coefs = coef(data.add.lm) fit = as.vector(coefs %*% t(Xmat)) se = sqrt(diag(Xmat %*% vcov(data.add.lm) %*% t(Xmat))) q = qt(0.975, df = df.residual(data.add.lm)) fit = data.frame(fit = fit, lwr = fit - q * se, upr = fit + q * se) %>% mutate(x2 = newdata$cx2 + mean(data$x2)) ## partial residuals newdata <- data.frame(cx2 = data$cx2, cx1 = 0) Xmat = model.matrix(~cx1 + cx2, data = newdata) coefs = coef(data.add.lm) presid = as.vector(coefs %*% t(Xmat)) partial.obs = data.frame(presid = presid + resid(data.add.lm)) %>% mutate(x2 = newdata$cx2 + mean(data$x2)) library(ggplot2) p2 <- ggplot(fit, aes(y = fit, x = x2)) + geom_point(data = partial.obs, aes(y = presid), color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X2") + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) library(gridExtra) grid.arrange(p1, p2, ncol = 2)

- multiplicative model
## for cx1. Generate a sequence of cx1 values to predict and ## set cx2 to be equal to the mean and 1 and 2 standard ## deviations above and below the mean data.list = with(data, list(cx1 = seq(min(cx1), max(cx1), len = 100), cx2 = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2))) data.grid = ref_grid(data.mult.lm, ~cx1 | cx2, at = data.list, cov.reduce = function(x) x) newdata = confint(data.grid) ## back transform the focal predictor newdata = newdata %>% mutate(x1 = cx1 + mean(data$x1)) ## Calculate the partial residuals presid = ref_grid(data.mult.lm, ~cx1, cov.reduce = function(x) x, at = list(cx2 = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2))) %>% summary %>% mutate(presid = prediction + as.vector(resid(data.mult.lm))) ## convert to data frame and backtransform predictor partial.obs = presid %>% mutate(presid = presid + resid(data.mult.lm), x1 = cx1 + mean(data$x1), x2 = cx2 + mean(data$x2)) library(ggplot2) p1 <- ggplot(newdata, aes(y = prediction, x = x1, group = factor(cx2), fill = factor(cx2), color = factor(cx2))) + geom_point(data = partial.obs, aes(y = presid), alpha = 0.2) + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), color = NA, alpha = 0.2) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + scale_fill_discrete("X2", breaks = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2), labels = lapply(-2:2, function(i) bquote(.(i) * sigma))) + scale_color_discrete("X2", breaks = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2), labels = lapply(-2:2, function(i) bquote(.(i) * sigma))) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) # for cx2. Generate a sequence of cx2 values to predict and # set cx1 = 0 since this is its mean newdata$ccx2 <- factor(newdata$cx2, labels = paste("X2:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$ccx2 <- factor(partial.obs$cx2, labels = paste("X2:~", c(-2, -1, 0, 1, 2), "*sigma")) p2 <- ggplot(newdata, aes(y = prediction, x = x1)) + geom_point(data = partial.obs, aes(y = presid)) + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + facet_grid(~ccx2, labeller = label_parsed) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank()) library(gridExtra) grid.arrange(p1, p2, ncol = 1)

## for cx1. Generate a sequence of cx1 values to predict and ## set cx2 to be equal to the mean and 1 and 2 standard ## deviations above and below the mean newdata <- expand.grid(cx1 = seq(min(data$cx1), max(data$cx1), len = 100), cx2 = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2)) fit <- predict(data.mult.lm, newdata = newdata, interval = "confidence") fit <- cbind(newdata, fit) fit$x1 <- fit$cx1 + mean(data$x1) head(fit)
cx1 cx2 fit lwr upr x1 1 -0.4755165 -0.667053 2.226647 1.357498 3.095796 0.008566967 2 -0.4655705 -0.667053 2.238100 1.384078 3.092122 0.018512978 3 -0.4556245 -0.667053 2.249552 1.410471 3.088634 0.028458988 4 -0.4456785 -0.667053 2.261005 1.436668 3.085342 0.038404998 5 -0.4357325 -0.667053 2.272458 1.462658 3.082257 0.048351008 6 -0.4257865 -0.667053 2.283910 1.488429 3.079391 0.058297018
# calculated the partial observed values partial.obs <- expand.grid(cx1 = data$cx1, cx2 = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2)) partial.obs <- cbind(partial.obs, fit = predict(data.mult.lm, newdata = partial.obs)) partial.obs$fit <- partial.obs$fit + resid(data.mult.lm) partial.obs$x1 <- partial.obs$cx1 + mean(data$x1) head(partial.obs)
cx1 cx2 fit x1 1 -0.31604197 -0.667053 3.163325 0.1680415 2 0.32343291 -0.667053 2.609724 0.8075164 3 -0.09914114 -0.667053 3.698581 0.3849424 4 -0.15634918 -0.667053 3.291794 0.3277343 5 0.11801718 -0.667053 3.916596 0.6021007 6 0.12031056 -0.667053 3.497351 0.6043941
library(ggplot2) p1 <- ggplot(fit, aes(y = fit, x = x1, group = factor(cx2), fill = factor(cx2), color = factor(cx2))) + geom_point(data = partial.obs, alpha = 0.2) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + scale_fill_discrete("X2", breaks = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2), labels = lapply(-2:2, function(i) bquote(.(i) * sigma))) + scale_color_discrete("X2", breaks = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2), labels = lapply(-2:2, function(i) bquote(.(i) * sigma))) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) # for cx2. Generate a sequence of cx2 values to predict and # set cx1 = 0 since this is its mean fit$ccx2 <- factor(fit$cx2, labels = paste("X2:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$ccx2 <- factor(partial.obs$cx2, labels = paste("X2:~", c(-2, -1, 0, 1, 2), "*sigma")) p2 <- ggplot(fit, aes(y = fit, x = x1)) + geom_point(data = partial.obs) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + facet_grid(~ccx2, labeller = label_parsed) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank()) library(gridExtra) grid.arrange(p1, p2, ncol = 1)

# for cx1. Generate a sequence of cx1 values to predict and # set cx2 = 0 since this is its mean newdata <- expand.grid(cx1 = seq(min(data$cx1), max(data$cx1), len = 100), cx2 = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2)) Xmat = model.matrix(~cx1 * cx2, data = newdata) coefs = coef(data.mult.lm) fit = as.vector(coefs %*% t(Xmat)) se = sqrt(diag(Xmat %*% vcov(data.mult.lm) %*% t(Xmat))) q = qt(0.975, df = df.residual(data.mult.lm)) fit = data.frame(fit = fit, lwr = fit - q * se, upr = fit + q * se) %>% mutate(cx2 = newdata$cx2, x1 = newdata$cx1 + mean(data$x1), x2 = newdata$cx2 + mean(data$x2)) ## partial residuals newdata <- expand.grid(cx1 = data$cx1, cx2 = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2)) Xmat = model.matrix(~cx1 * cx2, data = newdata) coefs = coef(data.mult.lm) presid = as.vector(coefs %*% t(Xmat)) partial.obs = data.frame(presid = presid + rep(resid(data.mult.lm), 5)) %>% mutate(cx2 = newdata$cx2, x1 = newdata$cx1 + mean(data$x1), x2 = newdata$cx2 + mean(data$x2)) library(ggplot2) p1 <- ggplot(fit, aes(y = fit, x = x1, group = factor(cx2), fill = factor(cx2), color = factor(cx2))) + geom_point(data = partial.obs, aes(y = presid), alpha = 0.2) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + scale_fill_discrete("X2", breaks = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2), labels = lapply(-2:2, function(i) bquote(.(i) * sigma))) + scale_color_discrete("X2", breaks = mean(data$cx2) + sd(data$cx2) * c(-2, -1, 0, 1, 2), labels = lapply(-2:2, function(i) bquote(.(i) * sigma))) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) # for cx2. Generate a sequence of cx2 values to predict and # set cx1 = 0 since this is its mean fit$ccx2 <- factor(fit$cx2, labels = paste("X2:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$ccx2 <- factor(partial.obs$cx2, labels = paste("X2:~", c(-2, -1, 0, 1, 2), "*sigma")) p2 <- ggplot(fit, aes(y = fit, x = x1)) + geom_point(data = partial.obs, aes(y = presid)) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous("Y") + scale_x_continuous("X1") + facet_grid(~ccx2, labeller = label_parsed) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank()) library(gridExtra) grid.arrange(p1, p2, ncol = 1)

Model Selection
Not all the predictor variables in a multiple linear model necessarily contribute substantially to explaining variation in the response variable. Those that do not, are unlikely to have much biological impact on the response and therefore could be ommitted from the final regression equation (along with all the other unmeasured variables).
Furthermore, we may wish to determine which of a range of linear and non-linear models best fits the collected data. For the purpose of explaining a response variable, the 'best' regression model is arguably the model that contains only a subset combination of important predictor variables and is therefore the model that explains the most amount of response variability with the fewest predictor terms (parsimony). Typically, the 'best' model will contain the fewest predictor variables as greater numbers of extraneous predictor variables increases the model complexity and sources of uncertainty and thus decreases the precision of resulting predictions.
There are several criteria that can be used to assess the efficiency or fit of a model that are penalized by the number of predictor terms. These criteria are calculated and compared for a set of competing models thereby providing an objective basis on which to select the 'best' regression model.
- $MS_{residuals}$
- represents the mean amount of variation unexplained by the model, and therefore the lowest value indicates the best fit.
- $Adjusted~r^2$
- (the proportion of mean amount of variation in response variable explained and is therefore adjusted for both sample by the model) is calculated as $adj. r_2 = \frac{MS_{residual}}{MS_{total}}$ size and the number of terms. Larger values indicate better fit. Adjusted $r_2$ and $MS_{residuals}$ should not be used to compare between linear and non-linear models
- $Mallow's~C_p$
- is an index resulting from the comparison of the specific model to a model that contain all the possible terms. Models with the lowest value and/or values closest to their respective $p$ (the number of model terms, including the y-intercept) indicate best fit.
- $Akaike~Information~Criteria~(AIC)$
- there are several different versions of AIC, each of which adds a different constant (designed to penalize according to the number of parameters and sample size) to a likelhood function to produce a relative measure of the information content of a model. Smaller values indicate more parsimonious models. As a rule of thumb, if the difference between two AIC values (delta AIC) is greater than 2, the lower AIC is a significant improvement in parsimony.
- $Schwarz~Bayesian~Information~Criteria~(BIC~or~SIC)$
- is outwardly similar to AIC. The constant added to the likelihood function penalizes models with more predictor terms more heavily (and thus select more simple models) than AIC. It is for this reason that BIC is favored by many workers, however, others argue strongly in favor of AIC claiming that the theoretical basis for BIC may not be relevant for most biological applications. The original basis for BIC was for situations in which there were either no effects or else there were a mixture of major and no effects with no intermediate or tapering effects. Furthermore, it assumes that the true model (against which all others are compared) is among the set being assessed.
We will use the dredge() function within the MuMIn package to fit all combinations of models and then rank all the models on the basis of AICc. AICc is AIC corrected for small sample sizes. Note, for more recent versions of MuMIn, it is necessary that the model be fit with na.action=na.fail.
library(MuMIn) data.mult.lm <- lm(y ~ cx1 * cx2, data, na.action = na.fail) dredge(data.mult.lm, rank = "AICc", trace = TRUE)
0 : lm(formula = y ~ 1, data = data, na.action = na.fail) 1 : lm(formula = y ~ cx1 + 1, data = data, na.action = na.fail) 2 : lm(formula = y ~ cx2 + 1, data = data, na.action = na.fail) 3 : lm(formula = y ~ cx1 + cx2 + 1, data = data, na.action = na.fail) 7 : lm(formula = y ~ cx1 + cx2 + cx1:cx2 + 1, data = data, na.action = na.fail)
Global model call: lm(formula = y ~ cx1 * cx2, data = data, na.action = na.fail) --- Model selection table (Int) cx1 cx2 cx1:cx2 df logLik AICc delta weight 8 3.671 2.929 1.344 2.665 5 -150.334 311.3 0.00 0.779 4 3.823 3.025 1.388 4 -152.719 313.9 2.55 0.217 2 3.823 4.003 3 -157.863 322.0 10.67 0.004 3 3.823 2.958 3 -168.803 343.9 32.55 0.000 1 3.823 2 -191.124 386.4 75.07 0.000 Models ranked by AICc(x)
The model with the lowest (=best) AICc was the full model (model containing $cx1$, $cx2$ as well as the interaction). The next best model (comprising the additive effects of $cx1$ and $cx2$), is more than 2 AICc units greater than the best model, and thus we would consider the full model the best.
The model selection table also includes delta and weight columns that indicate the difference in AICc between each successive model and the best model and weigths that can be used in model averaging.
Exhaustive model exploration is increasingly critisized as a 'fishing experdition'. In particular, it is argued that mathematically, some models will come out as 'statistically' more parsimonious than other models. This does not guarantee that these models are ecologically important. Rather, they could be just an artifact of the specific combination of (perhaps slightly unusual) data and simplistic the statistical model. Recall that all models are gross oversimplifactions.
The more modern approach is to proffer up a select (<: 15) candidate models that each encapsulate some plausible response-predictor mechanisms and explore (via information criterion) the relative statistical strength of each of these candidates. This helps ensure that the selected models do have some ecological grounding. It is an acknowledgement of whilst no model is correct, some might provide some useful insighs into a complex ecological system.
Model averaging
Typically, there are multiple plausible alternative models that incorporate different combinations of predictor variables and that yield similar degrees of fit (based on AIC, AICc, QAIC, BIC, etc). Each alternative model will result in different parameter estimates for the predictor variables. Furthermore, conclusions about the relative importance of each of the predictor variables is likely to be dependent on which model is selected.
Model averaging is a technique that calculates weighted averages of the parameter estimates for each predictor variable across a range of possible models (usually models yielding deltas within a certain range - typically 4 units of AIC). In so doing, model selection uncertainty can be incorporated into estimates of parameter precision. Furthermore, through model averaging, we are able to obtain an estimate the relative importance of each of the predictor variables on the the response.
library(MuMIn) data.mult.lm <- lm(y ~ cx1 * cx2, data = data, na.action = na.fail) ma <- model.avg(get.models(dredge(data.mult.lm, rank = "AICc"), subset = delta <= 4)) ma
Call:
model.avg(object = get.models(dredge(data.mult.lm, rank = "AICc"),
subset = delta <= 4))
Component models:
'123' '12'
Coefficients:
(Intercept) cx1 cx2 cx1:cx2
full 3.704258 2.950116 1.353916 2.083722
subset 3.704258 2.950116 1.353916 2.665059
importance(ma)
cx1 cx2 cx1:cx2 Sum of weights: 1.00 1.00 0.78 N containing models: 2 2 1
summary(ma)
Call:
model.avg(object = get.models(dredge(data.mult.lm, rank = "AICc"),
subset = delta <= 4))
Component model call:
lm(formula = y ~ <2 unique rhs>, data = data, na.action = na.fail)
Component models:
df logLik AICc delta weight
123 5 -150.33 311.31 0.00 0.78
12 4 -152.72 313.86 2.55 0.22
Term codes:
cx1 cx2 cx1:cx2
1 2 3
Model-averaged coefficients:
(full average)
Estimate Std. Error Adjusted SE z value Pr(>|z|)
(Intercept) 3.7043 0.1424 0.1438 25.756 < 2e-16 ***
cx1 2.9501 0.4946 0.5008 5.890 < 2e-16 ***
cx2 1.3539 0.4227 0.4280 3.163 0.00156 **
cx1:cx2 2.0837 1.5477 1.5575 1.338 0.18093
(conditional average)
Estimate Std. Error Adjusted SE z value Pr(>|z|)
(Intercept) 3.7043 0.1424 0.1438 25.756 < 2e-16 ***
cx1 2.9501 0.4946 0.5008 5.890 < 2e-16 ***
cx2 1.3539 0.4227 0.4280 3.163 0.00156 **
cx1:cx2 2.6651 1.2305 1.2462 2.138 0.03248 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
With a delta of $<=4$, only the first two models are included for this fabricated example. The above output produces two alternative model averaging outcomes:
- full average in which averages are generated assuming that the term is present in all models. When it is not present, it is given an estimate of 0. Hence, in the above example, the model average estimate for the interaction (cx1:cs2) is weighted.mean(c(2.665,0), w=c(0.779,0.217)). full average is considered a form of shrinkage estimator.
- conditional average in which averages for a model term are only calculated from instances where it is present. Conditional averages are thought to bias the estimates away from zero
Candidate models
The above approaches of naively exploring all possible combinations of models have been criticized as 'fishing' expeditions. It is argued that the very nature of frequentist statistics means that with enough tests, at least some combinations of predictors will appear to fit the data well (or even significantly). As this is just an inevitable artifact of the fact that there are a large number of possible model combinations, then the entire exercise is fundamentally flawed.
Opponents argue that a better approach is to propose a set of up to 10-15 a priori candidate models each of which represents a sensible ecological interpretation. These and only these models are compared. Furthermore, rather than necessarily isolating a single 'best' model, this approach advocates potentially discussing the 'best' couple or few models - particularly if they are distinct from one another in their predictor constituents.
Worked Examples
- Logan (2010) - Chpt 9
- Quinn & Keough (2002) - Chpt 6
Multiple Linear Regression
Paruelo & Lauenroth (1996) analyzed the geographic distribution and the effects of climate variables on the relative abundance of a number of plant functional types (PFT's) including shrubs, forbs, succulents (e.g. cacti), C3 grasses and C4 grasses. They used data from 73 sites across temperate central North America (see pareulo.syd) and calculated the relative abundance of C3 grasses at each site as a response variable
Download Paruelo data set| Format of paruelo.csv data file | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
paruelo <- read.table("../downloads/data/paruelo.csv", header = T, sep = ",", strip.white = T) head(paruelo)
C3 LAT LONG MAP MAT JJAMAP DJFMAP 1 0.65 46.40 119.55 199 12.4 0.12 0.45 2 0.65 47.32 114.27 469 7.5 0.24 0.29 3 0.76 45.78 110.78 536 7.2 0.24 0.20 4 0.75 43.95 101.87 476 8.2 0.35 0.15 5 0.33 46.90 102.82 484 4.8 0.40 0.14 6 0.03 38.87 99.38 623 12.0 0.40 0.11
- In the table below, list the assumptions of multiple linear regression along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
Assumption Diagnostic/Risk Minimization I. II. III. IV. V.
Q1-2. Construct a scatterplot matrix to investigate these assumptions(HINT)Show scatterplotMatrix (car) codelibrary(car) scatterplotMatrix(~C3 + LAT + LONG + MAP + MAT + JJAMAP + DJFMAP, data = paruelo, diagonal = list(method = "boxplot"))
 Show splom (lattice) code
Show splom (lattice) codelibrary(lattice) splom.lat <- splom(paruelo, type = c("p", "r")) print(splom.lat)
 Show ggpairs (GGally) code
Show ggpairs (GGally) codelibrary(GGally) ggpairs(paruelo, lower = list(continuous = "smooth"), diag = list(continuous = "density"), axisLabels = "none")

- Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?
- C3 abundance is clearly non-normal. Since C3 abundance is relative abundance (which logically must range from 0 to 1),
arguably, the most appropriate approach would be to model these data with a binomial (or perhaps beta) distribution.
Indeed, this is the approach that we will take in Tutorial 10.4 and Tutorial 10.5a
A more simplistic approach that can be applied within simple OLS regression, is to attempt to normalize the response variable via a scale transformation.
Since the C3 relative abundances have values of zero, the authors elected to perform a square-root transformation. Generally speaking, this can be a very dangerous course of action if back-transformations from the fitted model are required due to the nature of squaring sets of numbers that are a mixture of negatives and positives or even less than 1 and greater than 1.
This example therefore potentially serves as a good example of the dangers of root transformations. Try applying a temporary square root transformation (HINT). Does this improve some of these specific assumptions (y or n)?
. Whilst in many model fitting and graphing routines are able to perform transformation inline, for more complex examples, it is often advisable to also create transformed versions of variables.
Show scatterplotMatrix (car) codelibrary(car) scatterplotMatrix(~sqrt(C3)+LAT+LONG+MAP+MAT+JJAMAP+log10(DJFMAP), data=paruelo, diagonal=list(method='boxplot'))
 Show ggpairs (GGally) code
Show ggpairs (GGally) codelibrary(GGally) paruelo = paruelo %>% mutate(sqrtC3=sqrt(C3), lDJFMAP=log10(DJFMAP)) ggpairs(subset(paruelo, select=c('sqrtC3','LAT','LONG','MAP','MAT','lDJFMAP')),lower=list(continuous='smooth'), diagonal=list(continuous="density"), axisLabels="none")

- Is there any evidence that the assumption of Collinearity is likely to be violated (y or n)?
- (Multi)collinearity
occurs when one or more of the predictor variables are correlated to the other predictor variables, therefore this assumption can also be examined by calculating the pairwise correlation coefficients between all the predictor variables (HINT). Which predictor variables are highly correlated?
Show code
cor(paruelo[, -1])
LAT LONG MAP MAT JJAMAP DJFMAP sqrtC3 LAT 1.00000000 0.09655281 -0.246505816 -0.838590413 0.07417497 -0.065124848 0.685561202 LONG 0.09655281 1.00000000 -0.733687027 -0.213109100 -0.49155774 0.770743994 -0.023618820 MAP -0.24650582 -0.73368703 1.000000000 0.355090766 0.11225905 -0.404512409 0.001697706 MAT -0.83859041 -0.21310910 0.355090766 1.000000000 -0.08077131 0.001478037 -0.536007103 JJAMAP 0.07417497 -0.49155774 0.112259049 -0.080771307 1.00000000 -0.791540381 -0.053650973 DJFMAP -0.06512485 0.77074399 -0.404512409 0.001478037 -0.79154038 1.000000000 -0.090151384 sqrtC3 0.68556120 -0.02361882 0.001697706 -0.536007103 -0.05365097 -0.090151384 1.000000000 lDJFMAP -0.07720843 0.76030635 -0.399637550 -0.003065519 -0.79235477 0.984628714 -0.071967657 lDJFMAP LAT -0.077208433 LONG 0.760306349 MAP -0.399637550 MAT -0.003065519 JJAMAP -0.792354765 DJFMAP 0.984628714 sqrtC3 -0.071967657 lDJFMAP 1.000000000
- Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?
- Whilst the above diagnostics are useful at identifying potential (Multi)collinearity issues, they do not examine collinearity
directly. (Multi)collinearity can more be diagnosed directly via
tolerance and variance inflation factor (VIF) measures.
- Calculate the VIF values for each of the predictor variables (HINT).
- Calculate the tolerance values for each of the predictor variables (HINT).
Show codelibrary(car) vif(lm(sqrt(paruelo$C3) ~ LAT + LONG + MAP + MAT + JJAMAP + log10(DJFMAP), data = paruelo))
LAT LONG MAP MAT JJAMAP log10(DJFMAP) 3.560103 4.988318 2.794157 3.752353 3.194724 5.467330library(car) 1/vif(lm(sqrt(paruelo$C3) ~ LAT + LONG + MAP + MAT + JJAMAP + log10(DJFMAP), data = paruelo))
LAT LONG MAP MAT JJAMAP log10(DJFMAP) 0.2808908 0.2004684 0.3578897 0.2664995 0.3130161 0.1829046Predictor VIF Tolerance LAT LONG MAP MAT JJAMAP log10(DJFMAP) - Is there any evidence of (multi)collinearity, and if so, which variables are responsible for violations of this assumption?
- Just like Paruelo and Lauenroth (1996), we will fit the multiplicative model for LAT and LONG.
- Write out the full multiplicative model
- Check the assumptions of this linear model. In particular, check collinearity. HINT
Show scatterplotMatrix (car) code
# via car's scatterplotMatrix function library(car) scatterplotMatrix(~sqrt(C3) + LAT + LONG, data = paruelo, diagonal = list(method = "boxplot"))

vif(lm(sqrt(C3) ~ LAT + LONG, data = paruelo))
LAT LONG 1.00941 1.00941
Show ggpairs (GGally) codeggpairs(subset(paruelo, select = c("sqrtC3", "LAT", "LONG")), lower = list(continuous = "smooth"), diag = list(continuous = "density"), axisLabels = "none")

vif(lm(sqrt(C3) ~ LAT + LONG, data = paruelo))
LAT LONG 1.00941 1.00941
- Obviously, this model will violate collinearity.
It is highly likely that LAT and LONG will be related to the LAT:LONG interaction term.
It turns out that if we center the variables, then the individual terms will no longer
be correlated to the interaction.
We can either generate separate centered versions of the LAT and LONG variables ( HINT) and (HINT) or, we can perform this operation inline when fitting the model.
The advantage of centering the variables inline, is that the model will be aware of the scaling procedure and will capture the information necessary to perform the back-transformations. On the downside, this additional information can cause problems for some routines. Consequently, we will generate separate centered versions, yet hope to not have to use them..
Show codeparuelo$cLAT <- as.vector(scale(paruelo$LAT, scale = F)) paruelo$cLONG <- as.vector(scale(paruelo$LONG, scale = F))
- Write out the full multiplicative model
-
Fit a linear multiplicative model on the centered LAT and LONG (HINT)
Show codeparuelo.lm <- lm(sqrt(C3) ~ scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = paruelo) paruelo.lm1 <- lm(sqrt(C3) ~ cLAT * cLONG, data = paruelo) # library(sjmisc) paruelo.lm1 <- lm(sqrt(C3) ~ # center(LAT)*center(LONG), data=paruelo)
- Examine the diagnostic plots (HINT) specially the residual plot to confirm no further evidence of violations of the analysis assumptions
Show base code
# setup a 2x6 plotting device with small margins par(mfrow = c(2, 3), oma = c(0, 0, 2, 0)) plot(paruelo.lm, ask = F, which = 1:6)

influence.measures(paruelo.lm)
Influence measures of lm(formula = sqrt(C3) ~ scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = paruelo) : dfb.1_ dfb.s.LAs.F dfb.s.LOs.F dfb.ss.Fs.F dffit cov.r cook.d hat inf 1 -0.02402 -0.083059 -0.084079 -0.121467 -0.15232 1.379 5.88e-03 0.2347 * 2 -0.02221 -0.064489 -0.040666 -0.073805 -0.09560 1.227 2.32e-03 0.1389 * 3 0.08130 0.134833 0.066766 0.117108 0.18920 1.083 9.00e-03 0.0556 4 0.18842 0.102837 -0.149242 -0.074613 0.27640 0.957 1.87e-02 0.0317 5 -0.06669 -0.070090 0.046655 0.023640 -0.11683 1.091 3.45e-03 0.0448 6 -0.14663 0.020076 0.158421 0.006884 -0.21885 1.001 1.19e-02 0.0305 7 -0.06266 0.095315 -0.006186 0.047476 -0.11206 1.102 3.17e-03 0.0510 8 -0.14641 0.034868 0.221772 -0.071379 -0.30117 1.016 2.25e-02 0.0520 9 -0.03667 0.026450 0.024624 -0.005908 -0.05703 1.088 8.24e-04 0.0317 10 -0.14355 -0.014721 0.043712 0.016311 -0.15090 0.989 5.65e-03 0.0153 11 -0.06802 -0.077774 0.052091 0.030960 -0.12872 1.101 4.19e-03 0.0534 12 -0.09834 0.126501 0.005986 0.046997 -0.15816 1.064 6.29e-03 0.0388 13 0.11115 -0.093743 -0.111372 0.092157 0.24977 1.061 1.56e-02 0.0580 14 0.08474 0.046585 -0.103485 -0.077405 0.16432 1.104 6.81e-03 0.0622 15 -0.10466 0.005614 0.159085 0.003719 -0.19200 1.063 9.25e-03 0.0460 16 0.02997 0.006031 -0.022676 -0.007923 0.03832 1.082 3.72e-04 0.0234 17 -0.22231 -0.242042 -0.256005 -0.259471 -0.46135 0.867 5.07e-02 0.0464 18 -0.15718 -0.195191 -0.167613 -0.197664 -0.33555 0.980 2.77e-02 0.0483 19 -0.03827 0.067695 0.013203 -0.004632 -0.08826 1.133 1.97e-03 0.0703 20 0.14881 0.082543 -0.079749 -0.027279 0.19334 0.993 9.27e-03 0.0238 21 0.02694 -0.052154 0.013621 -0.042509 0.06315 1.184 1.01e-03 0.1064 * 22 0.01333 0.036162 0.002225 0.019532 0.03980 1.165 4.02e-04 0.0911 23 0.03874 -0.041008 -0.026165 0.016163 0.07567 1.106 1.45e-03 0.0475 24 0.18953 -0.068780 -0.263543 0.120259 0.39649 0.949 3.83e-02 0.0522 25 -0.30655 -0.141051 -0.348442 -0.174237 -0.50904 0.721 5.92e-02 0.0333 * 26 -0.01163 0.020739 -0.004288 0.014771 -0.02450 1.151 1.52e-04 0.0797 27 -0.06640 -0.035776 0.047618 0.021757 -0.09331 1.073 2.20e-03 0.0287 28 0.15820 -0.100195 0.156872 -0.087023 0.24687 1.004 1.51e-02 0.0371 29 0.23271 -0.199428 0.178733 -0.171942 0.36130 0.913 3.16e-02 0.0383 30 -0.05886 -0.051722 0.023280 0.001329 -0.08413 1.075 1.79e-03 0.0278 31 0.18206 -0.039000 0.294547 -0.009475 0.34876 0.977 2.98e-02 0.0503 32 0.04158 0.010092 0.004277 0.002215 0.04358 1.068 4.81e-04 0.0147 33 -0.11614 0.057069 -0.084317 0.045564 -0.15421 1.033 5.95e-03 0.0260 34 0.17140 -0.010972 0.149470 0.000787 0.22867 0.961 1.29e-02 0.0241 35 0.16157 -0.063790 0.207065 -0.047488 0.27074 0.999 1.81e-02 0.0405 36 -0.16599 0.051605 0.046986 0.028324 -0.17882 0.964 7.89e-03 0.0163 37 -0.09520 0.123426 -0.073860 0.112439 -0.18180 1.101 8.32e-03 0.0642 38 -0.12248 0.136168 0.016438 0.044325 -0.18258 1.034 8.33e-03 0.0325 39 0.21589 0.005332 0.135038 0.008527 0.25689 0.889 1.59e-02 0.0190 40 -0.15732 -0.003358 -0.079732 -0.002338 -0.17776 0.972 7.81e-03 0.0172 41 -0.08534 0.010451 -0.044041 0.007825 -0.09659 1.047 2.35e-03 0.0177 42 -0.03339 0.004442 -0.028421 0.002067 -0.04413 1.081 4.93e-04 0.0240 43 0.11153 -0.008546 0.093501 -0.001341 0.14632 1.030 5.36e-03 0.0234 44 0.06621 0.080305 -0.003529 0.027570 0.10631 1.074 2.85e-03 0.0321 45 0.14322 0.175378 -0.007707 0.060327 0.23128 0.999 1.33e-02 0.0324 46 0.00242 0.002970 -0.000135 0.001018 0.00392 1.096 3.89e-06 0.0325 47 0.04762 0.057578 -0.003518 0.018818 0.07632 1.084 1.47e-03 0.0321 48 0.09643 0.105320 -0.013197 0.027624 0.14620 1.048 5.37e-03 0.0294 49 0.21782 0.063120 -0.324557 -0.197238 0.43369 0.971 4.59e-02 0.0654 50 -0.00148 0.001425 0.002076 -0.003405 -0.00566 1.218 8.12e-06 0.1296 * 51 -0.00449 0.005425 0.006061 -0.012462 -0.01985 1.262 1.00e-04 0.1598 * 52 0.02355 -0.011871 -0.037630 0.035697 0.06961 1.160 1.23e-03 0.0885 53 -0.00616 0.005595 0.008294 -0.011850 -0.02099 1.190 1.12e-04 0.1093 * 54 0.11316 -0.020147 0.059511 -0.015058 0.12914 1.024 4.18e-03 0.0181 55 0.08401 -0.006408 0.050234 -0.003848 0.09836 1.049 2.44e-03 0.0188 56 0.01263 0.000401 0.008831 0.000749 0.01556 1.081 6.14e-05 0.0203 57 0.23558 0.012600 0.162103 0.017720 0.28935 0.857 2.00e-02 0.0201 58 0.15162 0.005056 0.085545 0.005265 0.17570 0.979 7.64e-03 0.0181 59 -0.10917 0.059550 -0.109799 0.050149 -0.16684 1.050 6.98e-03 0.0349 60 -0.01928 0.010518 -0.019393 0.008857 -0.02947 1.097 2.20e-04 0.0349 61 0.07137 -0.085274 -0.078631 0.125075 0.23769 1.156 1.42e-02 0.1077 62 -0.05053 0.001789 -0.075856 -0.007046 -0.09174 1.096 2.13e-03 0.0434 63 0.00374 0.000609 -0.000752 -0.000272 0.00388 1.076 3.83e-06 0.0148 64 -0.03243 -0.005963 0.008964 0.002938 -0.03431 1.072 2.98e-04 0.0155 65 -0.17360 -0.059882 0.041757 0.006784 -0.19020 0.951 8.89e-03 0.0164 66 -0.21254 -0.161201 0.312816 0.383538 -0.59693 1.136 8.80e-02 0.1617 67 0.05944 0.032095 -0.092820 -0.099439 0.15603 1.217 6.16e-03 0.1367 * 68 -0.03086 0.033212 -0.039691 0.034038 -0.06400 1.142 1.04e-03 0.0743 69 -0.08462 0.114424 -0.120547 0.127015 -0.20622 1.172 1.07e-02 0.1129 70 -0.12444 0.139820 -0.161230 0.144966 -0.26402 1.097 1.75e-02 0.0789 71 -0.09511 0.010274 0.128949 -0.001656 -0.16322 1.063 6.70e-03 0.0398 72 0.01563 0.003182 -0.030673 -0.027216 0.04310 1.251 4.71e-04 0.1534 * 73 -0.06408 -0.180207 0.005698 -0.072658 -0.19407 1.154 9.51e-03 0.0995Show autoplot codeautoplot(paruelo.lm, which = 1:6)

- All the diagnostics seem reasonable and present no indications that the model fitting and resulting hypothesis tests are likely to be unreliable. Complete the following table (HINT).
Show code
summary(paruelo.lm)
Call: lm(formula = sqrt(C3) ~ scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = paruelo) Residuals: Min 1Q Median 3Q Max -0.51312 -0.13427 -0.01134 0.14086 0.38940 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.4282658 0.0234347 18.275 < 2e-16 *** scale(LAT, scale = FALSE) 0.0436937 0.0048670 8.977 3.28e-13 *** scale(LONG, scale = FALSE) -0.0028773 0.0036842 -0.781 0.4375 scale(LAT, scale = FALSE):scale(LONG, scale = FALSE) 0.0022824 0.0007471 3.055 0.0032 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.1991 on 69 degrees of freedom Multiple R-squared: 0.5403, Adjusted R-squared: 0.5203 F-statistic: 27.03 on 3 and 69 DF, p-value: 1.128e-11confint(paruelo.lm)
2.5 % 97.5 % (Intercept) 0.3815148539 0.475016788 scale(LAT, scale = FALSE) 0.0339842271 0.053403155 scale(LONG, scale = FALSE) -0.0102270077 0.004472489 scale(LAT, scale = FALSE):scale(LONG, scale = FALSE) 0.0007920205 0.003772861
tidy(paruelo.lm)
# A tibble: 4 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 0.428 0.0234 18.3 3.79e-28 2 scale(LAT, scale = FALSE) 0.0437 0.00487 8.98 3.28e-13 3 scale(LONG, scale = FALSE) -0.00288 0.00368 -0.781 4.37e- 1 4 scale(LAT, scale = FALSE):scale(LONG, scale = FALSE) 0.00228 0.000747 3.06 3.20e- 3
Coefficient Estimate t-value P-value Intercept cLAT cLONG cLAT:cLONG
- Examine the diagnostic plots (HINT) specially the residual plot to confirm no further evidence of violations of the analysis assumptions
- Examine the partial regression plots of LAT and LONG (HINT).
Show added variable plots (car) code
# via the car package avPlots(paruelo.lm, ask = F, indentify.points = F)

avPlots(paruelo.lm1, ask = F, indentify.points = F)
 Show effects (effects) code
Show effects (effects) codelibrary(effects) plot(allEffects(paruelo.lm, xlevels = 5, partial.residuals = TRUE), ask = F)

plot(allEffects(paruelo.lm1, xlevels = 5, partial.residuals = TRUE), ask = F)
 Show ggeffect (ggeffects) code
Show ggeffect (ggeffects) codelibrary(ggeffects) ## Unfortunately, ggeffect is one of the functions that is unable to properly deal with inline ## centering, hence the need for fitting the model on pre-centered variables. It does however mean, ## that our axes are presented on the centered scaled... ggeffect(paruelo.lm1, ~cLAT | cLONG) %>% plot(facet = TRUE)
 Show ggpredict (ggeffects) code
Show ggpredict (ggeffects) codelibrary(ggeffects) ## Unfortunately, ggpredict is one of the functions that is unable to properly deal with inline ## centering, hence the need for fitting the model on pre-centered variables. It does however mean, ## that our axes are presented on the centered scaled... ggpredict(paruelo.lm1, ~cLAT | cLONG) %>% plot(facet = TRUE)
 Show ggemmeans (ggeffects) code
Show ggemmeans (ggeffects) codelibrary(ggeffects) ggemmeans(paruelo.lm, terms = c("LAT [29:53]", "LONG [90:120 by=7]")) %>% plot(facet = TRUE)

## OR ggemmeans(paruelo.lm1, terms = c("cLAT", "cLONG [n=2]")) %>% plot(facet = TRUE)

There is clearly an interaction between LAT and LONG. This indicates that the degree to which latitude effects the relative abundance of C3 plants depends on longitude and vice versa. The effects plots expressed for Latitude suggest that the relationship between relative C3 abundance and Latitude increases with increasing Longitude. The effects plots expressed for Longitude suggest that the relationship between relative C3 abundance and Longitude switch from negative at low Latitudes to positive at high Latitudes.
- To investigate these patterns further, we will examine the simple effects of latitude at a specific range of longitudes. The levels of longitude that we will use are the mean longitude value as well as the mean plus or minus 1 SD and plus or minus 2 SD.
- Calculate the five levels of longitude on which the simple effects of latitude will be investigated. (HINT, HINT, etc).
Show code
# 2 standard deviations below the mean longitude LongM2 <- mean(paruelo$cLONG) - 2 * sd(paruelo$cLONG) # 1 standard deviation below the mean longitude LongM1 <- mean(paruelo$cLONG) - 1 * sd(paruelo$cLONG) # mean longitude LongM <- mean(paruelo$cLONG) # 1 standard deviation above the mean longitude LongP1 <- mean(paruelo$cLONG) + 1 * sd(paruelo$cLONG) # 2 standard deviation below the mean longitude LongP2 <- mean(paruelo$cLONG) + 2 * sd(paruelo$cLONG)
- Calculate the five levels of longitude on which the simple effects of latitude will be investigated. (HINT, HINT, etc).
- Investigate the simple effects of latitude on the relative abundance of C3 plants for each of these levels of longitude. (HINT), (HINT), etc).
Show emtrends code
emtrends(paruelo.lm1, ~cLAT | cLONG, at = list(cLONG = c(LongM2, LongM1, LongM, LongP1, LongP2)), var = "cLAT") %>% as.data.frame
cLAT cLONG cLAT.trend SE df lower.CL upper.CL 1 3.89291e-16 -1.287083e+01 0.01431678 0.008837028 69 -0.003312612 0.03194616 2 3.89291e-16 -6.435417e+00 0.02900523 0.005270175 69 0.018491523 0.03951894 3 3.89291e-16 -6.424270e-15 0.04369369 0.004867032 69 0.033984227 0.05340316 4 3.89291e-16 6.435417e+00 0.05838215 0.008113745 69 0.042195671 0.07456863 5 3.89291e-16 1.287083e+01 0.07307061 0.012418103 69 0.048297168 0.09784404
Show manual codeLatM2 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongM2), data = paruelo))$coef["cLAT", ] LatM1 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongM1), data = paruelo))$coef["cLAT", ] LatM <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongM), data = paruelo))$coef["cLAT", ] LatP1 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongP1), data = paruelo))$coef["cLAT", ] LatP2 <- summary(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongP2), data = paruelo))$coef["cLAT", ] rbind(`Lattitude at Long-2sd` = LatM2, `Lattitude at Long-1sd` = LatM1, `Lattitude at mean Long` = LatM, `Lattitude at Long+1sd` = LatP1, `Lattitude at Long+2sd` = LatP2)
Estimate Std. Error t value Pr(>|t|) Lattitude at Long-2sd 0.01431678 0.008837028 1.620090 1.097748e-01 Lattitude at Long-1sd 0.02900523 0.005270175 5.503657 5.926168e-07 Lattitude at mean Long 0.04369369 0.004867032 8.977481 3.279384e-13 Lattitude at Long+1sd 0.05838215 0.008113745 7.195463 5.877401e-10 Lattitude at Long+2sd 0.07307061 0.012418103 5.884200 1.301574e-07
# or via confidence intervals LatM2 <- confint(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongM2), data = paruelo))["cLAT", ] LatM1 <- confint(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongM1), data = paruelo))["cLAT", ] LatM <- confint(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongM), data = paruelo))["cLAT", ] LatP1 <- confint(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongP1), data = paruelo))["cLAT", ] LatP2 <- confint(paruelo.lmM2 <- lm(sqrt(C3) ~ cLAT * c(cLONG - LongP2), data = paruelo))["cLAT", ] rbind(`Lattitude at Long-2sd` = LatM2, `Lattitude at Long-1sd` = LatM1, `Lattitude at mean Long` = LatM, `Lattitude at Long+1sd` = LatP1, `Lattitude at Long+2sd` = LatP2)
2.5 % 97.5 % Lattitude at Long-2sd -0.003312612 0.03194616 Lattitude at Long-1sd 0.018491523 0.03951894 Lattitude at mean Long 0.033984227 0.05340316 Lattitude at Long+1sd 0.042195671 0.07456863 Lattitude at Long+2sd 0.048297168 0.09784404
- Finally, lets have a summary figure (or two).
Show predict code
newdata <- expand.grid(LAT = seq(min(paruelo$LAT), max(paruelo$LAT), len = 100), LONG = mean(paruelo$LONG) + sd(paruelo$LONG) * c(-2, -1, 0, 1, 2)) fit <- predict(paruelo.lm, newdata = newdata, interval = "confidence") #^2 fit <- cbind(newdata, fit) head(fit)
LAT LONG fit lwr upr 1 29.00000 93.5293 0.3063215 0.09947146 0.5131716 2 29.23364 93.5293 0.3096665 0.10635971 0.5129732 3 29.46727 93.5293 0.3130114 0.11322587 0.5127969 4 29.70091 93.5293 0.3163563 0.12006878 0.5126438 5 29.93455 93.5293 0.3197012 0.12688716 0.5125153 6 30.16818 93.5293 0.3230461 0.13367966 0.5124126
# calculated the partial observed values partial.obs <- expand.grid(LAT = paruelo$LAT, LONG = mean(paruelo$LONG) + sd(paruelo$LONG) * c(-2, -1, 0, 1, 2)) partial.obs <- cbind(partial.obs, fit = predict(paruelo.lm, newdata = partial.obs)) partial.obs$fit <- (partial.obs$fit + resid(paruelo.lm)) #^2 head(partial.obs)
LAT LONG fit 1 46.40 93.5293 0.5071849 2 47.32 93.5293 0.5243126 3 45.78 93.5293 0.6979391 4 43.95 93.5293 0.8168116 5 46.90 93.5293 0.4570809 6 38.87 93.5293 0.2065210
fit$lLONG <- factor(fit$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$lLONG <- factor(partial.obs$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) library(ggplot2) ggplot(fit, aes(y = fit, x = LAT)) + geom_point(data = partial.obs) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous(expression(Abundance ~ of ~ C3 ~ grasses ~ (sqrt(phantom(x))))) + scale_x_continuous(expression(Latitude ~ (degree * S))) + facet_grid(~lLONG, labeller = label_parsed) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank())
 Show emmeans code
Show emmeans codeparuelo.list = with(paruelo, list(LAT = seq(min(LAT), max(LAT), len = 100), LONG = mean(LONG) + sd(LONG) * c(-2, -1, 0, 1, 2))) paruelo.grid = ref_grid(paruelo.lm, ~LAT | LONG, at = paruelo.list, cov.reduce = function(x) x) newdata = confint(paruelo.grid) ## calculate the partial residuals partial.obs = ref_grid(paruelo.lm, ~LAT, cov.reduce = function(x) x, at = list(LONG = mean(paruelo$LONG) + sd(paruelo$LONG) * c(-2, -1, 0, 1, 2))) %>% summary %>% mutate(presid = prediction + as.vector(resid(paruelo.lm))) newdata$lLONG <- factor(newdata$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$lLONG <- factor(partial.obs$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) ggplot(newdata, aes(y = prediction, x = LAT)) + geom_line() + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), color = "grey", alpha = 0.3) + facet_grid(~lLONG, labeller = label_parsed) + scale_y_continuous(expression(Abundance ~ of ~ C3 ~ grasses ~ (sqrt(phantom(x))))) + scale_x_continuous(expression(Latitude ~ (degree * S))) + geom_point(data = partial.obs, aes(y = presid)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank())
 Show manual code
Show manual codenewdata = with(paruelo, expand.grid(LAT = seq(min(LAT), max(LAT), len = 100), LONG = mean(LONG) + sd(LONG) * c(-2, -1, 0, 1, 2))) Xmat = model.matrix(~scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = newdata) coefs = coef(paruelo.lm) fit = as.vector(coefs %*% t(Xmat)) se = sqrt(diag(Xmat %*% vcov(paruelo.lm) %*% t(Xmat))) q = qt(0.975, df = df.residual(paruelo.lm)) newdata = newdata %>% bind_cols(data.frame(fit = fit, lwr = fit - q * se, upr = fit + q * se)) ## partial residuals partial.obs <- with(paruelo, expand.grid(LAT = LAT, LONG = mean(LAT) + sd(LAT) * c(-2, -1, 0, 1, 2))) Xmat = model.matrix(~scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = partial.obs) presid = as.vector(coefs %*% t(Xmat)) partial.obs = partial.obs %>% bind_cols(data.frame(presid = presid + rep(resid(paruelo.lm), 5))) newdata$lLONG <- factor(newdata$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$lLONG <- factor(partial.obs$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) ggplot(newdata, aes(y = fit, x = LAT)) + geom_line() + geom_ribbon(aes(ymin = lwr, ymax = upr), color = "grey", alpha = 0.3) + facet_grid(~lLONG, labeller = label_parsed) + scale_y_continuous(expression(Abundance ~ of ~ C3 ~ grasses ~ (sqrt(phantom(x))))) + scale_x_continuous(expression(Latitude ~ (degree * S))) + geom_point(data = partial.obs, aes(y = presid)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank())

- Whilst this was not actually a spatial analysis, the predictors were of
a spatial nature. It might therefore be interesting to visualize the predictions as a heat
map projected onto lat/long space. We could even overlay this onto a map of North America
so as to visualize the spatial patterns in C3 grass abundances.
Show predict code
## Lets start by getting the base map of USA library(mapdata) library(maps) library(sf) ## Get a map of the USA usa = map("usa", plot = FALSE) ## convert it to standard features usa = st_as_sf(usa) plot(usa)

newdata <- with(paruelo, expand.grid(LAT = seq(min(LAT), max(LAT), len = 100), LONG = seq(min(LONG), max(LONG), len = 100))) ## The above grid is defined by the maximum bounding ## latitude/longitude bounding box. However, the sampling ## design was not a perfect rectangle and therefore this ## bounding box would involve predictions outside the spatial ## sampling domain. We should probably restrict the grid to a ## polygon defined by a convex hull around the points. We can ## do this either by cropping/masking out the grid we just ## made or generate a regular grid from within the convex ## hull. paruelo.sf = paruelo %>% mutate(LONG = LONG * -1) %>% st_as_sf(coords = c("LONG", "LAT")) newdata = paruelo.sf %>% st_union %>% st_convex_hull %>% st_set_crs(st_crs(usa)) ggplot() + geom_sf(data = usa) + geom_sf(data = newdata, fill = NA)

## We can see that the prediction grid protrudes outside of ## the USA, so we might want to crop it so that it is ## contained in the USA polygon newdata = newdata %>% st_set_crs(st_crs(usa)) %>% st_intersection(st_buffer(usa, 0)) #st_buffer needed as some usa polygons intersect ggplot() + geom_sf(data = usa) + geom_sf(data = newdata)

newdata = newdata %>% st_set_crs(NA) %>% st_sample(size = 10000, type = "regular", exact = TRUE) %>% st_set_crs(st_crs(usa)) %>% st_coordinates %>% as.data.frame %>% dplyr::rename(LAT = Y, LONG = X) fit <- predict(paruelo.lm, newdata = newdata, interval = "confidence") fit <- cbind(newdata, fit) head(fit)
LONG LAT fit lwr upr 1 -98.38595 29.15257 5.657915 2.183853 9.131978 2 -98.18389 29.15257 5.652283 2.181692 9.122874 3 -97.98184 29.15257 5.646651 2.179531 9.113771 4 -97.77979 29.15257 5.641019 2.177370 9.104668 5 -97.57774 29.15257 5.635387 2.175210 9.095565 6 -97.37569 29.15257 5.629755 2.173049 9.086462
## Note, the Longitude are positive (and thus Easterly), we ## need to multiply them by -1 ggplot() + geom_sf(data = usa) + geom_tile(data = fit, aes(y = LAT, x = LONG, fill = fit)) + scale_fill_gradientn(colors = heat.colors(12)) + theme_bw()

We obviously cannot easily incorporate all 6 predictors into the one model, because of the collinearity problem. Paruelo and Lauenroth (1996) separated the predictors into two groups for their analyses. One group included LAT and LONG and the other included MAP, MAT, JJAMAP and DJFMAP. We will focus on the relationship between the square root relative abundance of C3 plants and latitude and longitude. This relationship will investigate the geographic pattern in abundance of C3 plants.
Note the figures above are on a square-root scale AND the some trends and confidence intervals extend into negative square-root C3 abundances. Clearly this is not logical and is an artifact of applying a square-root transformation to normalize the data when there were numerous response values close to zero.
If we were to back transform these relationships, we would be confronted with a parabola-like relationship. This is obviously an artefact of the fitting a model to root transformed data and is highly unlikely to reflect any genuine ecological trends. To illustrate, lets repeat the above and apply the back transformations.
newdata <- expand.grid(LAT = seq(min(paruelo$LAT), max(paruelo$LAT), len = 100), LONG = mean(paruelo$LONG) + sd(paruelo$LONG) * c(-2, -1, 0, 1, 2)) fit <- predict(paruelo.lm, newdata = newdata, interval = "confidence")^2 fit <- cbind(newdata, fit) head(fit)
LAT LONG fit lwr upr 1 29.00000 93.5293 0.09383288 0.009894572 0.2633451 2 29.23364 93.5293 0.09589331 0.011312387 0.2631415 3 29.46727 93.5293 0.09797612 0.012820099 0.2629606 4 29.70091 93.5293 0.10008130 0.014416512 0.2628037 5 29.93455 93.5293 0.10220886 0.016100351 0.2626719 6 30.16818 93.5293 0.10435880 0.017870251 0.2625667
# calculated the partial observed values partial.obs <- expand.grid(LAT = paruelo$LAT, LONG = mean(paruelo$LONG) + sd(paruelo$LONG) * c(-2, -1, 0, 1, 2)) partial.obs <- cbind(partial.obs, fit = predict(paruelo.lm, newdata = partial.obs)) partial.obs$fit <- (partial.obs$fit + resid(paruelo.lm))^2 head(partial.obs)
LAT LONG fit 1 46.40 93.5293 0.25723651 2 47.32 93.5293 0.27490373 3 45.78 93.5293 0.48711906 4 43.95 93.5293 0.66718116 5 46.90 93.5293 0.20892295 6 38.87 93.5293 0.04265093
fit$lLONG <- factor(fit$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$lLONG <- factor(partial.obs$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) library(ggplot2) ggplot(fit, aes(y = fit, x = LAT)) + geom_point(data = partial.obs) + geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2, color = NA) + geom_line() + scale_y_continuous(expression(Abundance ~ of ~ C3 ~ grasses)) + scale_x_continuous(expression(Latitude ~ (degree * S))) + facet_grid(~lLONG, labeller = label_parsed) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank())
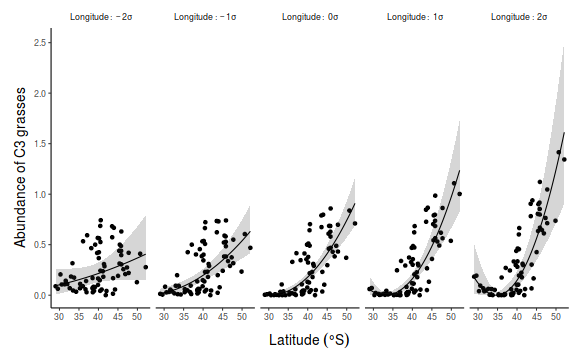
paruelo.list = with(paruelo, list(LAT = seq(min(LAT), max(LAT), len = 100), LONG = mean(LONG) + sd(LONG) * c(-2, -1, 0, 1, 2))) paruelo.grid = ref_grid(paruelo.lm, ~LAT | LONG, at = paruelo.list, cov.reduce = function(x) x) newdata = confint(paruelo.grid) %>% mutate_at(vars(prediction, lower.CL, upper.CL), function(x) x^2) ## calculate the partial residuals partial.obs = ref_grid(paruelo.lm, ~LAT, cov.reduce = function(x) x, at = list(LONG = mean(paruelo$LONG) + sd(paruelo$LONG) * c(-2, -1, 0, 1, 2))) %>% summary %>% mutate(presid = (prediction + as.vector(resid(paruelo.lm)))^2) newdata$lLONG <- factor(newdata$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$lLONG <- factor(partial.obs$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) ggplot(newdata, aes(y = prediction, x = LAT)) + geom_line() + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), color = "grey", alpha = 0.3) + facet_grid(~lLONG, labeller = label_parsed) + scale_y_continuous(expression(Abundance ~ of ~ C3 ~ grasses)) + scale_x_continuous(expression(Latitude ~ (degree * S))) + geom_point(data = partial.obs, aes(y = presid)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank())
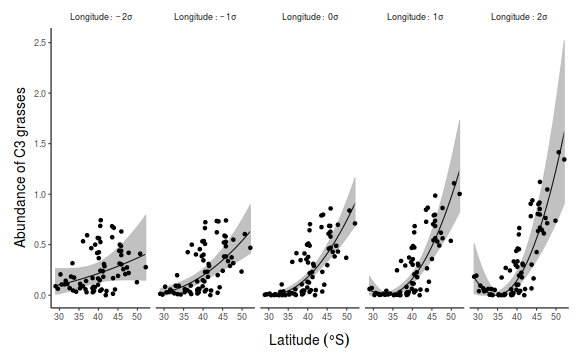
newdata = with(paruelo, expand.grid(LAT = seq(min(LAT), max(LAT), len = 100), LONG = mean(LONG) + sd(LONG) * c(-2, -1, 0, 1, 2))) Xmat = model.matrix(~scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = newdata) coefs = coef(paruelo.lm) fit = as.vector(coefs %*% t(Xmat)) se = sqrt(diag(Xmat %*% vcov(paruelo.lm) %*% t(Xmat))) q = qt(0.975, df = df.residual(paruelo.lm)) newdata = newdata %>% bind_cols(data.frame(fit = fit^2, lwr = (fit - q * se)^2, upr = (fit + q * se)^2)) ## partial residuals partial.obs <- with(paruelo, expand.grid(LAT = LAT, LONG = mean(LAT) + sd(LAT) * c(-2, -1, 0, 1, 2))) Xmat = model.matrix(~scale(LAT, scale = FALSE) * scale(LONG, scale = FALSE), data = partial.obs) presid = as.vector(coefs %*% t(Xmat)) partial.obs = partial.obs %>% bind_cols(data.frame(presid = (presid + rep(resid(paruelo.lm), 5))^2)) newdata$lLONG <- factor(newdata$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) partial.obs$lLONG <- factor(partial.obs$LONG, labels = paste("Longitude:~", c(-2, -1, 0, 1, 2), "*sigma")) ggplot(newdata, aes(y = fit, x = LAT)) + geom_line() + geom_ribbon(aes(ymin = lwr, ymax = upr), color = "grey", alpha = 0.3) + facet_grid(~lLONG, labeller = label_parsed) + scale_y_continuous(expression(Abundance ~ of ~ C3 ~ grasses)) + scale_x_continuous(expression(Latitude ~ (degree * S))) + geom_point(data = partial.obs, aes(y = presid)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines"), strip.background = element_blank())
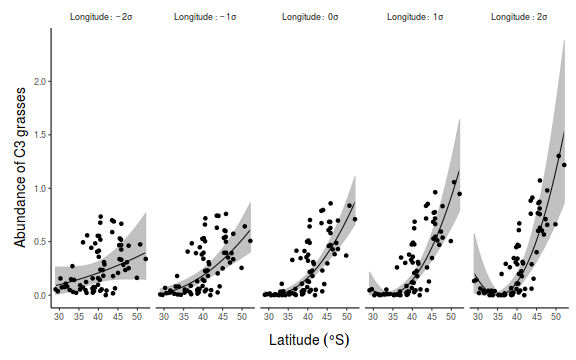
Notice the hook in the predictions associated with low Latitude. This is an artifact of the back-transformation.
Arguably, it would have been more appropriate to fit a generalized linear model with a binomial distribution. We will therefore return to this example in Tutorial 10.5a.
Multiple Linear Regression
Loyn (1987) modeled the abundance of forest birds with six predictor variables (patch area, distance to nearest patch, distance to nearest larger patch, grazing intensity, altitude and years since the patch had been isolated).
Download Loyn data set| Format of loyn.csv data file | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
loyn <- read.table("../downloads/data/loyn.csv", header = T, sep = ",", strip.white = T) head(loyn)
ABUND AREA YR.ISOL DIST LDIST GRAZE ALT 1 5.3 0.1 1968 39 39 2 160 2 2.0 0.5 1920 234 234 5 60 3 1.5 0.5 1900 104 311 5 140 4 17.1 1.0 1966 66 66 3 160 5 13.8 1.0 1918 246 246 5 140 6 14.1 1.0 1965 234 285 3 130
- In the table below, list the assumptions of multiple linear regression along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
Assumption Diagnostic/Risk Minimization I. II. III. IV. V. - Construct a
scatterplot matrix
to investigate these assumptions(HINT)
Show scatterplotMatrix (car) code
library(car) scatterplotMatrix(~ABUND + DIST + LDIST + AREA + GRAZE + ALT + YR.ISOL, data = loyn, diagonal = list(method = "boxplot"))
 Show splom (lattice) code
Show splom (lattice) codelibrary(lattice) splom.lat <- splom(loyn, type = c("p", "r")) print(splom.lat)
 Show ggpairs (GGally) code
Show ggpairs (GGally) codelibrary(GGally) ggpairs(loyn, lower = list(continuous = "smooth"), diag = list(continuous = "density"), axisLabels = "none")

- Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?
- Try applying a temporary log10 transformation to the skewed variables(HINT).
Show scatterplotMatrix (car) code
library(car) scatterplotMatrix(~ABUND + log10(DIST) + log10(LDIST) + log10(AREA) + GRAZE + ALT + YR.ISOL, data = loyn, diagonal = list(margin = "boxplot"))
 Show ggpairs (GGally) codeDoes this improve some of these specific assumptions (y or n)?
Show ggpairs (GGally) codeDoes this improve some of these specific assumptions (y or n)?library(GGally) ggpairs(with(loyn, data.frame(logDIST = log10(DIST), logLDIST = log(LDIST), logAREA = log10(AREA), GRAZE, ALT, YR.ISOL)), lower = list(continuous = "smooth"), diag = list(continuous = "density"), axisLabels = "none")

- Is there any evidence that the assumption of Collinearity is likely to be violated (y or n)?
Show code
loyn.lm <- lm(ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) + GRAZE + ALT + YR.ISOL, data = loyn) vif(loyn.lm)
log10(DIST) log10(LDIST) log10(AREA) GRAZE ALT YR.ISOL 1.654553 2.009749 1.911514 2.524814 1.467937 1.8047691/vif(loyn.lm)
log10(DIST) log10(LDIST) log10(AREA) GRAZE ALT YR.ISOL 0.6043930 0.4975746 0.5231454 0.3960688 0.6812282 0.5540876
Predictor VIF Tolerance log10(DIST) log10(LDIST) log10(AREA) GRAZE ALT YR.ISOL - Collinearity typically occurs when one or more of the predictor variables are correlated, therefore this assumption can also be examined by calculating the pairwise correlation coefficients between all the predictor variables (use transformed versions for those that required it) (
HINT).
Show codeNone of the predictor variables are overly correlated to any of the other predictor variables.
cor(loyn.lm$model[, 2:7])
log10(DIST) log10(LDIST) log10(AREA) GRAZE ALT YR.ISOL log10(DIST) 1.00000000 0.60386637 0.3021666 -0.14263922 -0.2190070 -0.01957223 log10(LDIST) 0.60386637 1.00000000 0.3824795 -0.03399082 -0.2740438 -0.16111611 log10(AREA) 0.30216662 0.38247952 1.0000000 -0.55908864 0.2751428 0.27841452 GRAZE -0.14263922 -0.03399082 -0.5590886 1.00000000 -0.4071671 -0.63556710 ALT -0.21900701 -0.27404380 0.2751428 -0.40716705 1.0000000 0.23271541 YR.ISOL -0.01957223 -0.16111611 0.2784145 -0.63556710 0.2327154 1.00000000
- Focussing on the assumptions of Normality, Homogeneity of Variance and Linearity, is there evidence of violations of these assumptions (y or n)?
- Construct a predictive model for relating habitat variables to forest bird abundances
- Determine which are the most important (influential) predictor variables of forest bird abundances
-
Fit an additive linear model
relating ABUND to each of the predictor variables, but no interactions (
HINT)
Show code
loyn.lm <- lm(ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) + GRAZE + ALT + YR.ISOL, data = loyn)
- Examine the diagnostic plots (HINT) specially the residual plot to confirm no further evidence of violations of the analysis assumptions
Show base code
# setup a 2x6 plotting device with small margins par(mfrow = c(2, 3), oma = c(0, 0, 2, 0)) plot(loyn.lm, ask = F, which = 1:6)

influence.measures(loyn.lm)
Influence measures of lm(formula = ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) + GRAZE + ALT + YR.ISOL, data = loyn) : dfb.1_ dfb.l10.D dfb.l10.L dfb.l10.A dfb.GRAZ dfb.ALT dfb.YR.I dffit cov.r cook.d 1 -0.024547 0.08371 -0.022664 0.325348 0.219000 -0.005547 0.008468 -0.4206 1.395 2.55e-02 2 -0.017509 -0.01656 0.020997 0.012653 0.003658 0.037247 0.016013 -0.0657 1.319 6.29e-04 3 -0.058912 0.01045 -0.016321 0.048309 0.012241 -0.021952 0.060904 -0.1103 1.288 1.77e-03 4 -0.024649 -0.01083 -0.015504 -0.047360 -0.005965 0.010247 0.028327 0.0998 1.217 1.45e-03 5 0.064514 0.17236 -0.075678 -0.091673 0.105181 0.101385 -0.078406 0.3575 1.036 1.81e-02 6 -0.013955 0.01154 0.003907 -0.027075 -0.003667 0.000920 0.014184 0.0385 1.243 2.16e-04 7 0.152729 -0.14223 0.018225 0.056318 -0.149535 0.022629 -0.148486 -0.2837 1.250 1.16e-02 8 -0.012535 0.00936 -0.059652 0.050580 -0.001515 0.058081 0.012466 -0.1520 1.289 3.36e-03 9 0.240434 -0.10307 0.040989 0.142365 -0.165009 -0.019501 -0.243854 -0.4029 0.937 2.27e-02 10 -0.049652 -0.03654 -0.001350 0.035981 -0.001217 -0.021708 0.054131 -0.1064 1.286 1.65e-03 11 0.326311 -0.29680 0.393485 -0.464543 -0.259851 0.555537 -0.347149 0.9263 0.653 1.13e-01 12 -0.318813 -0.04143 0.184910 -0.047393 0.001434 -0.058520 0.324669 -0.4586 1.179 3.00e-02 13 -0.003880 -0.00858 -0.003634 -0.013295 -0.006816 0.013654 0.004853 0.0364 1.302 1.93e-04 14 0.049590 -0.19049 -0.118128 0.391650 0.193189 -0.285935 -0.033841 -0.5334 1.236 4.06e-02 15 0.028372 0.01892 -0.019252 0.001533 0.002733 -0.003094 -0.029406 0.0490 1.295 3.50e-04 16 -0.112157 0.03131 -0.058961 0.040297 -0.017552 -0.062221 0.119657 -0.2278 1.199 7.50e-03 17 0.089920 -0.36895 -0.418556 0.197950 -0.137942 -0.554335 -0.016929 0.9038 0.798 1.10e-01 18 0.003210 0.44969 0.471153 -0.189555 0.055517 0.413749 -0.081604 -1.0674 0.459 1.43e-01 19 -0.014516 -0.05622 -0.077388 0.014877 0.026729 0.051520 0.021493 0.2163 1.162 6.75e-03 20 0.031138 0.01561 -0.029390 -0.019603 -0.059824 -0.066354 -0.026445 0.0950 1.281 1.31e-03 21 -0.074573 0.03497 0.084655 -0.115333 0.004721 0.153777 0.066229 0.1998 1.318 5.80e-03 22 0.012462 0.62313 -0.547520 0.034210 -0.102778 0.004117 -0.020621 -0.7615 1.323 8.21e-02 23 0.007417 0.07767 0.112948 -0.066606 0.000558 0.110277 -0.024123 -0.2259 1.218 7.38e-03 24 0.057330 0.06179 -0.042947 -0.103211 -0.203842 -0.153868 -0.046055 0.2864 1.253 1.18e-02 25 0.399742 -0.06158 -0.055316 -0.020120 -0.228704 0.012557 -0.400107 0.4310 1.320 2.67e-02 26 -0.036316 -0.02478 0.062377 -0.032586 0.009891 0.023836 0.035302 0.0810 1.209 9.54e-04 27 0.062196 -0.01369 -0.045659 0.029139 -0.023443 -0.004247 -0.061136 -0.1034 1.178 1.55e-03 28 0.022345 -0.01170 0.005156 -0.004665 -0.032184 -0.032509 -0.020565 -0.0462 1.322 3.11e-04 29 -0.048454 0.02411 -0.016234 0.017630 0.047216 -0.006470 0.048550 0.0678 1.284 6.70e-04 30 0.020424 0.00550 0.013709 0.018552 0.021831 -0.019583 -0.022322 0.0809 1.272 9.54e-04 31 0.181882 -0.18332 0.070644 -0.044548 -0.080909 0.204938 -0.188993 -0.4816 0.632 3.08e-02 32 -0.004554 -0.00646 -0.010581 0.012558 0.011367 0.000130 0.005339 0.0235 1.380 8.04e-05 33 -0.192246 0.07100 -0.214312 0.246055 0.262466 -0.178104 0.205265 0.4545 0.968 2.89e-02 34 -0.167748 0.08351 -0.072012 0.100394 0.263665 0.204739 0.156632 0.3493 1.149 1.75e-02 35 0.056797 -0.06516 0.082675 0.005839 0.006404 -0.128022 -0.056773 -0.2959 0.929 1.23e-02 36 -0.136228 -0.06411 0.004602 0.101551 0.082178 -0.132967 0.148678 0.2943 0.930 1.22e-02 37 0.004153 -0.01116 -0.045478 -0.053435 -0.081659 0.014926 0.001372 -0.1651 1.254 3.96e-03 38 -0.010846 -0.04066 0.048479 -0.013496 -0.004557 0.016275 0.010883 0.0559 1.679 4.56e-04 39 -0.222802 0.01356 0.109160 0.039879 0.210745 0.089951 0.214317 0.2799 1.260 1.13e-02 40 -0.005977 0.01113 -0.036499 -0.056239 -0.058831 0.032006 0.008643 -0.1378 1.287 2.76e-03 41 -0.031032 -0.08019 0.031978 0.020113 0.089394 0.033669 0.030566 -0.1590 1.221 3.67e-03 42 -0.029798 0.03356 -0.007763 0.018255 0.027276 -0.002476 0.028465 0.0597 1.236 5.19e-04 43 0.001060 -0.00833 0.008234 -0.000729 0.011017 -0.007667 -0.001249 -0.0327 1.228 1.56e-04 44 0.004393 -0.00930 0.000714 0.002619 -0.009448 -0.010691 -0.003254 0.0161 1.376 3.79e-05 45 0.011664 0.03240 -0.064340 0.046954 -0.013554 -0.053380 -0.008156 0.0934 1.260 1.27e-03 46 -0.044055 0.00853 -0.126785 0.175238 0.125507 0.057840 0.045178 0.2630 1.157 9.95e-03 47 0.348086 -0.09628 0.068676 0.328440 -0.113019 -0.256880 -0.347655 0.7168 0.485 6.55e-02 48 -0.139098 0.50451 0.055716 -0.138456 -0.085820 0.270712 0.103904 0.7515 0.885 7.74e-02 49 0.000830 0.00124 0.009247 -0.002171 -0.015170 -0.005737 -0.000635 0.0297 1.246 1.28e-04 50 0.010389 0.02638 -0.015605 0.006676 -0.022689 -0.000897 -0.010726 0.0536 1.242 4.18e-04 51 -0.048345 -0.13467 0.071349 0.066280 0.022910 0.002208 0.053729 0.1778 1.335 4.60e-03 52 -0.019314 0.04851 -0.061717 -0.025118 0.088505 0.129007 0.012520 -0.1989 1.421 5.75e-03 53 -0.000455 -0.00517 -0.030151 -0.009949 0.025032 -0.004643 0.001860 -0.0817 1.251 9.72e-04 54 0.032378 -0.00621 -0.010783 0.019668 -0.025119 -0.000179 -0.031927 0.0506 1.315 3.73e-04 55 0.072633 -0.00990 -0.045849 -0.458184 -0.072288 -0.111714 -0.060767 -0.7173 0.853 7.03e-02 56 -0.524582 -0.31857 0.429361 -0.754208 0.024705 -0.528460 0.569683 -1.3723 1.007 2.54e-01 hat inf 1 0.2374 2 0.1279 3 0.1150 4 0.0690 5 0.0849 6 0.0734 7 0.1399 8 0.1247 9 0.0748 10 0.1132 11 0.1413 12 0.1620 13 0.1142 14 0.2036 15 0.1105 16 0.0998 17 0.1704 18 0.1268 * 19 0.0804 20 0.1078 21 0.1513 22 0.2888 23 0.1079 24 0.1419 25 0.2095 26 0.0591 27 0.0487 28 0.1281 29 0.1053 30 0.0998 31 0.0472 32 0.1630 33 0.0962 34 0.1183 35 0.0452 36 0.0449 37 0.1085 38 0.3127 * 39 0.1435 40 0.1204 41 0.0888 42 0.0714 43 0.0611 44 0.1604 45 0.0943 46 0.0936 47 0.0693 * 48 0.1550 49 0.0746 50 0.0744 51 0.1561 52 0.2052 53 0.0862 54 0.1240 55 0.1384 56 0.3297 *Show autoplot codeautoplot(loyn.lm, which = 1:6)

influence.measures(loyn.lm)
Influence measures of lm(formula = ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) + GRAZE + ALT + YR.ISOL, data = loyn) : dfb.1_ dfb.l10.D dfb.l10.L dfb.l10.A dfb.GRAZ dfb.ALT dfb.YR.I dffit cov.r cook.d 1 -0.024547 0.08371 -0.022664 0.325348 0.219000 -0.005547 0.008468 -0.4206 1.395 2.55e-02 2 -0.017509 -0.01656 0.020997 0.012653 0.003658 0.037247 0.016013 -0.0657 1.319 6.29e-04 3 -0.058912 0.01045 -0.016321 0.048309 0.012241 -0.021952 0.060904 -0.1103 1.288 1.77e-03 4 -0.024649 -0.01083 -0.015504 -0.047360 -0.005965 0.010247 0.028327 0.0998 1.217 1.45e-03 5 0.064514 0.17236 -0.075678 -0.091673 0.105181 0.101385 -0.078406 0.3575 1.036 1.81e-02 6 -0.013955 0.01154 0.003907 -0.027075 -0.003667 0.000920 0.014184 0.0385 1.243 2.16e-04 7 0.152729 -0.14223 0.018225 0.056318 -0.149535 0.022629 -0.148486 -0.2837 1.250 1.16e-02 8 -0.012535 0.00936 -0.059652 0.050580 -0.001515 0.058081 0.012466 -0.1520 1.289 3.36e-03 9 0.240434 -0.10307 0.040989 0.142365 -0.165009 -0.019501 -0.243854 -0.4029 0.937 2.27e-02 10 -0.049652 -0.03654 -0.001350 0.035981 -0.001217 -0.021708 0.054131 -0.1064 1.286 1.65e-03 11 0.326311 -0.29680 0.393485 -0.464543 -0.259851 0.555537 -0.347149 0.9263 0.653 1.13e-01 12 -0.318813 -0.04143 0.184910 -0.047393 0.001434 -0.058520 0.324669 -0.4586 1.179 3.00e-02 13 -0.003880 -0.00858 -0.003634 -0.013295 -0.006816 0.013654 0.004853 0.0364 1.302 1.93e-04 14 0.049590 -0.19049 -0.118128 0.391650 0.193189 -0.285935 -0.033841 -0.5334 1.236 4.06e-02 15 0.028372 0.01892 -0.019252 0.001533 0.002733 -0.003094 -0.029406 0.0490 1.295 3.50e-04 16 -0.112157 0.03131 -0.058961 0.040297 -0.017552 -0.062221 0.119657 -0.2278 1.199 7.50e-03 17 0.089920 -0.36895 -0.418556 0.197950 -0.137942 -0.554335 -0.016929 0.9038 0.798 1.10e-01 18 0.003210 0.44969 0.471153 -0.189555 0.055517 0.413749 -0.081604 -1.0674 0.459 1.43e-01 19 -0.014516 -0.05622 -0.077388 0.014877 0.026729 0.051520 0.021493 0.2163 1.162 6.75e-03 20 0.031138 0.01561 -0.029390 -0.019603 -0.059824 -0.066354 -0.026445 0.0950 1.281 1.31e-03 21 -0.074573 0.03497 0.084655 -0.115333 0.004721 0.153777 0.066229 0.1998 1.318 5.80e-03 22 0.012462 0.62313 -0.547520 0.034210 -0.102778 0.004117 -0.020621 -0.7615 1.323 8.21e-02 23 0.007417 0.07767 0.112948 -0.066606 0.000558 0.110277 -0.024123 -0.2259 1.218 7.38e-03 24 0.057330 0.06179 -0.042947 -0.103211 -0.203842 -0.153868 -0.046055 0.2864 1.253 1.18e-02 25 0.399742 -0.06158 -0.055316 -0.020120 -0.228704 0.012557 -0.400107 0.4310 1.320 2.67e-02 26 -0.036316 -0.02478 0.062377 -0.032586 0.009891 0.023836 0.035302 0.0810 1.209 9.54e-04 27 0.062196 -0.01369 -0.045659 0.029139 -0.023443 -0.004247 -0.061136 -0.1034 1.178 1.55e-03 28 0.022345 -0.01170 0.005156 -0.004665 -0.032184 -0.032509 -0.020565 -0.0462 1.322 3.11e-04 29 -0.048454 0.02411 -0.016234 0.017630 0.047216 -0.006470 0.048550 0.0678 1.284 6.70e-04 30 0.020424 0.00550 0.013709 0.018552 0.021831 -0.019583 -0.022322 0.0809 1.272 9.54e-04 31 0.181882 -0.18332 0.070644 -0.044548 -0.080909 0.204938 -0.188993 -0.4816 0.632 3.08e-02 32 -0.004554 -0.00646 -0.010581 0.012558 0.011367 0.000130 0.005339 0.0235 1.380 8.04e-05 33 -0.192246 0.07100 -0.214312 0.246055 0.262466 -0.178104 0.205265 0.4545 0.968 2.89e-02 34 -0.167748 0.08351 -0.072012 0.100394 0.263665 0.204739 0.156632 0.3493 1.149 1.75e-02 35 0.056797 -0.06516 0.082675 0.005839 0.006404 -0.128022 -0.056773 -0.2959 0.929 1.23e-02 36 -0.136228 -0.06411 0.004602 0.101551 0.082178 -0.132967 0.148678 0.2943 0.930 1.22e-02 37 0.004153 -0.01116 -0.045478 -0.053435 -0.081659 0.014926 0.001372 -0.1651 1.254 3.96e-03 38 -0.010846 -0.04066 0.048479 -0.013496 -0.004557 0.016275 0.010883 0.0559 1.679 4.56e-04 39 -0.222802 0.01356 0.109160 0.039879 0.210745 0.089951 0.214317 0.2799 1.260 1.13e-02 40 -0.005977 0.01113 -0.036499 -0.056239 -0.058831 0.032006 0.008643 -0.1378 1.287 2.76e-03 41 -0.031032 -0.08019 0.031978 0.020113 0.089394 0.033669 0.030566 -0.1590 1.221 3.67e-03 42 -0.029798 0.03356 -0.007763 0.018255 0.027276 -0.002476 0.028465 0.0597 1.236 5.19e-04 43 0.001060 -0.00833 0.008234 -0.000729 0.011017 -0.007667 -0.001249 -0.0327 1.228 1.56e-04 44 0.004393 -0.00930 0.000714 0.002619 -0.009448 -0.010691 -0.003254 0.0161 1.376 3.79e-05 45 0.011664 0.03240 -0.064340 0.046954 -0.013554 -0.053380 -0.008156 0.0934 1.260 1.27e-03 46 -0.044055 0.00853 -0.126785 0.175238 0.125507 0.057840 0.045178 0.2630 1.157 9.95e-03 47 0.348086 -0.09628 0.068676 0.328440 -0.113019 -0.256880 -0.347655 0.7168 0.485 6.55e-02 48 -0.139098 0.50451 0.055716 -0.138456 -0.085820 0.270712 0.103904 0.7515 0.885 7.74e-02 49 0.000830 0.00124 0.009247 -0.002171 -0.015170 -0.005737 -0.000635 0.0297 1.246 1.28e-04 50 0.010389 0.02638 -0.015605 0.006676 -0.022689 -0.000897 -0.010726 0.0536 1.242 4.18e-04 51 -0.048345 -0.13467 0.071349 0.066280 0.022910 0.002208 0.053729 0.1778 1.335 4.60e-03 52 -0.019314 0.04851 -0.061717 -0.025118 0.088505 0.129007 0.012520 -0.1989 1.421 5.75e-03 53 -0.000455 -0.00517 -0.030151 -0.009949 0.025032 -0.004643 0.001860 -0.0817 1.251 9.72e-04 54 0.032378 -0.00621 -0.010783 0.019668 -0.025119 -0.000179 -0.031927 0.0506 1.315 3.73e-04 55 0.072633 -0.00990 -0.045849 -0.458184 -0.072288 -0.111714 -0.060767 -0.7173 0.853 7.03e-02 56 -0.524582 -0.31857 0.429361 -0.754208 0.024705 -0.528460 0.569683 -1.3723 1.007 2.54e-01 hat inf 1 0.2374 2 0.1279 3 0.1150 4 0.0690 5 0.0849 6 0.0734 7 0.1399 8 0.1247 9 0.0748 10 0.1132 11 0.1413 12 0.1620 13 0.1142 14 0.2036 15 0.1105 16 0.0998 17 0.1704 18 0.1268 * 19 0.0804 20 0.1078 21 0.1513 22 0.2888 23 0.1079 24 0.1419 25 0.2095 26 0.0591 27 0.0487 28 0.1281 29 0.1053 30 0.0998 31 0.0472 32 0.1630 33 0.0962 34 0.1183 35 0.0452 36 0.0449 37 0.1085 38 0.3127 * 39 0.1435 40 0.1204 41 0.0888 42 0.0714 43 0.0611 44 0.1604 45 0.0943 46 0.0936 47 0.0693 * 48 0.1550 49 0.0746 50 0.0744 51 0.1561 52 0.2052 53 0.0862 54 0.1240 55 0.1384 56 0.3297 * - On initial examination of the fitted model summary, which of the predictor variables might
you consider important? (this can initially be determined by exploring which of the effects are significant?)
Show codesummary(loyn.lm)
Call: lm(formula = ABUND ~ log10(DIST) + log10(LDIST) + log10(AREA) + GRAZE + ALT + YR.ISOL, data = loyn) Residuals: Min 1Q Median 3Q Max -15.6506 -2.9390 0.5289 2.5353 15.2842 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -125.69725 91.69228 -1.371 0.1767 log10(DIST) -0.90696 2.67572 -0.339 0.7361 log10(LDIST) -0.64842 2.12270 -0.305 0.7613 log10(AREA) 7.47023 1.46489 5.099 5.49e-06 *** GRAZE -1.66774 0.92993 -1.793 0.0791 . ALT 0.01951 0.02396 0.814 0.4195 YR.ISOL 0.07387 0.04520 1.634 0.1086 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6.384 on 49 degrees of freedom Multiple R-squared: 0.6849, Adjusted R-squared: 0.6464 F-statistic: 17.75 on 6 and 49 DF, p-value: 8.443e-11confint(loyn.lm)
2.5 % 97.5 % (Intercept) -309.95977340 58.56528176 log10(DIST) -6.28402047 4.47010711 log10(LDIST) -4.91414111 3.61730123 log10(AREA) 4.52641155 10.41404091 GRAZE -3.53649663 0.20101975 ALT -0.02863924 0.06765562 YR.ISOL -0.01697045 0.16471247
tidy(loyn.lm)
# A tibble: 7 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) -126. 91.7 -1.37 0.177 2 log10(DIST) -0.907 2.68 -0.339 0.736 3 log10(LDIST) -0.648 2.12 -0.305 0.761 4 log10(AREA) 7.47 1.46 5.10 0.00000549 5 GRAZE -1.67 0.930 -1.79 0.0791 6 ALT 0.0195 0.0240 0.814 0.419 7 YR.ISOL 0.0739 0.0452 1.63 0.109
Coefficient Estimate t-value P-value Intercept log10(DIST) log10(LDIST) log10(AREA) GRAZE ALT YR.ISOL
Clearly, not all of the predictor variables have significant partial effects on the abundance of forest birds. In developing a predictive model for relating forest bird abundances to a range of habitat characteristics, not all of the measured variables are useful. Likewise, the measured variables are not likely to be equally influential in determining the abundance of forest birds.
- Examine the diagnostic plots (HINT) specially the residual plot to confirm no further evidence of violations of the analysis assumptions
- We would now like to be able to find the
'best' regression model whilst remaining mindful of the criticisms against such an approach..
Calculate the adjusted R2 (HINT),
generic AIC (HINT) and
generic BIC (HINT) for the full regression containing all six predictor variables.
Show code
summary(loyn.lm)$adj.r.squared
[1] 0.6463567
AIC(loyn.lm)
[1] 375.0638
AIC(loyn.lm, k = log(nrow(loyn)))
[1] 391.2666
library(MuMIn) AICc(loyn.lm)
[1] 378.1276
Model Adj. r2 AIC BIC Full Q2-5. Compare all possible models and select the 'best' (most parsimonious) model based on AIC and investigate the importance of each of the predictor variables using model averaging (HINT).Show codelibrary(MuMIn) # for more recent versions of MuMIn, it is necessary that the model be fitted with na.action=na.fail loyn.lm <- update(loyn.lm, na.action = na.fail) loyn.av <- model.avg(get.models(dredge(loyn.lm, rank = "AIC"), subset = delta <= 100)) summary(loyn.av)
Call: model.avg(object = get.models(dredge(loyn.lm, rank = "AIC"), subset = delta <= 100)) Component model call: lm(formula = ABUND ~ <64 unique rhs>, data = loyn, na.action = na.fail) Component models: df logLik AIC delta weight 236 5 -180.55 371.11 0.00 0.13 1236 6 -179.76 371.52 0.41 0.10 2356 6 -180.04 372.07 0.96 0.08 2346 6 -180.07 372.14 1.04 0.08 23 4 -182.26 372.51 1.40 0.06 235 5 -181.35 372.69 1.59 0.06 136 5 -181.43 372.86 1.75 0.05 123 5 -181.58 373.15 2.05 0.05 234 5 -181.58 373.16 2.06 0.05 12346 7 -179.59 373.17 2.06 0.05 12356 7 -179.60 373.19 2.09 0.04 23456 7 -179.91 373.82 2.71 0.03 36 4 -182.99 373.99 2.88 0.03 1235 6 -181.09 374.19 3.08 0.03 2345 6 -181.23 374.45 3.34 0.02 1234 6 -181.24 374.48 3.37 0.02 1356 6 -181.32 374.63 3.52 0.02 356 5 -182.36 374.72 3.61 0.02 1346 6 -181.38 374.76 3.65 0.02 123456 8 -179.53 375.06 3.95 0.02 346 5 -182.64 375.28 4.17 0.02 12345 7 -181.02 376.04 4.93 0.01 13456 7 -181.31 376.62 5.51 0.01 3456 6 -182.32 376.64 5.54 0.01 13 4 -187.34 382.68 11.57 0.00 135 5 -186.55 383.10 11.99 0.00 35 4 -187.61 383.23 12.12 0.00 134 5 -187.23 384.45 13.34 0.00 1345 6 -186.54 385.07 13.97 0.00 345 5 -187.61 385.23 14.12 0.00 3 3 -189.66 385.32 14.21 0.00 34 4 -189.01 386.02 14.91 0.00 2 3 -194.31 394.63 23.52 0.00 1256 6 -191.46 394.91 23.80 0.00 125 5 -192.51 395.01 23.91 0.00 12 4 -193.57 395.15 24.04 0.00 25 4 -193.84 395.68 24.57 0.00 26 4 -193.89 395.77 24.66 0.00 126 5 -193.09 396.17 25.07 0.00 256 5 -193.11 396.22 25.11 0.00 24 4 -194.27 396.54 25.43 0.00 124 5 -193.31 396.63 25.52 0.00 12456 7 -191.45 396.90 25.80 0.00 1245 6 -192.50 397.00 25.89 0.00 1246 6 -192.68 397.36 26.25 0.00 245 5 -193.77 397.54 26.44 0.00 246 5 -193.79 397.57 26.46 0.00 2456 6 -193.05 398.09 26.98 0.00 156 5 -197.23 404.45 33.34 0.00 1456 6 -197.12 406.23 35.12 0.00 146 5 -198.90 407.80 36.70 0.00 16 4 -200.67 409.34 38.23 0.00 56 4 -202.12 412.24 41.13 0.00 6 3 -203.69 413.38 42.27 0.00 46 4 -202.98 413.96 42.85 0.00 456 5 -202.11 414.21 43.10 0.00 15 4 -205.52 419.03 47.92 0.00 14 4 -205.77 419.54 48.44 0.00 145 5 -205.16 420.32 49.21 0.00 1 3 -207.36 420.72 49.61 0.00 (Null) 2 -211.87 427.74 56.63 0.00 4 3 -211.42 428.84 57.73 0.00 5 3 -211.48 428.96 57.85 0.00 45 4 -211.34 430.68 59.57 0.00 Term codes: ALT GRAZE log10(AREA) log10(DIST) log10(LDIST) YR.ISOL 1 2 3 4 5 6 Model-averaged coefficients: (full average) Estimate Std. Error Adjusted SE z value Pr(>|z|) (Intercept) -102.20213 115.00849 116.06223 0.881 0.379 GRAZE -1.73394 1.18371 1.19557 1.450 0.147 log10(AREA) 7.54507 1.44065 1.47013 5.132 3e-07 *** YR.ISOL 0.06195 0.05682 0.05735 1.080 0.280 ALT 0.01068 0.01960 0.01986 0.538 0.591 log10(LDIST) -0.52644 1.33863 1.36066 0.387 0.699 log10(DIST) -0.51843 1.59104 1.61979 0.320 0.749 (conditional average) Estimate Std. Error Adjusted SE z value Pr(>|z|) (Intercept) -102.20213 115.00849 116.06223 0.881 0.3785 GRAZE -2.11307 0.95206 0.96995 2.179 0.0294 * log10(AREA) 7.54513 1.44050 1.46999 5.133 3e-07 *** YR.ISOL 0.08826 0.04772 0.04862 1.815 0.0695 . ALT 0.02531 0.02323 0.02376 1.065 0.2868 log10(LDIST) -1.49522 1.90814 1.95190 0.766 0.4437 log10(DIST) -1.58387 2.45890 2.51559 0.630 0.5289 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1confint(loyn.av)
2.5 % 97.5 % (Intercept) -329.67991528 125.27564917 GRAZE -4.01414314 -0.21200237 log10(AREA) 4.66400477 10.42625188 YR.ISOL -0.00703386 0.18356296 ALT -0.02125843 0.07188093 log10(LDIST) -5.32086871 2.33043584 log10(DIST) -6.51434345 3.34659824
- The model that you would consider to be the most parsimonious would be the model containing which terms?
- Use the model averaging to estimate the regression coefficients for each term.
Predictor: Estimate SE Lower 95% CI Upper 95% CI log10 patch distance log10 large patch distance log10 fragment area Grazing intensity Altitude Years of isolation Intercept
- Write out the full predictive model relating the abundance of forest birds to habitat characteristics based on:
- the model averaging
- refitting the most parsimonious model
Show code
loyn.lm1 <- lm(ABUND ~ log10(AREA) + GRAZE + YR.ISOL, data = loyn) summary(loyn.lm1)
Call: lm(formula = ABUND ~ log10(AREA) + GRAZE + YR.ISOL, data = loyn) Residuals: Min 1Q Median 3Q Max -14.5159 -3.8136 0.2027 3.1271 14.5542 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -134.26065 86.39085 -1.554 0.1262 log10(AREA) 7.16617 1.27260 5.631 7.32e-07 *** GRAZE -1.90216 0.87447 -2.175 0.0342 * YR.ISOL 0.07835 0.04340 1.805 0.0768 . --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6.311 on 52 degrees of freedom Multiple R-squared: 0.6732, Adjusted R-squared: 0.6544 F-statistic: 35.71 on 3 and 52 DF, p-value: 1.135e-12
Q2-7. Examine the partial effects plots.Show added variance plots (car) codelibrary(car) avPlots(loyn.lm1, ask = F)
 Show allEffects (effects) code
Show allEffects (effects) codelibrary(effects) plot(allEffects(loyn.lm1, default.levels = 1000, partial.resid = TRUE), ask = F)

# Note, the trend with AREA is plotted on a linear scale # despite being a log transformed predictor consequently the # trend appears non-linear plot(allEffects(loyn.lm1, default.levels = 1000, partial.resid = TRUE), transform.x = list(AREA = c(trans = log10, inverse = function(x) 10^x)), ticks.x = list(AREA = list(at = as.vector(c(1, 5) %o% 10^(-1:2)))), ask = F)
 Show ggeffect (ggeffects) code
Show ggeffect (ggeffects) codelibrary(ggeffects) g = ggeffect(loyn.lm1) %>% plot do.call("grid.arrange", g)
 Show ggpredict (ggpredict) code
Show ggpredict (ggpredict) codelibrary(ggeffects) g = ggpredict(loyn.lm1) %>% plot do.call("grid.arrange", g)
 Show ggemmeans (ggpredict) code
Show ggemmeans (ggpredict) codelibrary(ggeffects) grid.arrange(ggemmeans(loyn.lm1, ~AREA) %>% plot, ggemmeans(loyn.lm1, ~GRAZE) %>% plot, ggemmeans(loyn.lm1, ~YR.ISOL) %>% plot)

- How a more flexible figure.
Show predict code
newdata = with(loyn, rbind(data.frame(Var = "AREA", AREA = seq(min(AREA), max(AREA), len = 100), GRAZE = mean(GRAZE), YR.ISOL = mean(YR.ISOL)), data.frame(Var = "GRAZE", AREA = mean(AREA), GRAZE = seq(min(GRAZE), max(GRAZE), len = 100), YR.ISOL = mean(YR.ISOL)), data.frame(Var = "YR.ISOL", AREA = mean(AREA), GRAZE = mean(GRAZE), YR.ISOL = seq(min(YR.ISOL), max(YR.ISOL), len = 100)))) fit <- predict(loyn.lm1, newdata = newdata, interval = "confidence") fit <- cbind(newdata, fit) head(fit)
Var AREA GRAZE YR.ISOL fit lwr upr 1 AREA 0.10000 2.982143 1949.75 5.669721 0.4540249 10.88542 2 AREA 17.98788 2.982143 1949.75 21.829281 19.9466085 23.71195 3 AREA 35.87576 2.982143 1949.75 23.977848 21.6553721 26.30032 4 AREA 53.76364 2.982143 1949.75 25.236854 22.5868714 27.88684 5 AREA 71.65152 2.982143 1949.75 26.130739 23.2284951 29.03298 6 AREA 89.53939 2.982143 1949.75 26.824343 23.7179571 29.93073
# calculated the partial observed values partial.obs <- with(loyn, rbind(data.frame(Var = "AREA", AREA = AREA, GRAZE = mean(GRAZE), YR.ISOL = mean(YR.ISOL)), data.frame(Var = "GRAZE", AREA = mean(AREA), GRAZE = GRAZE, YR.ISOL = mean(YR.ISOL)), data.frame(Var = "YR.ISOL", AREA = mean(AREA), GRAZE = mean(GRAZE), YR.ISOL = YR.ISOL))) partial.obs <- cbind(partial.obs, fit = predict(loyn.lm1, newdata = partial.obs)) partial.obs = partial.obs %>% mutate(presid = fit + resid(loyn.lm1)) head(partial.obs)
Var AREA GRAZE YR.ISOL fit presid 1 AREA 0.1 2.982143 1949.75 5.669721 2.001867 2 AREA 0.5 2.982143 1949.75 10.678656 8.169284 3 AREA 0.5 2.982143 1949.75 10.678656 9.236347 4 AREA 1.0 2.982143 1949.75 12.835887 15.860729 5 AREA 1.0 2.982143 1949.75 12.835887 20.125990 6 AREA 1.0 2.982143 1949.75 12.835887 12.939082
fit = fit %>% mutate(Value = case_when(Var == "AREA" ~ AREA, Var == "GRAZE" ~ GRAZE, Var == "YR.ISOL" ~ YR.ISOL)) partial.obs = partial.obs %>% mutate(Value = case_when(Var == "AREA" ~ AREA, Var == "GRAZE" ~ GRAZE, Var == "YR.ISOL" ~ YR.ISOL)) ggplot(fit, aes(y = fit, x = Value)) + geom_line() + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.3) + geom_point(data = partial.obs, aes(y = presid)) + facet_wrap(~Var, scales = "free_x") + theme_bw()

## Or if we need a bit more finesse Area p1 <- ggplot(data = fit %>% filter(Var == "AREA"), aes(y = fit, x = AREA)) + geom_point(data = partial.obs %>% filter(Var == "AREA"), aes(y = presid, x = AREA), color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Bird abundance") + scale_x_continuous(expression(Fragment ~ area ~ (ha)), trans = scales::log_trans(base = 10)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) ### Grazing p2 <- ggplot(data = fit %>% filter(Var == "GRAZE"), aes(y = fit, x = GRAZE)) + geom_point(data = partial.obs %>% filter(Var == "GRAZE"), aes(y = presid, x = GRAZE), color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Bird abundance") + scale_x_continuous(expression(Grazing ~ intensity)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) ### Grazing p3 <- ggplot(data = fit %>% filter(Var == "YR.ISOL"), aes(y = fit, x = YR.ISOL)) + geom_point(data = partial.obs %>% filter(Var == "YR.ISOL"), aes(y = presid, x = YR.ISOL), color = "grey") + geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Bird abundance") + scale_x_continuous(expression(Year ~ isolated)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) grid.arrange(p1, p2, p3, ncol = 2)
 Show emmeans code
Show emmeans code## It is best to generate the partial trends one at a time ## AREA loyn.list = with(loyn, list(AREA = seq(min(AREA), max(AREA), len = 100), GRAZE = mean(GRAZE), YR.ISOL = mean(YR.ISOL))) loyn.grid = ref_grid(loyn.lm1, ~AREA, at = loyn.list, cov.reduce = FALSE) newdata = confint(loyn.grid) head(newdata)
AREA GRAZE YR.ISOL prediction SE df lower.CL upper.CL 1 0.10000 2.982143 1949.75 5.669721 2.599210 52 0.4540249 10.88542 2 17.98788 2.982143 1949.75 21.829281 0.938218 52 19.9466085 23.71195 3 35.87576 2.982143 1949.75 23.977848 1.157392 52 21.6553721 26.30032 4 53.76364 2.982143 1949.75 25.236854 1.320603 52 22.5868714 27.88684 5 71.65152 2.982143 1949.75 26.130739 1.446315 52 23.2284951 29.03298 6 89.53939 2.982143 1949.75 26.824343 1.548048 52 23.7179571 29.93073
# calculated the partial observed values partial.obs <- ref_grid(loyn.lm1, ~AREA, cov.reduce = FALSE, at = list(AREA = loyn$AREA, GRAZE = mean(loyn$GRAZE), YR.ISOL = mean(loyn$YR.ISOL))) %>% summary %>% mutate(presid = prediction + as.vector(resid(loyn.lm1))) p1 <- ggplot(data = newdata, aes(y = prediction, x = AREA)) + geom_point(data = partial.obs, aes(y = presid, x = AREA), color = "grey") + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Bird abundance") + scale_x_continuous(expression(Fragment ~ area ~ (ha)), trans = scales::log_trans(base = 10)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) ### Grazing loyn.list = with(loyn, list(GRAZE = seq(min(GRAZE), max(GRAZE), len = 100), AREA = mean(AREA), YR.ISOL = mean(YR.ISOL))) loyn.grid = ref_grid(loyn.lm1, ~GRAZE, at = loyn.list, cov.reduce = FALSE) newdata = confint(loyn.grid) head(newdata)
AREA GRAZE YR.ISOL prediction SE df lower.CL upper.CL 1 69.26964 1.000000 1949.75 29.79587 1.728280 52 26.32782 33.26391 2 69.26964 1.040404 1949.75 29.71901 1.705234 52 26.29721 33.14081 3 69.26964 1.080808 1949.75 29.64216 1.682615 52 26.26574 33.01857 4 69.26964 1.121212 1949.75 29.56530 1.660439 52 26.23339 32.89722 5 69.26964 1.161616 1949.75 29.48845 1.638725 52 26.20010 32.77679 6 69.26964 1.202020 1949.75 29.41159 1.617491 52 26.16586 32.65733
# calculated the partial observed values partial.obs <- ref_grid(loyn.lm1, ~GRAZE, cov.reduce = FALSE, at = list(GRAZE = loyn$GRAZE, AREA = mean(loyn$AREA), YR.ISOL = mean(loyn$YR.ISOL))) %>% summary %>% mutate(presid = prediction + as.vector(resid(loyn.lm1))) p2 <- ggplot(data = newdata, aes(y = prediction, x = GRAZE)) + geom_point(data = partial.obs, aes(y = presid, x = GRAZE), color = "grey") + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Bird abundance") + scale_x_continuous(expression(Grazing ~ intensity)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) ### Grazing loyn.list = with(loyn, list(YR.ISOL = seq(min(YR.ISOL), max(YR.ISOL), len = 100), AREA = mean(AREA), GRAZE = mean(GRAZE))) loyn.grid = ref_grid(loyn.lm1, ~YR.ISOL, at = loyn.list, cov.reduce = FALSE) newdata = confint(loyn.grid) head(newdata)
AREA GRAZE YR.ISOL prediction SE df lower.CL upper.CL 1 69.26964 2.982143 1890.000 21.34392 2.837729 52 15.64960 27.03824 2 69.26964 2.982143 1890.869 21.41199 2.805184 52 15.78297 27.04100 3 69.26964 2.982143 1891.737 21.48005 2.772769 52 15.91608 27.04402 4 69.26964 2.982143 1892.606 21.54811 2.740490 52 16.04892 27.04731 5 69.26964 2.982143 1893.475 21.61618 2.708351 52 16.18148 27.05088 6 69.26964 2.982143 1894.343 21.68424 2.676357 52 16.31374 27.05475
# calculated the partial observed values partial.obs <- ref_grid(loyn.lm1, ~YR.ISOL, cov.reduce = FALSE, at = list(YR.ISOL = loyn$YR.ISOL, AREA = mean(loyn$AREA), GRAZE = mean(loyn$GRAZE))) %>% summary %>% mutate(presid = prediction + as.vector(resid(loyn.lm1))) p3 <- ggplot(data = newdata, aes(y = prediction, x = YR.ISOL)) + geom_point(data = partial.obs, aes(y = presid, x = YR.ISOL), color = "grey") + geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), fill = "blue", alpha = 0.2) + geom_line() + scale_y_continuous("Bird abundance") + scale_x_continuous(expression(Year ~ isolation)) + theme_classic() + theme(axis.title.y = element_text(vjust = 1, size = rel(1.25)), axis.title.x = element_text(vjust = -1, size = rel(1.25)), plot.margin = unit(c(0.5, 0.5, 1, 1), "lines")) grid.arrange(p1, p2, p3, ncol = 2)

- As an arguably more sensible approach to model selection,
lets propose a small set of plausible candidate models for comparison. In the absence of any other motives or criteria,
I am going to propose we explore the following:
- fragment area and grazing intensity - habitat model
- atch distance - connectivity model
- years of isolation - history model
- fragment area, grazing intensity and patch distance - habitat/connectivity model
Show glht codeloyn.lmH <- lm(ABUND ~ log10(AREA) + GRAZE, data = loyn) loyn.lmC <- lm(ABUND ~ log10(DIST), data = loyn) loyn.lmY <- lm(ABUND ~ YR.ISOL, data = loyn) loyn.lmHC <- lm(ABUND ~ log10(DIST) + log10(AREA) + GRAZE, data = loyn) library(MuMIn) AICc(loyn.lmH, loyn.lmC, loyn.lmY, loyn.lmHC)
df AICc loyn.lmH 4 373.2977 loyn.lmC 3 429.2976 loyn.lmY 3 413.8419 loyn.lmHC 5 374.3646
Since none of the predictor variables are highly correlated to one another, we can include all in the linear model fitting.
In this question, we are not so interested in hypothesis testing. That is, we are not trying to determine if there is a significant effect of one or more predictor variables on the abundance of forest birds. Rather, we wish to either (or both);
Polynomial regression
Rademaker and Cerqueira (2006), compiled data from the literature on the reproductive traits of opossoms (Didelphis) so as to investigate latitudinal trends in reproductive output. In particular, they were interested in whether there were any patterns in mean litter size across a longitudinal gradient from 44oN to 34oS. Analyses of data compiled from second hand sources are called metaanalyses and are very usefull at revealing overal trends across a range of studies.
Download Rademaker data set| Format of rademaker.csv data files | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
rademaker <- read.table("../downloads/data/rademaker.csv", header = T, sep = ",", strip.white = T) head(rademaker)
SPECIES LATITUDE L.Y MAOP MLS DB REFERENCE 1 D.v. 44.0 2.0 16.8 8.4 M-Feb-Sept Tyndale-Biscoe and Mackenzie (1976) 2 D.v. 41.0 1.5 14.1 9.4 E-Mar-Sept Hossler et al. (1994) 3 D.v. 41.5 NA NA 8.6 Reynolds (1952) 4 D.v. 41.0 2.0 18.0 9.0 M-Feb-Sept Wiseman and Hendrickson (1950) 5 D.v. 40.0 2.0 15.8 7.9 M-Feb-Sept Sanderson (1961) 6 D.v. 39.0 2.0 17.8 8.9 E-Feb-Sept Reynolds (1945)
The main variables of interest in this data set are MLS (mean litter size) and LATITUDE. The other variables were included so as to enable you to see how meta data might be collected and collated from a number of other sources.
The relationship between two continuous variables can be analyzed by simple linear regression. Before performing the analysis we need to check the assumptions. To evaluate the assumptions of linearity, normality and homogeneity of variance, construct a scatterplot
of MLS against LATITUDE including a lowess smoother and boxplots on the axes. (HINT)library(car) scatterplot(MLS ~ LATITUDE, data = rademaker)
- Is there any evidence that any of the regular assumptions of simple linear regression are likely to be violated?
- How would you describe the residual plot?
- If the assumptions are otherwise met, perform the second order polynomial regression analysis (
fit the quadratic polynomial model
), examine the output, and use the information to construct the regression equation relating the number of mean litter size to latitude:
Show code
rademaker.lm <- lm(MLS ~ LATITUDE + I(LATITUDE^2), data = rademaker) rademaker.lm
Call: lm(formula = MLS ~ LATITUDE + I(LATITUDE^2), data = rademaker) Coefficients: (Intercept) LATITUDE I(LATITUDE^2) 5.391575 -0.029758 0.002448DV = intercept + slope1 x IV2 + slope2 x IV Mean litter size = + x latitude2 + x latitude - In polynomial regression, there are two hypotheses of interest. Firstly, as there are two slopes, we are now interested in
whether the individual slopes are equal to one another and to zero
(that is, does the overall model explain our data better than just a horizontal line (no trend). Secondly, we are interested in whether the
second order polynomial model fits the data any better than a simple first order (straight-line) model
. Test these null hypotheses.
Show code
summary(rademaker.lm)
Call: lm(formula = MLS ~ LATITUDE + I(LATITUDE^2), data = rademaker) Residuals: Min 1Q Median 3Q Max -2.3335 -0.6117 -0.1748 0.4688 2.4592 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 5.391574 0.290622 18.552 < 2e-16 *** LATITUDE -0.029758 0.008385 -3.549 0.00115 ** I(LATITUDE^2) 0.002448 0.000368 6.653 1.24e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1.019 on 34 degrees of freedom Multiple R-squared: 0.5711, Adjusted R-squared: 0.5459 F-statistic: 22.64 on 2 and 34 DF, p-value: 5.624e-07rademaker.lm1 <- lm(MLS ~ LATITUDE, data = rademaker) anova(rademaker.lm, rademaker.lm1)
Analysis of Variance Table Model 1: MLS ~ LATITUDE + I(LATITUDE^2) Model 2: MLS ~ LATITUDE Res.Df RSS Df Sum of Sq F Pr(>F) 1 34 35.322 2 35 81.311 -1 -45.989 44.267 1.237e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
- The slopes
significantly different from one another and to 0 (F =
, df =
,
, P =
)
- The second order polynomial regression model
fit the data significantly better than a first order (straight line) regression model (F =
, df =
,
, P =
)
- The slopes
- What are your conclusions (statistical and biological)?
- Such an outcome might also be accompanied by a scatterpoint that illustrates the relationship between the mean litter size and latitude. Construct a scatterplot without a smoother or marginal boxplots (HINT). Include a quadratic (second order) trendline on this graph (HINT).
Show code
opar <- par(mfrow = c(2, 2)) # first plot trend with 95% confidence intervals opar1 <- par(mar = c(5, 5, 0, 0)) plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n") points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16) xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000)) ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), interval = "confidence") points(ys[, "fit"] ~ xs, col = "black", type = "l") points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2) points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2) axis(1) mtext("Lattitude", 1, line = 3, cex = 1.2) axis(2, las = 1) mtext(expression(paste("Mean litter size (", phantom() %+-% 95, "% CI)")), 2, line = 3, cex = 1.2) box(bty = "l") par(opar1) # second plot trend with 95% prediction intervals opar1 <- par(mar = c(5, 5, 0, 0)) plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n") points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16) xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000)) ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), interval = "prediction") points(ys[, "fit"] ~ xs, col = "black", type = "l") points(ys[, "lwr"] ~ xs, col = "black", type = "l", lty = 2) points(ys[, "upr"] ~ xs, col = "black", type = "l", lty = 2) axis(1) mtext("Lattitude", 1, line = 3, cex = 1.2) axis(2, las = 1) mtext(expression(paste("Mean litter size (", phantom() %+-% 95, "% PI)")), 2, line = 3, cex = 1.2) box(bty = "l") par(opar1) # third plot trend with standard error opar1 <- par(mar = c(5, 5, 0, 0)) plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n") points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16) xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000)) ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), se.fit = T) points(ys$fit ~ xs, col = "black", type = "l") points(ys$fit - ys$se.fit ~ xs, col = "black", type = "l", lty = 2) points(ys$fit + ys$se.fit ~ xs, col = "black", type = "l", lty = 2) axis(1) mtext("Lattitude", 1, line = 3, cex = 1.2) axis(2, las = 1) mtext(expression(paste("Mean litter size (", phantom() %+-% 1, "SE)")), 2, line = 3, cex = 1.2) box(bty = "l") par(opar1) # forth plot trend with standard error opar1 <- par(mar = c(5, 5, 0, 0)) plot(MLS ~ LATITUDE, data = rademaker, ann = F, axes = F, type = "n") points(MLS ~ LATITUDE, data = rademaker, col = "grey", pch = 16) xs <- with(rademaker, seq(min(LATITUDE), max(LATITUDE), l = 1000)) ys <- predict(rademaker.lm, data.frame(LATITUDE = xs), se.fit = T) points(ys$fit ~ xs, col = "black", type = "l") points(ys$fit - 2 * ys$se.fit ~ xs, col = "black", type = "l", lty = 2) points(ys$fit + 2 * ys$se.fit ~ xs, col = "black", type = "l", lty = 2) axis(1) mtext("Lattitude", 1, line = 3, cex = 1.2) axis(2, las = 1) mtext(expression(paste("Mean litter size (", phantom() %+-% 2, "SE)")), 2, line = 3, cex = 1.2) box(bty = "l")

par(opar1) par(opar)
To get an appreciation of what a residual plot would look like when there is some evidence that the linearity assumption has been violated, perform the simple linear regression (by fitting a linear model)
purely for the purpose of examining the regression diagnostics (particularly the residual plot)# fit the model rademaker.lm <- lm(MLS ~ LATITUDE, data = rademaker) # setup a 2x6 plotting device with small margins par(mfrow = c(2, 3), oma = c(0, 0, 2, 0)) plot(rademaker.lm, ask = F, which = 1:6)
influence.measures(rademaker.lm)
Influence measures of
lm(formula = MLS ~ LATITUDE, data = rademaker) :
dfb.1_ dfb.LATI dffit cov.r cook.d hat inf
1 0.094628 0.201743 0.24356 1.118 3.00e-02 0.0861
2 0.185879 0.354286 0.43929 1.007 9.30e-02 0.0773
3 0.114708 0.222842 0.27499 1.093 3.79e-02 0.0787
4 0.150114 0.286119 0.35477 1.053 6.20e-02 0.0773
5 0.057329 0.105129 0.13168 1.131 8.87e-03 0.0745
6 0.144545 0.254834 0.32264 1.057 5.15e-02 0.0719
7 0.016273 0.028690 0.03632 1.141 6.79e-04 0.0719
8 0.041857 0.072336 0.09210 1.133 4.35e-03 0.0705
9 0.000616 0.001001 0.00130 1.135 8.68e-07 0.0667
10 -0.085085 -0.111051 -0.15544 1.095 1.23e-02 0.0552
11 -0.031444 -0.039138 -0.05583 1.116 1.60e-03 0.0531
12 -0.031444 -0.039138 -0.05583 1.116 1.60e-03 0.0531
13 -0.076087 -0.090187 -0.13132 1.096 8.79e-03 0.0512
14 0.049708 0.009612 0.05345 1.084 1.47e-03 0.0279
15 -0.278150 0.002187 -0.28314 0.925 3.80e-02 0.0270
16 -0.302666 0.002380 -0.30809 0.899 4.44e-02 0.0270
17 -0.117656 0.000925 -0.11977 1.057 7.27e-03 0.0270
18 -0.267330 0.012377 -0.27036 0.939 3.49e-02 0.0271
19 -0.255295 0.011820 -0.25819 0.951 3.21e-02 0.0271
20 -0.231553 0.010721 -0.23418 0.973 2.67e-02 0.0271
21 -0.317516 0.020735 -0.32026 0.887 4.76e-02 0.0271
22 -0.280153 0.018295 -0.28257 0.927 3.79e-02 0.0271
23 -0.046707 0.026910 -0.05012 1.097 1.29e-03 0.0380
24 0.021524 -0.017109 0.02524 1.115 3.28e-04 0.0500
25 0.333540 -0.265117 0.39106 0.947 7.25e-02 0.0500
26 0.234031 -0.186021 0.27439 1.027 3.72e-02 0.0500
27 -0.082266 0.069901 -0.09893 1.109 5.01e-03 0.0540
28 0.118457 -0.103838 0.14428 1.100 1.06e-02 0.0561
29 -0.002004 0.001757 -0.00244 1.123 3.07e-06 0.0561
30 0.051315 -0.044982 0.06250 1.118 2.01e-03 0.0561
31 0.231543 -0.209119 0.28565 1.043 4.04e-02 0.0582
32 0.066101 -0.059700 0.08155 1.118 3.41e-03 0.0582
33 0.067544 -0.062775 0.08440 1.121 3.65e-03 0.0605
34 0.311295 -0.297381 0.39396 0.991 7.48e-02 0.0628
35 0.180242 -0.172186 0.22811 1.081 2.62e-02 0.0628
36 -0.039381 0.039625 -0.05112 1.134 1.34e-03 0.0677
37 0.023962 -0.028153 0.03388 1.160 5.91e-04 0.0873
For this sort of trend that is clearly non-linear (yet the boxplots suggest normal data), transformations are of no use. Therefore, rather than attempt to model the data on a simple linear relationship (straight line), it is better to attempt to model the data on a curvilinear linear relationship (curved line). Note it is important to make the distinction between
line (relationship) linearity and model linearity