Workshop 9.3b - Mixed effects (Multilevel models): Randomized block designs (Bayesian)
30 Jan 2015
Randomized block and simple repeated measures ANOVA (Mixed effects) references
- McCarthy (2007) - Chpt ?
- Kery (2010) - Chpt ?
- Gelman & Hill (2007) - Chpt ?
- Logan (2010) - Chpt 13
- Quinn & Keough (2002) - Chpt 10
Randomized block design
A plant pathologist wanted to examine the effects of two different strengths of tobacco virus on the number of lesions on tobacco leaves. She knew from pilot studies that leaves were inherently very variable in response to the virus. In an attempt to account for this leaf to leaf variability, both treatments were applied to each leaf. Eight individual leaves were divided in half, with half of each leaf inoculated with weak strength virus and the other half inoculated with strong virus. So the leaves were blocks and each treatment was represented once in each block. A completely randomised design would have had 16 leaves, with 8 whole leaves randomly allocated to each treatment.
Download Tobacco data set
| Format of tobacco.csv data files | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
Open the tobacco data file.
tobacco <- read.table('../downloads/data/tobacco.csv', header=T, sep=',', strip.white=T) head(tobacco)
LEAF TREATMENT NUMBER 1 L1 Strong 35.90 2 L1 Weak 25.02 3 L2 Strong 34.12 4 L2 Weak 23.17 5 L3 Strong 35.70 6 L3 Weak 24.12
To appreciate the difference between this design (Complete Randomized Block) in which there is a single within Group effect (Treatment) and a nested design (in which there are between group effects), I will illustrate the current design diagramatically.
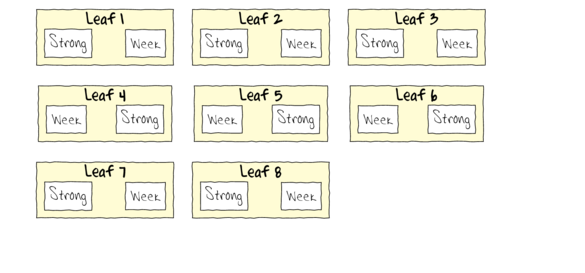
- Note that each level of the Treatment (Strong and Week) are applied to each Leaf (Block)
- Note that Treatments are randomly applied
- The Treatment effect is the mean difference between Treatment pairs per leaf
- Blocking in this way is very useful when spatial or temporal heterogeneity is likely to add noise that could make it difficualt to detect a difference between Treatments. Hence it is a way of experimentally reducing unexplained variation (compared to nesting which involves statistical reduction of unexplained variation).
Exploratory data analysis has indicated that the response variable could be normalized via a forth-root transformation.
- Fit a model for the Randomized Complete Block
- Full Effects parameterization - random intercepts model (JAGS)
number of lesionsi = βSite j(i) + εi where ε ∼ N(0,σ2)
View full effects parameterization (JAGS) codemodelString= ## write the model to a text file (I suggest you alter the path to somewhere more relevant ## to your system!) writeLines(modelString,con="../downloads/BUGSscripts/ws9.3bQ1.1a.txt") tobacco.list <- with(tobacco, list(number=NUMBER, treatment=as.numeric(TREATMENT), leaf=as.numeric(LEAF), n=nrow(tobacco), nTreat=length(levels(as.factor(TREATMENT))), nLeaf=length(levels(as.factor(LEAF))) ) ) params <- c("perc.Treat","p.decline","p.decline5","p.decline10","p.decline20","p.decline50","p.decline100","Treatment.means","beta.leaf","beta.treatment","sigma.res","sigma.leaf","sd.Resid","sd.Leaf","sd.Treatment") burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) library(coda) ## tobacco.r2jags.a <- jags(data=tobacco.list, inits=NULL,#inits=list(inits,inits,inits), # since there are three chains parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.3bQ1.1a.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 151 Initializing model
print(tobacco.r2jags.a)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.3bQ1.1a.txt", fit using jags, 3 chains, each with 1e+05 iterations (first 3000 discarded), n.thin = 100 n.sims = 2910 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff Treatment.means[1] 34.685 2.685 29.149 33.053 34.653 36.412 40.012 1.001 2900 Treatment.means[2] 26.778 2.742 21.239 25.041 26.811 28.578 32.220 1.001 2900 beta.leaf[1] 34.685 2.685 29.149 33.053 34.653 36.412 40.012 1.001 2900 beta.leaf[2] 33.656 2.814 27.994 31.863 33.737 35.492 39.055 1.001 2500 beta.leaf[3] 34.382 2.683 29.202 32.663 34.407 36.145 39.762 1.001 2900 beta.leaf[4] 32.910 2.823 27.384 31.022 32.955 34.858 38.278 1.001 2900 beta.leaf[5] 33.941 2.682 28.638 32.234 33.938 35.656 39.405 1.004 590 beta.leaf[6] 37.844 3.105 31.836 35.758 37.911 39.901 43.728 1.001 2900 beta.leaf[7] 39.568 3.597 32.746 36.978 39.646 42.186 46.379 1.001 2900 beta.leaf[8] 32.731 3.012 26.898 30.712 32.712 34.781 38.524 1.001 2600 beta.treatment[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 beta.treatment[2] -7.907 2.378 -12.693 -9.354 -7.896 -6.444 -3.224 1.001 2900 p.decline 0.999 0.037 1.000 1.000 1.000 1.000 1.000 1.029 2900 p.decline10 0.974 0.161 0.000 1.000 1.000 1.000 1.000 1.001 2900 p.decline100 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 p.decline20 0.690 0.463 0.000 0.000 1.000 1.000 1.000 1.001 2900 p.decline5 0.993 0.085 1.000 1.000 1.000 1.000 1.000 1.003 2900 p.decline50 0.000 0.019 0.000 0.000 0.000 0.000 0.000 1.291 2900 perc.Treat -22.712 6.381 -34.921 -26.669 -22.942 -18.850 -9.835 1.001 2900 sd.Leaf 3.243 1.482 0.318 2.225 3.357 4.302 5.890 1.002 2900 sd.Resid 6.540 0.000 6.540 6.540 6.540 6.540 6.540 1.000 1 sd.Treatment 2.042 0.612 0.832 1.664 2.039 2.415 3.277 1.001 2900 sigma.leaf 3.963 2.318 0.345 2.409 3.702 5.176 9.366 1.002 2900 sigma.res 4.679 1.319 2.690 3.727 4.477 5.387 7.862 1.001 2200 deviance 92.407 6.520 80.987 87.336 92.077 97.216 105.118 1.001 2900 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 21.3 and DIC = 113.7 DIC is an estimate of expected predictive error (lower deviance is better).tobacco.mcmc.a <- tobacco.r2jags.a$BUGSoutput$sims.matrix
Note that the Leaf β are not actually the leaf means. Rather they are the intercepts for each leaf (since we have fit a random intercepts model). They represent the value of the first Treatment level (Strong) within each Leaf.
The Treatment effect thus represents the mean of the differences between the second Treatment level (Week) and these intercepts.
Indeed, the analysis assumes that there is no real interactions between the Leafs (Blocks) and the Treatment effects (within Blocks) - otherwise the mean Treatment effect would be a over simplification of the true nature of the populations. The presence of such an interaction would indicate that the Blocks (Leafs) do not all represent the same population.
View full codemodelString= ## write the model to a text file (I suggest you alter the path to somewhere more relevant ## to your system!) writeLines(modelString,con="../downloads/BUGSscripts/ws9.3bQ1.1a1.txt") tobacco.list <- with(tobacco, list(number=NUMBER, treatment=as.numeric(TREATMENT), leaf=as.numeric(LEAF), n=nrow(tobacco), nTreat=length(levels(as.factor(TREATMENT))), nLeaf=length(levels(as.factor(LEAF))) ) ) params <- c("Leaf.means","Treatment.means","beta","beta.leaf","beta.treatment","sigma.res","sd.Leaf","sd.Treatment","sd.Int","sd.Resid") adaptSteps = 1000 burnInSteps = 200 nChains = 3 numSavedSteps = 5000 thinSteps = 10 nIter = ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) ## tobacco.r2jags2 <- jags(data=tobacco.list, inits=NULL,#inits=list(inits,inits,inits), # since there are three chains parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.3bQ1.1a1.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 185 Initializing model
print(tobacco.r2jags2)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.3bQ1.1a1.txt", fit using jags, 3 chains, each with 16667 iterations (first 200 discarded), n.thin = 10 n.sims = 4941 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff Leaf.means[1] 30.450 0.532 30.303 30.448 30.459 30.470 30.614 1.290 3600 Leaf.means[2] 28.655 1.204 28.471 28.632 28.643 28.654 28.806 1.286 4900 Leaf.means[3] 29.887 1.478 29.736 29.901 29.912 29.923 30.083 1.289 4000 Leaf.means[4] 27.075 1.181 26.895 27.070 27.082 27.092 27.231 1.286 4900 Leaf.means[5] 29.108 1.018 28.939 29.092 29.103 29.114 29.282 1.286 4900 Leaf.means[6] 36.349 0.653 36.156 36.349 36.360 36.371 36.538 1.290 3500 Leaf.means[7] 39.603 0.588 39.436 39.593 39.604 39.615 39.770 1.280 4900 Leaf.means[8] 26.843 0.776 26.659 26.830 26.841 26.852 27.026 1.284 4900 Treatment.means[1] 34.932 0.565 34.837 34.934 34.940 34.945 35.016 1.290 4000 Treatment.means[2] 27.060 0.418 26.981 27.055 27.061 27.066 27.155 1.288 4900 beta[1,1] 35.898 0.539 35.599 35.882 35.898 35.913 36.124 1.260 4900 beta[2,1] 34.126 1.993 33.856 34.101 34.117 34.133 34.333 1.286 4900 beta[3,1] 35.652 2.193 35.437 35.686 35.702 35.717 35.944 1.289 1900 beta[4,1] 26.214 1.867 25.945 26.208 26.224 26.240 26.436 1.287 4900 beta[5,1] 33.018 0.754 32.745 33.001 33.017 33.032 33.275 1.257 4900 beta[6,1] 36.723 0.714 36.450 36.712 36.728 36.743 36.974 1.285 4600 beta[7,1] 44.718 0.766 44.459 44.708 44.723 44.738 44.966 1.284 4800 beta[8,1] 33.107 0.654 32.867 33.094 33.110 33.125 33.395 1.274 4900 beta[1,2] 25.002 1.325 24.810 25.005 25.021 25.036 25.278 1.285 2900 beta[2,2] 23.184 1.023 22.912 23.152 23.168 23.184 23.419 1.282 4100 beta[3,2] 24.121 1.202 23.877 24.106 24.122 24.137 24.332 1.274 4900 beta[4,2] 27.935 0.694 27.679 27.923 27.939 27.954 28.161 1.242 4900 beta[5,2] 25.198 1.848 24.952 25.174 25.189 25.205 25.484 1.286 4900 beta[6,2] 35.975 0.974 35.719 35.978 35.993 36.008 36.267 1.279 2500 beta[7,2] 34.487 1.033 34.256 34.469 34.485 34.500 34.735 1.277 4900 beta[8,2] 20.579 1.255 20.321 20.557 20.572 20.587 20.831 1.284 4900 beta.leaf[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 beta.leaf[2] -1.795 1.636 -2.073 -1.832 -1.816 -1.801 -1.583 1.286 4300 beta.leaf[3] -0.564 1.164 -0.821 -0.564 -0.548 -0.532 -0.299 1.282 4900 beta.leaf[4] -3.375 1.487 -3.630 -3.393 -3.377 -3.362 -3.179 1.286 4900 beta.leaf[5] -1.342 0.858 -1.593 -1.372 -1.356 -1.341 -1.077 1.274 3200 beta.leaf[6] 5.899 0.738 5.635 5.886 5.901 5.917 6.155 1.274 4900 beta.leaf[7] 9.153 0.843 8.915 9.129 9.145 9.160 9.406 1.280 4900 beta.leaf[8] -3.607 1.118 -3.879 -3.634 -3.618 -3.603 -3.370 1.281 4900 beta.treatment[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1 beta.treatment[2] -7.872 0.861 -7.978 -7.887 -7.879 -7.871 -7.728 1.286 4900 sd.Int 2.625 0.611 2.550 2.594 2.598 2.602 2.683 1.265 500 sd.Leaf 4.598 0.857 4.517 4.564 4.568 4.572 4.656 1.285 530 sd.Resid 6.540 0.000 6.540 6.540 6.540 6.540 6.540 1.000 1 sd.Treatment 5.578 0.488 5.466 5.566 5.571 5.577 5.641 1.254 4900 sigma.res 47.566 29.437 1.450 22.068 46.182 73.601 96.953 1.049 86 deviance -66.217 36.598 -105.078 -91.771 -76.891 -53.566 33.084 1.048 87 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 654.3 and DIC = 588.1 DIC is an estimate of expected predictive error (lower deviance is better).View matrix parameterization (JAGS) codemodelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau.res) mu[i] <- inprod(gamma[],Z[i,]) + inprod(beta[],X[i,]) y.err[i] <- y[i] - mu[i] } #Priors and derivatives for (i in 1:nZ) { gamma[i] ~ dnorm(mu.gamma,tau.leaf) } mu.gamma ~ dnorm(0,1.0E-06) for (i in 1:nX) { beta[i] ~ dnorm(0,1.0E-6) } Treatment.means[1] <- beta[1] Treatment.means[2] <- beta[1]+beta[2] # Half-cauchy (scale=25) priors on variance tau.res <- pow(sigma.res,-2) sigma.res <-z/sqrt(chSq) z ~ dnorm(0, .0016)I(0,) chSq ~ dgamma(0.5, 0.5) tau.leaf <- pow(sigma.leaf,-2) sigma.leaf <- z.leaf/sqrt(chSq.leaf) z.leaf ~ dnorm(0, .0016)I(0,) chSq.leaf ~ dgamma(0.5, 0.5) sd.Leaf <- sd(gamma) sd.Treatment <- sd(Treatment.means) sd.Resid <- sd(y.err) } " ## write the model to a text file (I suggest you alter the path to somewhere more relevant ## to your system!) writeLines(modelString,con="../downloads/BUGSscripts/ws9.3bQ1.1b.txt") Xmat <- model.matrix(~TREATMENT, tobacco) Zmat <- model.matrix(~LEAF, tobacco) tobacco.list <- with(tobacco, list(y=NUMBER, X=Xmat, nX=ncol(Xmat), Z=Zmat, nZ=ncol(Zmat), n=nrow(tobacco) ) ) tobacco.list
$y [1] 35.90 25.02 34.12 23.17 35.70 24.12 26.22 27.94 33.02 25.19 35.99 36.73 34.48 44.72 20.57 33.11 $X (Intercept) TREATMENTWeak 1 1 0 2 1 1 3 1 0 4 1 1 5 1 0 6 1 1 7 1 0 8 1 1 9 1 0 10 1 1 11 1 1 12 1 0 13 1 1 14 1 0 15 1 1 16 1 0 attr(,"assign") [1] 0 1 attr(,"contrasts") attr(,"contrasts")$TREATMENT [1] "contr.treatment" $nX [1] 2 $Z (Intercept) LEAFL2 LEAFL3 LEAFL4 LEAFL5 LEAFL6 LEAFL7 LEAFL8 1 1 0 0 0 0 0 0 0 2 1 0 0 0 0 0 0 0 3 1 1 0 0 0 0 0 0 4 1 1 0 0 0 0 0 0 5 1 0 1 0 0 0 0 0 6 1 0 1 0 0 0 0 0 7 1 0 0 1 0 0 0 0 8 1 0 0 1 0 0 0 0 9 1 0 0 0 1 0 0 0 10 1 0 0 0 1 0 0 0 11 1 0 0 0 0 1 0 0 12 1 0 0 0 0 1 0 0 13 1 0 0 0 0 0 1 0 14 1 0 0 0 0 0 1 0 15 1 0 0 0 0 0 0 1 16 1 0 0 0 0 0 0 1 attr(,"assign") [1] 0 1 1 1 1 1 1 1 attr(,"contrasts") attr(,"contrasts")$LEAF [1] "contr.treatment" $nZ [1] 8 $n [1] 16
params <- c("Treatment.means","gamma","beta","sigma.res","sigma.leaf","sd.Resid","sd.Leaf","sd.Treatment") burnInSteps = 3000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = ceiling((numSavedSteps * thinSteps)/nChains) library(R2jags) ## tobacco.r2jags.b <- jags(data=tobacco.list, inits=NULL,#inits=list(inits,inits,inits), # since there are three chains parameters.to.save=params, model.file="../downloads/BUGSscripts/ws9.3bQ1.1b.txt", n.chains=3, n.iter=nIter, n.burnin=burnInSteps, n.thin=thinSteps )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 288 Initializing model
print(tobacco.r2jags.b)
Inference for Bugs model at "../downloads/BUGSscripts/ws9.3bQ1.1b.txt", fit using jags, 3 chains, each with 1e+05 iterations (first 3000 discarded), n.thin = 100 n.sims = 2910 iterations saved mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff Treatment.means[1] 33.486 9.390 14.235 27.827 33.589 39.395 51.137 1.001 2900 Treatment.means[2] 25.671 9.419 6.849 19.987 25.901 31.472 43.860 1.002 2900 beta[1] 33.486 9.390 14.235 27.827 33.589 39.395 51.137 1.001 2900 beta[2] -7.815 2.377 -12.724 -9.259 -7.774 -6.342 -3.158 1.003 1200 gamma[1] 0.802 6.996 -12.693 -3.234 0.641 4.811 15.336 1.002 2900 gamma[2] -0.723 4.474 -9.263 -3.575 -0.895 1.947 8.839 1.002 1600 gamma[3] -0.057 4.404 -8.473 -2.878 -0.165 2.552 9.101 1.002 1200 gamma[4] -1.703 4.521 -10.015 -4.635 -1.863 1.037 7.951 1.002 1100 gamma[5] -0.476 4.479 -8.892 -3.343 -0.596 2.264 8.743 1.001 2400 gamma[6] 3.756 4.639 -5.926 0.900 3.928 6.736 12.630 1.002 2100 gamma[7] 5.604 4.990 -4.898 2.573 5.861 8.939 14.660 1.002 1500 gamma[8] -1.797 4.505 -10.125 -4.771 -1.947 0.878 8.022 1.002 1700 sd.Leaf 3.798 1.820 0.412 2.604 3.849 4.884 7.482 1.002 2900 sd.Resid 4.304 0.934 2.972 3.595 4.154 4.894 6.480 1.001 2900 sd.Treatment 5.534 1.656 2.253 4.484 5.497 6.547 8.997 1.004 1000 sigma.leaf 4.599 2.747 0.444 2.812 4.221 5.832 11.175 1.001 2900 sigma.res 4.669 1.364 2.674 3.661 4.452 5.428 7.948 1.001 2900 deviance 92.603 6.931 80.944 87.315 92.201 97.366 106.748 1.001 2900 For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1). DIC info (using the rule, pD = var(deviance)/2) pD = 24.0 and DIC = 116.6 DIC is an estimate of expected predictive error (lower deviance is better).tobacco.mcmc.b <- tobacco.r2jags.b$BUGSoutput$sims.matrix
Matrix parameterization STAN coderstanString=" data{ int n; int nZ; int nX; vector [n] y; matrix [n,nX] X; matrix [n,nZ] Z; vector [nX] a0; matrix [nX,nX] A0; } parameters{ vector [nX] beta; real<lower=0> sigma; vector [nZ] gamma; real<lower=0> sigma_Z; } transformed parameters { vector [n] mu; mu <- Z*gamma + X*beta; } model{ // Priors beta ~ multi_normal(a0,A0); gamma ~ normal( 0 , sigma_Z ); sigma_Z ~ cauchy(0,25); sigma ~ cauchy(0,25); y ~ normal( mu , sigma ); } generated quantities { vector [n] y_err; real<lower=0> sd_Resid; y_err <- y - mu; sd_Resid <- sd(y_err); } " # Generate a data list Xmat <- model.matrix(~TREATMENT, data=tobacco) Zmat <- model.matrix(~-1+LEAF, data=tobacco) tobacco.list <- with(tobacco, list(y=NUMBER, Z=Zmat, X=Xmat, nX=ncol(Xmat), nZ=ncol(Zmat), n=nrow(tobacco), a0=rep(0,ncol(Xmat)), A0=diag(100000,ncol(Xmat)) ) ) # define parameters burnInSteps = 6000 nChains = 3 numSavedSteps = 3000 thinSteps = 100 nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) library(rstan) tobacco.rstan.a <- stan(data=tobacco.list, model_code=rstanString, pars=c('beta','gamma','sigma','sigma_Z', 'sd_Resid'), chains=nChains, iter=nIter, warmup=burnInSteps, thin=thinSteps, save_dso=TRUE )
TRANSLATING MODEL 'rstanString' FROM Stan CODE TO C++ CODE NOW. COMPILING THE C++ CODE FOR MODEL 'rstanString' NOW. SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 1). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.4 seconds (Warm-up) # 30.66 seconds (Sampling) # 31.06 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 2). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.45 seconds (Warm-up) # 10.61 seconds (Sampling) # 11.06 seconds (Total) SAMPLING FOR MODEL 'rstanString' NOW (CHAIN 3). Iteration: 1 / 106000 [ 0%] (Warmup) Iteration: 6001 / 106000 [ 5%] (Sampling) Iteration: 16600 / 106000 [ 15%] (Sampling) Iteration: 27200 / 106000 [ 25%] (Sampling) Iteration: 37800 / 106000 [ 35%] (Sampling) Iteration: 48400 / 106000 [ 45%] (Sampling) Iteration: 59000 / 106000 [ 55%] (Sampling) Iteration: 69600 / 106000 [ 65%] (Sampling) Iteration: 80200 / 106000 [ 75%] (Sampling) Iteration: 90800 / 106000 [ 85%] (Sampling) Iteration: 101400 / 106000 [ 95%] (Sampling) Iteration: 106000 / 106000 [100%] (Sampling) # Elapsed Time: 0.51 seconds (Warm-up) # 9.81 seconds (Sampling) # 10.32 seconds (Total)
print(tobacco.rstan.a)
Inference for Stan model: rstanString. 3 chains, each with iter=106000; warmup=6000; thin=100; post-warmup draws per chain=1000, total post-warmup draws=3000. mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat beta[1] 34.92 0.04 2.36 30.28 33.54 34.93 36.37 39.72 3000 1 beta[2] -7.89 0.04 2.40 -12.76 -9.34 -7.87 -6.45 -3.00 3000 1 gamma[1] -0.26 0.05 2.68 -5.95 -1.79 -0.24 1.24 5.09 2656 1 gamma[2] -1.28 0.05 2.77 -7.01 -2.95 -1.09 0.41 4.00 3000 1 gamma[3] -0.61 0.05 2.73 -6.47 -2.16 -0.48 0.99 4.85 3000 1 gamma[4] -2.10 0.06 2.91 -8.26 -3.95 -1.84 -0.14 3.26 2772 1 gamma[5] -1.01 0.05 2.75 -6.80 -2.58 -0.89 0.60 4.42 3000 1 gamma[6] 2.92 0.06 3.11 -2.30 0.65 2.54 4.93 9.57 3000 1 gamma[7] 4.61 0.07 3.62 -1.08 1.77 4.40 7.03 12.33 3000 1 gamma[8] -2.23 0.05 2.83 -8.28 -3.93 -1.92 -0.26 2.84 2938 1 sigma 4.65 0.03 1.32 2.67 3.68 4.46 5.40 7.72 2675 1 sigma_Z 4.04 0.04 2.34 0.54 2.48 3.76 5.15 9.45 3000 1 sd_Resid 4.26 0.02 0.84 2.98 3.60 4.14 4.87 5.98 2769 1 lp__ -42.06 0.08 4.10 -50.09 -44.41 -41.98 -39.80 -32.84 2574 1 Samples were drawn using NUTS(diag_e) at Fri Jan 30 11:30:36 2015. For each parameter, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).tobacco.mcmc.d <- rstan:::as.mcmc.list.stanfit(tobacco.rstan.a) tobacco.mcmc.df.d <- as.data.frame(extract(tobacco.rstan.a))
library(plyr) #Finite-population standard deviations ## Leaf library(coda) sd.leaf <- tobacco.mcmc.df.d[,3:10] SD.leaf <- apply(sd.leaf,1,sd) data.frame(mean=mean(SD.leaf), median=median(SD.leaf), HPDinterval(as.mcmc(SD.leaf)), HPDinterval(as.mcmc(SD.leaf),p=0.68))
mean median lower upper lower.1 upper.1 var1 3.288 3.385 0.364 5.676 1.891 4.835
#Treatment treatments <- NULL treatments <- cbind(tobacco.mcmc.df.d[,'beta.1'], tobacco.mcmc.df.d[,'beta.1']+tobacco.mcmc.df.d[,'beta.2']) sd.treatment <- apply(treatments,1,sd) data.frame(mean=mean(sd.treatment), median=median(sd.treatment), HPDinterval(as.mcmc(sd.treatment)), HPDinterval(as.mcmc(sd.treatment),p=0.68))
mean median lower upper lower.1 upper.1 var1 5.587 5.565 2.288 9.159 3.965 7.02
- Full Effects parameterization - random intercepts model (JAGS)
- Before fully exploring the parameters, it is prudent to examine the convergence and mixing diagnostics.
Chose either any of the parameterizations (they should yield much the same) - although it is sometimes useful to explore the
different performances of effects vs matrix and JAGS vs STAN.
Full effects parameterization JAGS code
library(coda) plot(as.mcmc(tobacco.r2jags.a))
Error: invalid 'length' argument
preds <- c("beta.leaf[1]","beta.treatment[2]", "sigma.res", "sigma.leaf") autocorr.diag(as.mcmc(tobacco.r2jags.a)[, preds])
Error: incorrect number of dimensions
raftery.diag(as.mcmc(tobacco.r2jags.a))
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Matrix parameterization JAGS codelibrary(coda) plot(as.mcmc(tobacco.r2jags.b))
Error: invalid 'length' argument
preds <- c("beta[1]","beta[2]", "sigma.res", "sigma.leaf") autocorr.diag(as.mcmc(tobacco.r2jags.b)[, preds])
Error: incorrect number of dimensions
raftery.diag(as.mcmc(tobacco.r2jags.b))
Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
Matrix parameterization STAN codelibrary(coda) preds <- c("beta[1]", "beta[2]", "sigma", "sigma_Z") plot(tobacco.mcmc.d)




autocorr.diag(tobacco.mcmc.d[, preds])
beta[1] beta[2] sigma sigma_Z Lag 0 1.000000 1.000000 1.00000 1.000000 Lag 100 -0.018868 -0.006011 0.03265 -0.002893 Lag 500 -0.005449 0.005173 -0.02275 -0.018524 Lag 1000 -0.007707 0.017508 -0.04330 0.022630 Lag 5000 -0.011061 0.019536 0.00145 0.007100
raftery.diag(tobacco.mcmc.d)
[[1]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[2]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s [[3]] Quantile (q) = 0.025 Accuracy (r) = +/- 0.005 Probability (s) = 0.95 You need a sample size of at least 3746 with these values of q, r and s
- Summary figure time
Matrix parameterization JAGS code
preds <- c('beta[1]','beta[2]') coefs <- tobacco.r2jags.b$BUGSoutput$sims.matrix[,preds] newdata <- data.frame(TREAT=levels(tobacco$TREAT)) Xmat <- model.matrix(~TREAT, newdata) pred <- coefs %*% t(Xmat) library(plyr) newdata <- cbind(newdata, adply(pred, 2, function(x) { data.frame(Median=median(x), HPDinterval(as.mcmc(x)), HPDinterval(as.mcmc(x), p=0.68)) })) newdata
TREAT X1 Median lower upper lower.1 upper.1 1 Strong 1 33.59 14.040 50.36 25.63 42.90 2 Weak 2 25.90 5.961 42.52 17.06 34.29
library(ggplot2) p1 <- ggplot(newdata, aes(y=Median, x=TREAT)) + geom_linerange(aes(ymin=lower, ymax=upper), show_guide=FALSE)+ geom_linerange(aes(ymin=lower.1, ymax=upper.1), size=2,show_guide=FALSE)+ geom_point(size=4, shape=21, fill="white")+ scale_y_continuous('Number of lessions')+ theme_classic()+ theme(axis.title.y=element_text(vjust=2,size=rel(1.2)), axis.title.x=element_text(vjust=-2,size=rel(1.2)), plot.margin=unit(c(0.5,0.5,2,2), 'lines')) preds <- c('sd.Resid','sd.Treatment','sd.Leaf') tobacco.sd <- adply(tobacco.mcmc.b[,preds],2,function(x) { data.frame(mean=mean(x), median=median(x), HPDinterval(as.mcmc(x)), HPDinterval(as.mcmc(x),p=0.68)) }) head(tobacco.sd)
X1 mean median lower upper lower.1 upper.1 1 sd.Resid 4.304 4.154 2.785436 6.061 3.105 4.837 2 sd.Treatment 5.534 5.497 2.149849 8.824 4.020 7.137 3 sd.Leaf 3.798 3.849 0.005277 6.582 2.198 5.537
rownames(tobacco.sd) <- c("Residuals", "Treatment", "Leaf") tobacco.sd$name <- factor(c("Residuals", "Treatment", "Leaf"), levels=c("Residuals", "Treatment", "Leaf")) tobacco.sd$Perc <- tobacco.sd$median/sum(tobacco.sd$median) p2<-ggplot(tobacco.sd,aes(y=name, x=median))+ geom_vline(xintercept=0,linetype="dashed")+ geom_hline(xintercept=0)+ scale_x_continuous("Finite population \nvariance components (sd)")+ geom_errorbarh(aes(xmin=lower.1, xmax=upper.1), height=0, size=1)+ geom_errorbarh(aes(xmin=lower, xmax=upper), height=0, size=1.5)+ geom_point(size=3, shape=21, fill='white')+ geom_text(aes(label=sprintf("(%4.1f%%)",Perc),vjust=-1))+ theme_classic()+ theme(axis.title.y=element_blank(), axis.text.y=element_text(size=rel(1.2),hjust=1)) library(gridExtra) grid.arrange(p1,p2,ncol=2)

