Tutorial 9.9b - Split-plot ANOVA (Bayesian)
14 Jan 2014
If you are completely ontop of the conceptual issues pertaining to Randomized Complete Block (RCB) ANOVA, and just need to use this tutorial in order to learn about RCB ANOVA in R, you are invited to skip down to the section on RCB ANOVA in R.
Overview
You are strongly advised to review the information on the nested design in tutorial 9.9a. I am not going to duplicate the overview here.
Split-plot ANOVA in R
Scenario and Data
Imagine we has designed an experiment in which we intend to measure a response ($y$) to one of treatments (three levels; 'a1', 'a2' and 'a3'). Unfortunately, the system that we intend to sample is spatially heterogeneous and thus will add a great deal of noise to the data that will make it difficult to detect a signal (impact of treatment).
Thus in an attempt to constrain this variability you decide to apply a design (RCB) in which each of the treatments within each of 35 blocks dispersed randomly throughout the landscape. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the number of between block treatments (A) = 3
- the number of blocks = 35
- the number of within block treatments (C) = 3
- the mean of the treatments = 40, 70 and 80 respectively
- the variability (standard deviation) between blocks of the same treatment = 12
- the variability (standard deviation) between treatments withing blocks = 5
> library(plyr) > set.seed(1) > nA <- 3 > nC <- 3 > nBlock <- 35 > sigma <- 5 > sigma.block <- 12 > n <- nBlock * nC > Block <- gl(nBlock, k = 1) > C <- gl(nC, k = 1) > > ## Specify the cell means > AC.means <- (rbind(c(40, 70, 80), c(35, 50, 70), c(35, 40, 45))) > ## Convert these to effects > X <- model.matrix(~A * C, data = expand.grid(A = gl(3, k = 1), C = gl(3, k = 1))) > AC <- as.vector(AC.means) > AC.effects <- solve(X, AC) > > A <- gl(nA, nBlock, n) > dt <- expand.grid(C = C, Block = Block) > dt <- data.frame(dt, A) > > Xmat <- cbind(model.matrix(~-1 + Block, data = dt), model.matrix(~A * C, data = dt)) > block.effects <- rnorm(n = nBlock, mean = 0, sd = sigma.block) > all.effects <- c(block.effects, AC.effects) > lin.pred <- Xmat %*% all.effects > > ## the quadrat observations (within sites) are drawn from normal distributions with means according to > ## the site means and standard deviations of 5 > y <- rnorm(n, lin.pred, sigma) > data <- data.frame(y = y, A = A, dt) > head(data) #print out the first six rows of the data set
y A C Block A.1 1 30.41 1 1 1 1 2 60.51 1 2 1 1 3 72.19 1 3 1 1 4 47.70 1 1 2 1 5 76.02 1 2 2 1 6 81.38 1 3 2 1
> tapply(data$y, data$A, mean)
1 2 3 67.22 53.30 37.83
> tapply(data$y, data$C, mean)
1 2 3 37.01 54.34 67.01
> > library(car) > with(data, interaction.plot(C, A, y))
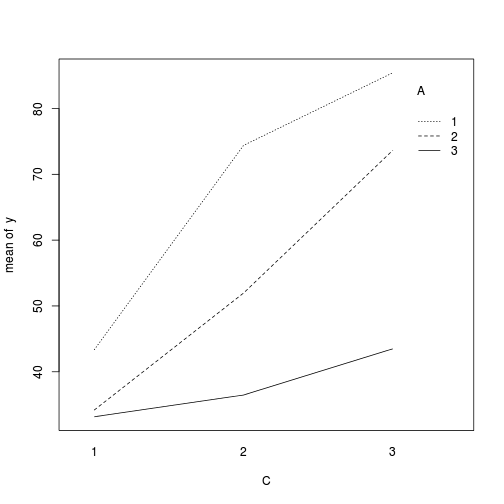
> library(ggplot2) > ggplot(data, aes(y = y, x = C, color = A)) + geom_point() + facet_wrap(~Block)
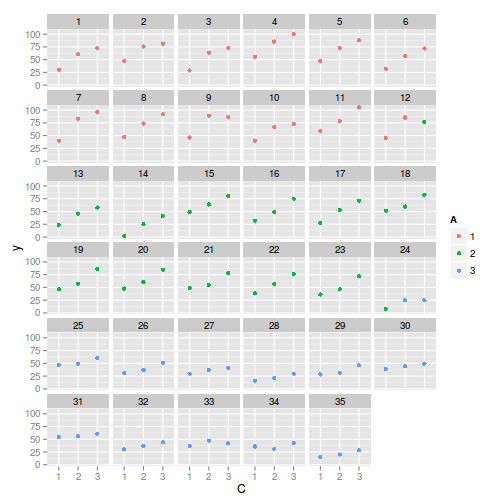
> > library(nlme) > summary(lme(y ~ A * C, random = ~1 | Block, data))
Linear mixed-effects model fit by REML
Data: data
AIC BIC logLik
693.6 721.8 -335.8
Random effects:
Formula: ~1 | Block
(Intercept) Residual
StdDev: 11.38 4.205
Fixed effects: y ~ A * C
Value Std.Error DF t-value p-value
(Intercept) 43.12 3.125 62 13.800 0.0000
A2 -10.30 3.737 62 -2.756 0.0077
A3 -8.23 4.350 62 -1.891 0.0632
C2 31.05 1.717 62 18.086 0.0000
C3 42.66 1.770 62 24.100 0.0000
A2:C2 -15.19 2.471 62 -6.149 0.0000
A3:C2 -26.25 2.466 62 -10.646 0.0000
A2:C3 -5.39 2.504 62 -2.152 0.0353
A3:C3 -30.84 2.504 62 -12.314 0.0000
Correlation:
(Intr) A2 A3 C2 C3 A2:C2 A3:C2 A2:C3
A2 -0.666
A3 -0.677 0.585
C2 -0.275 0.230 0.197
C3 -0.238 0.179 0.166 0.485
A2:C2 0.202 -0.304 -0.178 -0.695 -0.338
A3:C2 0.196 -0.147 -0.311 -0.696 -0.338 0.480
A2:C3 0.227 -0.340 -0.199 -0.343 -0.714 0.488 0.234
A3:C3 0.173 -0.114 -0.288 -0.343 -0.707 0.235 0.508 0.500
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-1.90154 -0.53579 -0.04229 0.58817 2.08273
Number of Observations: 105
Number of Groups: 35
JAGS
| Full parameterization | Matrix parameterization | Heirarchical parameterization |
|---|---|---|
| $$ \begin{array}{rcl} y_{ijk}&\sim&\mathcal{N}(\mu_{ij},\sigma^2)\\ \mu_{ij} &=& \alpha_0 + \alpha_{i} + \beta_{j} + \gamma_{k} + \alpha\gamma\\ \beta_{i{j}}&\sim&\mathcal{N}(0,\sigma_{B}^2)\\ \alpha_0, \alpha_i&\sim&\mathcal{N}(0,100000)\\ \sigma^2&\sim&\mathcal{U}(0,100)\\ \sigma_{B}^2&\sim&\mathcal{U}(0,100)\\ \end{array} $$ | $$ \begin{array}{rcl} y_{ijk}&\sim&\mathcal{N}(\mu_{ij},\sigma^2)\\ \mu_{ij} &=& \alpha\mathbf{X} + \beta_{j(i)}\\ \beta_{i{j}}&\sim&\mathcal{N}(0,\sigma_{B}^2)\\ \alpha&\sim&\mathcal{MVN}(0,100000)\\ \sigma^2&\sim&\mathcal{U}(0,100)\\ \sigma_{B}^2&\sim&\mathcal{U}(0,100)\\ \end{array} $$ | $$ \begin{array}{rcl} y_{ij}&\sim &\mathcal{N}(\beta_{j(i)}, \sigma^2)\\ \beta_{j(i)}&\sim&\mathcal{N}(\mu_{i},\sigma_{B}^2)\\ \mu_{i}&=&\alpha\mathbf{X}\\ \alpha_i&\sim&\mathcal{N}(0, 1000000)\\ \sigma^2&\sim&\mathcal{U}(0,100)\\ \sigma_{B}^2&\sim&\mathcal{U}(0,100) \end{array} $$ |
Full effects parameterization
> modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha0 + alpha[A[i]]+beta[Block[i]] + C.gamma[C[i]] + AC.gamma[A[i],C[i]] } #Priors alpha0 ~ dnorm(0, 1.0E-6) alpha[1] <- 0 for (i in 2:nA) { alpha[i] ~ dnorm(0, 1.0E-6) #prior AC.gamma[i,1] <- 0 } for (i in 1:nBlock) { beta[i] ~ dnorm(0, tau.B) #prior } C.gamma[1] <- 0 for (i in 2:nC) { C.gamma[i] ~ dnorm(0, 1.0E-6) AC.gamma[1,i] <- 0 } AC.gamma[1,1] <- 0 for (i in 2:nA) { for (j in 2:nC) { AC.gamma[i,j] ~ dnorm(0, 1.0E-6) } } sigma ~ dunif(0, 100) tau <- 1 / (sigma * sigma) sigma.B ~ dunif(0, 100) tau.B <- 1 / (sigma.B * sigma.B) } " > writeLines(modelString,con="../downloads/BUGSscripts/tut9.9jagsF.txt")
> data.list <- with(data, + list(y=y, + Block=as.numeric(Block), + A=as.numeric(A), + C=as.numeric(C), + n=nrow(data), + nA = length(levels(A)), + nC = length(levels(C)), + nBlock = length(levels(Block)) + ) + ) > > params <- c("alpha0","alpha",'C.gamma','AC.gamma',"sigma","sigma.B") > adaptSteps = 1000 > burnInSteps = 3000 > nChains = 3 > numSavedSteps = 3000 > thinSteps = 10 > nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) > > library(R2jags) > rnorm(1)
[1] 0.06851
> jags.f.time <- system.time( + data.r2jags.f <- jags(data=data.list, + inits=NULL, + parameters.to.save=params, + model.file="../downloads/BUGSscripts/tut9.9jagsF.txt", + n.chains=3, + n.iter=nIter, + n.burnin=burnInSteps, + n.thin=thinSteps + ) + )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 590 Initializing model
> print(data.r2jags.f)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.9jagsF.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
AC.gamma[1,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
AC.gamma[2,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
AC.gamma[3,1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
AC.gamma[1,2] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
AC.gamma[2,2] -15.198 2.598 -20.378 -16.936 -15.181 -13.435 -10.239 1.002 1400
AC.gamma[3,2] -26.240 2.537 -31.344 -27.946 -26.266 -24.511 -21.176 1.001 3000
AC.gamma[1,3] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
AC.gamma[2,3] -5.288 2.551 -10.302 -6.998 -5.301 -3.593 -0.259 1.002 1500
AC.gamma[3,3] -30.834 2.533 -35.739 -32.506 -30.807 -29.130 -25.838 1.001 2200
C.gamma[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
C.gamma[2] 31.042 1.787 27.516 29.889 31.042 32.182 34.548 1.001 2200
C.gamma[3] 42.639 1.811 38.952 41.454 42.662 43.827 46.112 1.001 2200
alpha[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
alpha[2] -10.369 3.826 -18.042 -12.941 -10.364 -7.712 -3.162 1.001 3000
alpha[3] -8.196 4.518 -16.968 -11.325 -8.170 -5.159 0.453 1.001 3000
alpha0 43.090 3.227 36.783 40.963 43.004 45.206 49.306 1.001 3000
sigma 4.304 0.399 3.625 4.012 4.269 4.566 5.177 1.001 3000
sigma.B 11.818 1.676 9.095 10.646 11.666 12.783 15.610 1.002 1400
deviance 602.341 12.484 580.617 593.546 601.417 610.192 628.544 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 78.0 and DIC = 680.3
DIC is an estimate of expected predictive error (lower deviance is better).
> data.mcmc.list.f <- as.mcmc(data.r2jags.f)
[1] "AC.gamma[1,1]" "AC.gamma[2,1]" "AC.gamma[3,1]" "AC.gamma[1,2]" "AC.gamma[2,2]" "AC.gamma[3,2]" "AC.gamma[1,3]" "AC.gamma[2,3]" "AC.gamma[3,3]" "C.gamma[1]" "C.gamma[2]" "C.gamma[3]" [13] "alpha[1]" "alpha[2]" "alpha[3]" "alpha0" "deviance" "sigma" "sigma.B"
JAGS Full [1,] "13000" [2,] "10" [3,] "3000" [4,] "0.0181" [5,] "43.00 [36.57 , 49.04]" [6,] "-10.36 [-17.73 , -2.89]" [7,] "-8.17 [-16.63 , 0.69]" [8,] "31.04 [27.40 , 34.35]" [9,] "42.66 [38.89 , 46.00]" [10,] "-15.18 [-20.11 , -10.07]" [11,] "-26.27 [-31.15 , -21.10]" [12,] "-5.30 [-10.10 , -0.16]" [13,] "-30.81 [-35.70 , -25.79]" [14,] "4.27 [3.60 , 5.11]" [15,] "11.67 [8.77 , 15.24]" [16,] "4.06" [17,] "0.00" [18,] "4.07" [19,] "0.00" [20,] "0.00"
Matrix parameterization
> modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- beta[Block[i]] + inprod(alpha[],X[i,]) } #Priors alpha ~ dmnorm(a0,A0) for (i in 1:nBlock) { beta[i] ~ dnorm(0, tau.B) #prior } sigma ~ dunif(0, 100) tau <- 1 / (sigma * sigma) sigma.B ~ dunif(0, 100) tau.B <- 1 / (sigma.B * sigma.B) } " > writeLines(modelString,con="../downloads/BUGSscripts/tut9.9jagsM.txt")
> Xmat <- model.matrix(~A*C,data) > nX <- ncol(Xmat) > data.list <- with(data, + list(y=y, + Block=as.numeric(Block), + X=Xmat, + n=nrow(data), + nBlock=length(levels(Block)), + a0=rep(0,nX), A0=diag(1.0E-06,nX) + ) + ) > > params <- c("alpha","sigma","sigma.B") > adaptSteps = 1000 > burnInSteps = 3000 > nChains = 3 > numSavedSteps = 3000 > thinSteps = 10 > nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) > > library(R2jags) > rnorm(1)
[1] 0.101
> jags.m.time <- system.time( + data.r2jags.m <- jags(data=data.list, + inits=NULL, + parameters.to.save=params, + model.file="../downloads/BUGSscripts/tut9.9jagsM.txt", + n.chains=3, + n.iter=nIter, + n.burnin=burnInSteps, + n.thin=thinSteps + ) + )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 1513 Initializing model
> print(data.r2jags.m)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.9jagsM.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 43.069 3.217 36.797 40.915 43.072 45.253 49.439 1.001 3000
alpha[2] -10.187 3.861 -17.580 -12.803 -10.170 -7.557 -2.642 1.001 2900
alpha[3] -8.101 4.546 -16.833 -11.200 -8.212 -5.130 0.926 1.001 3000
alpha[4] 31.027 1.762 27.606 29.873 31.017 32.196 34.452 1.001 2300
alpha[5] 42.644 1.825 39.093 41.414 42.646 43.820 46.266 1.001 3000
alpha[6] -15.207 2.511 -20.188 -16.946 -15.220 -13.513 -10.298 1.002 1500
alpha[7] -26.162 2.547 -31.240 -27.837 -26.181 -24.472 -21.105 1.001 3000
alpha[8] -5.403 2.560 -10.371 -7.110 -5.453 -3.779 -0.250 1.001 3000
alpha[9] -30.753 2.570 -35.819 -32.463 -30.768 -29.051 -25.649 1.001 3000
sigma 4.295 0.398 3.608 4.003 4.265 4.546 5.140 1.001 3000
sigma.B 11.829 1.646 9.103 10.673 11.639 12.841 15.505 1.002 2000
deviance 602.069 12.546 580.515 593.034 601.185 609.968 629.064 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 78.7 and DIC = 680.8
DIC is an estimate of expected predictive error (lower deviance is better).
> data.mcmc.list.m <- as.mcmc(data.r2jags.m) > Data.mcmc.list.m <- data.mcmc.list.m
JAGS Full JAGS Matrix [1,] "13000" "13000" [2,] "10" "10" [3,] "3000" "3000" [4,] "0.0181" "0.0315" [5,] "43.00 [36.57 , 49.04]" "43.07 [36.99 , 49.48]" [6,] "-10.36 [-17.73 , -2.89]" "-10.17 [-17.60 , -2.69]" [7,] "-8.17 [-16.63 , 0.69]" "-8.21 [-17.27 , 0.37]" [8,] "31.04 [27.40 , 34.35]" "31.02 [27.57 , 34.38]" [9,] "42.66 [38.89 , 46.00]" "42.65 [39.08 , 46.25]" [10,] "-15.18 [-20.11 , -10.07]" "-15.22 [-20.17 , -10.28]" [11,] "-26.27 [-31.15 , -21.10]" "-26.18 [-31.22 , -21.09]" [12,] "-5.30 [-10.10 , -0.16]" "-5.45 [-10.70 , -0.61]" [13,] "-30.81 [-35.70 , -25.79]" "-30.77 [-35.70 , -25.62]" [14,] "4.27 [3.60 , 5.11]" "4.27 [3.60 , 5.11]" [15,] "11.67 [8.77 , 15.24]" "11.64 [8.91 , 15.18]" [16,] "4.06" "5.45" [17,] "0.00" "0.00" [18,] "4.07" "5.48" [19,] "0.00" "0.00" [20,] "0.00" "0.00"
Split-plot (repeated measures) ANOVA in R
Scenario and Data
Imagine we has designed an experiment in which we intend to measure a response ($y$) to one of treatments (three levels; 'a1', 'a2' and 'a3'). Unfortunately, the system that we intend to sample is spatially heterogeneous and thus will add a great deal of noise to the data that will make it difficult to detect a signal (impact of treatment).
Thus in an attempt to constrain this variability you decide to apply a design (RCB) in which each of the treatments within each of 35 blocks dispersed randomly throughout the landscape. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the number of between block treatments (A) = 3
- the number of blocks = 35
- the number of within block treatments (C) = 3
- the mean of the treatments = 40, 70 and 80 respectively
- the variability (standard deviation) between blocks of the same treatment = 12
- the variability (standard deviation) between treatments withing blocks = 5
> library(plyr) > set.seed(1) > nA <- 3 > nC <- 10 > nBlock <- 35 > sigma <- 50 > sigma.block <- 30 > n <- nBlock*nC > Block <- gl(nBlock, k=1) > C <- 1:10 > > ## Specify the cell means > intercepts <- c(200,170,160) > slopes <- c(30,10,0) > AC.effects<-c(intercepts[1], #intercept + as.vector(outer(intercepts[-1],intercepts[1],'-')), # A effects + slopes[1], + as.vector(outer(slopes[-1],slopes[1],'-')) # Slope effects + ) > > A <- gl(nA,nC,n) > dt <- expand.grid(C=C,Block=Block) > dt <- data.frame(dt,A) > > Xmat <- cbind(model.matrix(~-1+Block, data=dt),model.matrix(~A*C, data=dt)) > block.effects <- rnorm(n = nBlock, mean =0 , sd = sigma.block) > all.effects <- c(block.effects, AC.effects) > lin.pred <- Xmat %*% all.effects > > ## the quadrat observations (within sites) are drawn from > ## normal distributions with means according to the site means > ## and standard deviations of 5 > y <- rnorm(n,lin.pred,sigma) > data <- data.frame(y=y, A=A,dt) > head(data) #print out the first six rows of the data set
y A C Block A.1 1 190.5 1 1 1 1 2 221.5 1 2 1 1 3 268.2 1 3 1 1 4 356.2 1 4 1 1 5 369.4 1 5 1 1 6 353.0 1 6 1 1
> > library(car) > with(data,interaction.plot(C,A,y))
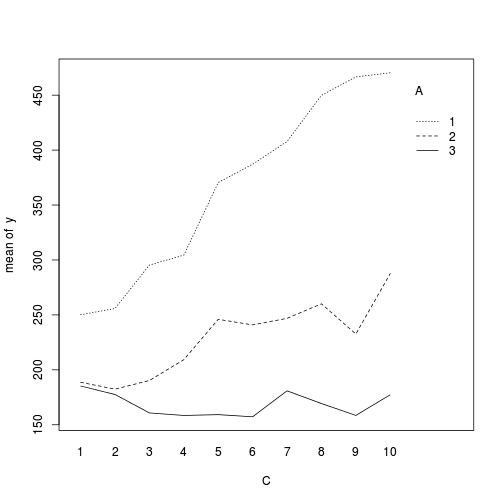
> library(ggplot2) > ggplot(data, aes(y=y, x=C,color=A)) + geom_point() + geom_smooth(method='lm') + + facet_wrap(~Block)
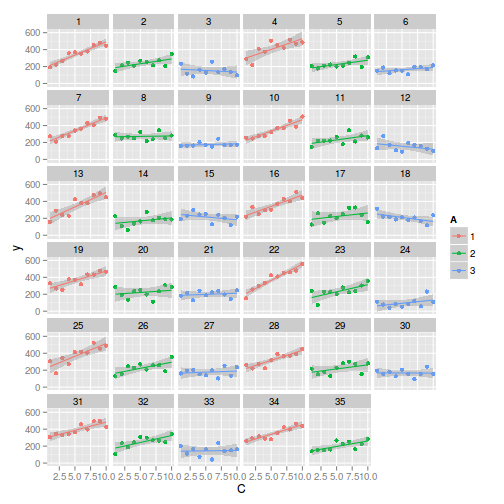
> > library(nlme) > summary(lme(y~A*C, random=~1|Block, data))
Linear mixed-effects model fit by REML
Data: data
AIC BIC logLik
3731 3762 -1858
Random effects:
Formula: ~1 | Block
(Intercept) Residual
StdDev: 22.5 48.27
Fixed effects: y ~ A * C
Value Std.Error DF t-value p-value
(Intercept) 213.95 11.524 312 18.567 0.0000
A2 -42.09 16.297 32 -2.583 0.0146
A3 -42.22 16.663 32 -2.534 0.0164
C 27.62 1.534 312 18.004 0.0000
A2:C -17.32 2.169 312 -7.983 0.0000
A3:C -28.21 2.218 312 -12.717 0.0000
Correlation:
(Intr) A2 A3 C A2:C
A2 -0.707
A3 -0.692 0.489
C -0.732 0.518 0.506
A2:C 0.518 -0.732 -0.358 -0.707
A3:C 0.506 -0.358 -0.732 -0.692 0.489
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.64777 -0.63846 -0.03841 0.63465 2.50709
Number of Observations: 350
Number of Groups: 35
JAGS
| Full parameterization | Matrix parameterization | Heirarchical parameterization |
|---|---|---|
| $$ \begin{array}{rcl} y_{ijk}&\sim&\mathcal{N}(\mu_{ij},\sigma^2)\\ \mu_{ij} &=& \beta_{j} + \alpha_0 + \alpha_{i} + \\ \beta_{i{j}}&\sim&\mathcal{N}(0,\sigma_{B}^2)\\ \alpha_0, \alpha_i&\sim&\mathcal{N}(0,100000)\\ \sigma^2&\sim&\mathcal{U}(0,100)\\ \sigma_{B}^2&\sim&\mathcal{U}(0,100)\\ \end{array} $$ | $$ \begin{array}{rcl} y_{ijk}&\sim&\mathcal{N}(\mu_{ij},\sigma^2)\\ \mu_{ij} &=& \alpha\mathbf{X} + \beta_{j(i)}\\ \beta_{i{j}}&\sim&\mathcal{N}(0,\sigma_{B}^2)\\ \alpha&\sim&\mathcal{MVN}(0,100000)\\ \sigma^2&\sim&\mathcal{U}(0,100)\\ \sigma_{B}^2&\sim&\mathcal{U}(0,100)\\ \end{array} $$ | $$ \begin{array}{rcl} y_{ij}&\sim &\mathcal{N}(\beta_{j(i)}, \sigma^2)\\ \beta_{j(i)}&\sim&\mathcal{N}(\mu_{i},\sigma_{B}^2)\\ \mu_{i}&=&\alpha\mathbf{X}\\ \alpha_i&\sim&\mathcal{N}(0, 1000000)\\ \sigma^2&\sim&\mathcal{U}(0,100)\\ \sigma_{B}^2&\sim&\mathcal{U}(0,100) \end{array} $$ |
Full effects parameterization
> modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- alpha0 + alpha1[A[i]] + beta[Block[i]] + C.gamma*C[i] + AC.gamma[A[i]]*C[i] } #Priors alpha0 ~ dnorm(0, 1.0E-6) alpha1[1] <- 0 AC.gamma[1] <- 0 for (i in 2:nA) { alpha1[i] ~ dnorm(0, 1.0E-06) #prior AC.gamma[i] ~ dnorm(0, 1.0E-06) #prior } for (i in 1:nBlock) { beta[i] ~ dnorm(0, tau.B) #prior } C.gamma ~ dnorm(0, 1.0E-06) #prior sigma ~ dunif(0, 100) tau <- 1 / (sigma * sigma) sigma.B ~ dunif(0, 100) tau.B <- 1 / (sigma.B * sigma.B) } " > writeLines(modelString,con="../downloads/BUGSscripts/tut9.9jagsF.T.txt")
> data.list <- with(data, + list(y=y, + A=as.numeric(A), + Block=as.numeric(Block), + C=C, + n=nrow(data), + nA=length(levels(A)), + nBlock = length(levels(Block)) + ) + ) > > params <- c("alpha0","alpha1",'C.gamma','AC.gamma',"sigma","sigma.B") > adaptSteps = 1000 > burnInSteps = 3000 > nChains = 3 > numSavedSteps = 3000 > thinSteps = 10 > nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) > > library(R2jags) > rnorm(1)
[1] 0.9164
> jags.f.T.time <- system.time( + data.r2jags.f.T <- jags(data=data.list, + inits=NULL, + parameters.to.save=params, + model.file="../downloads/BUGSscripts/tut9.9jagsF.T.txt", + n.chains=3, + n.iter=nIter, + n.burnin=burnInSteps, + n.thin=thinSteps + ) + )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 1846 Initializing model
> print(data.r2jags.f.T)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.9jagsF.T.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
AC.gamma[1] 0.00 0.000 0.00 0.00 0.00 0.00 0.000 1.000 1
AC.gamma[2] -17.30 2.166 -21.54 -18.81 -17.25 -15.86 -13.065 1.001 3000
AC.gamma[3] -28.20 2.238 -32.58 -29.68 -28.19 -26.71 -23.743 1.001 3000
C.gamma 27.61 1.528 24.62 26.59 27.57 28.68 30.580 1.002 1900
alpha0 214.10 11.794 191.39 206.33 213.87 222.14 237.412 1.002 1400
alpha1[1] 0.00 0.000 0.00 0.00 0.00 0.00 0.000 1.000 1
alpha1[2] -42.36 16.683 -74.79 -53.54 -42.49 -31.20 -8.608 1.001 2200
alpha1[3] -42.26 16.993 -75.50 -53.61 -42.24 -30.82 -8.983 1.001 3000
sigma 48.46 1.950 44.93 47.13 48.38 49.76 52.554 1.002 1000
sigma.B 23.26 4.407 15.50 20.11 22.94 25.95 32.747 1.001 3000
deviance 3708.75 9.704 3692.31 3701.63 3707.86 3714.89 3730.145 1.002 1600
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 47.1 and DIC = 3755.8
DIC is an estimate of expected predictive error (lower deviance is better).
> data.mcmc.list.f.T <- as.mcmc(data.r2jags.f.T)
[1] "AC.gamma[1]" "AC.gamma[2]" "AC.gamma[3]" "C.gamma" "alpha0" "alpha1[1]" "alpha1[2]" "alpha1[3]" "deviance" "sigma" "sigma.B"
Error: obj must have nsamp > 1
NULL
Matrix parameterization
> modelString=" model { #Likelihood for (i in 1:n) { y[i]~dnorm(mu[i],tau) mu[i] <- beta[Block[i]] + inprod(alpha[],X[i,]) } #Priors alpha ~ dmnorm(a0,A0) for (i in 1:nBlock) { beta[i] ~ dnorm(0, tau.B) #prior } sigma ~ dunif(0, 100) tau <- 1 / (sigma * sigma) sigma.B ~ dunif(0, 100) tau.B <- 1 / (sigma.B * sigma.B) } " > writeLines(modelString,con="../downloads/BUGSscripts/tut9.9jagsM.T.txt")
> Xmat <- model.matrix(~A*C,data) > nX <- ncol(Xmat) > data.list <- with(data, + list(y=y, + Block=as.numeric(Block), + X=Xmat, + n=nrow(data), + nBlock=length(levels(Block)), + a0=rep(0,nX), A0=diag(1.0E-06,nX) + ) + ) > > params <- c("alpha","sigma","sigma.B") > adaptSteps = 1000 > burnInSteps = 3000 > nChains = 3 > numSavedSteps = 3000 > thinSteps = 10 > nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains) > > library(R2jags) > rnorm(1)
[1] 1.184
> jags.m.T.time <- system.time( + data.r2jags.m.T <- jags(data=data.list, + inits=NULL, + parameters.to.save=params, + model.file="../downloads/BUGSscripts/tut9.9jagsM.T.txt", + n.chains=3, + n.iter=nIter, + n.burnin=burnInSteps, + n.thin=thinSteps + ) + )
Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 3621 Initializing model
> print(data.r2jags.m.T)
Inference for Bugs model at "../downloads/BUGSscripts/tut9.9jagsM.T.txt", fit using jags,
3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
alpha[1] 214.02 12.032 188.96 206.04 214.22 222.22 237.854 1.001 3000
alpha[2] -42.10 16.845 -74.74 -53.87 -42.25 -31.36 -8.952 1.001 2500
alpha[3] -42.38 17.227 -75.71 -53.60 -42.82 -31.03 -7.684 1.001 3000
alpha[4] 27.63 1.523 24.68 26.60 27.64 28.63 30.718 1.001 3000
alpha[5] -17.35 2.146 -21.55 -18.78 -17.32 -15.88 -13.248 1.002 1300
alpha[6] -28.21 2.223 -32.62 -29.63 -28.20 -26.72 -23.849 1.001 3000
sigma 48.48 1.930 45.02 47.14 48.38 49.76 52.374 1.001 3000
sigma.B 23.49 4.377 15.89 20.38 23.26 26.26 32.708 1.001 3000
deviance 3708.62 9.521 3692.03 3701.92 3707.91 3714.59 3728.740 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 45.3 and DIC = 3754.0
DIC is an estimate of expected predictive error (lower deviance is better).
> data.mcmc.list.m.T <- as.mcmc(data.r2jags.m.T) > Data.mcmc.list.m.T <- data.mcmc.list.m.T
JAGS Matrix [1,] "13000" [2,] "10" [3,] "3000" [4,] "0.0419" [5,] "214.22 [190.26 , 238.39]" [6,] "-42.25 [-74.22 , -8.81]" [7,] "-42.82 [-75.74 , -7.79]" [8,] "27.64 [24.53 , 30.47]" [9,] "-17.32 [-21.60 , -13.27]" [10,] "-28.20 [-32.79 , -24.13]" [11,] "48.37 [45.00 , 52.36]" [12,] "23.26 [15.56 , 32.13]" [13,] "11.45" [14,] "0.02" [15,] "11.51" [16,] "0.00" [17,] "0.00"
