Jump to main navigation

«
»

Tutorial 6.2a - t-tests

21 May 2017

Two independent sample t-tests

As a starting point for this two sample t-tests, we will generate some fabricated representing a single response collected from two populations (Population A and Population B). The characteristics of the populations (which are obviously not normally known - rather these are the parameters that we seek to estimate and make inferences about) as well as some aspects of the experimental design used to collect the observations are:

  • the mean of Population 1 is 105
  • the mean of Population 2 is 77.5
  • both populations have a standard deviation of 3.0
  • Population 1 and 2 were sampled with $n=60$ and $n=40$ respectively

Details of data generation
set.seed(1)
nA <- 60  #sample size from Population A
nB <- 40  #sample size from Population B
muA <- 105  #population mean of Population A
muB <- 77.5  #population mean of Population B
sigma <- 3.0  #standard deviation of both populations (equally varied)
yA <- rnorm(nA, muA, sigma)  #Population A sample
yB <- rnorm(nB, muB, sigma)  #Population B sample
y <- c(yA, yB)
x <- factor(rep(c("A", "B"), c(nA, nB)))  #categorical listing of the populations
data <- data.frame(y, x)  # dataset

Assumptions and exploratory data analysis

We are going to use the samples to estimate the population means as well as test the null hypothesis that the populations are equal (i.e. that the population means are the same - Population A minus Population b equals 0).

This simple null hypothesis can be tested using a t-test. However, for the test to be reliable, it assumes that:

  • the populations from which the samples were collected were normally distributed
  • the populations from which the samples were collected were equally varied
  • the collected samples represented the populations in an unbiased manner

The last of these assumptions can only be addressed at the design and data collection phase. These fabricated data were generated from equally varied normal distributions and thus should adhere to the other two assumptions. Nevertheless, boxplots are a useful diagnotic. 

boxplot(y~x, data)
plot of chunk tut6.2aS1.1
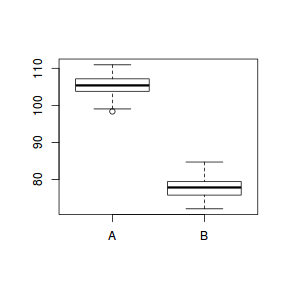
tapply(data$y, data$x,var)

       A        B 
6.581824 8.474237
There is no evidence of non-normality nor gross heteroscedasticity (non-homogeneity of variance). The samples variances are not wildly different (yet are not the same).

In R, pooled-variances (student) and separate variances (Welch test) t-test are performed using the t.test() function.

  • For pooled-variances t-test: 
    t.test(y~x, data, var.equal=TRUE)

    	Two Sample t-test

data:  y by x
t = 49.727, df = 98, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 26.39339 28.58754
sample estimates:
mean in group A mean in group B 
      105.32285        77.83238
  • For separate-variances t-test: 
    t.test(y~x, data, var.equal=FALSE)

    	Welch Two Sample t-test

data:  y by x
t = 48.479, df = 76.318, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 26.36115 28.61978
sample estimates:
mean in group A mean in group B 
      105.32285        77.83238
Whether using a pooled or separate variances t-test, the conclusions are the same: reject the null hypothesis that the populations are the same. The response of Population A is significantly higher than that of Population B.

The 95% confidence intervals indicate 95% of such intervals (intervals spanning a sample difference of 26.36-28.59 units) would contain the true mean.

Paired samples t-test

Lets generate some more fabricated data of a single response collected from pairs of samples representing sites sampled before and after an impact. In this case, there is actually only a single population (the difference between before and after). The degree to which sites respond to the impact differs from site to site (the variability) The characteristics of the populations and samples are:

  • the mean before response value is 100
  • the mean effect on this response after the impact is +30
  • the variability of the effect is 5.0
  • the variability of the sites is 20
  • There were $n=25$ sites before and after the impact

Details of data generation
set.seed(1)
n.sites <- 25
n.repeats <- 2
n <- n.sites * n.repeats
before <- 100
site.sd <- 20
ba.effect <- 30
sigma <- 15

int.effects <- rnorm(n=n.sites, mean=before, sd=site.sd)
ba <- gl(2,1,n, lab=c("Before","After"))
ba.effects <- rep(ba.effect,n.sites)
sites <- gl(n = n.sites, k = n.repeats)

all.effects <- c(int.effects, ba.effects)
Xmat <- model.matrix(~-1+sites*ba-ba)
lin.pred <- Xmat[,] %*% all.effects
eps <- rnorm(n=n,mean=0, sd=sigma)
y <- lin.pred + eps
data1 <- data.frame(y,sites,ba)
#check some of the properties
#before and after means
with(data1, tapply(y,ba,mean))

  Before    After 
104.2735 135.4377 

#site standard deviation
sqrt(var(with(data1, tapply(y,sites,mean))))

[1] 21.32765

#traditional wide format
library(reshape)
data2 <- cast(data1,sites~ba, value="y")

Assumptions and exploratory data analysis

A paired t-test is essentially a one sample t-test of the differences between each pair (the null hypothesis is that the mean difference equals zero). Therefore, the regular assumptions pertain to the differences

Using the repeated measures (wide) data format, we create a new column that is the difference between the before and after columns - this mimics the response. 

data2<-within(data2, Diff <- After-Before)

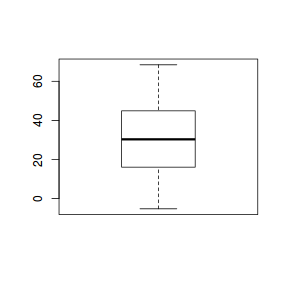
As with a regular t-test, normality can be explored using boxplots. 

boxplot(data2$Diff)
plot of chunk tut6.2aS2.2
There is no evidence of non-normality.

In R, paired t-test are also performed using the t.test() function. 

t.test(data2$After, data2$Before, paired=TRUE)

	Paired t-test

data:  data2$After and data2$Before
t = 7.6622, df = 24, p-value = 6.714e-08
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 22.76984 39.55870
sample estimates:
mean of the differences 
               31.16427
We would reject the null hypothesis that the difference between before and after is equal to zero. The impact results in a significant increase in the response. On average the impact lead to an increase in response of 31.16 units.


Worked examples

Basic statistics references
  • Logan (2010) - Chpt 6
  • Quinn & Keough (2002) - Chpt 6

Hypothesis testing

Furness & Bryant (1996) studied the energy budgets of breeding northern fulmars (Fulmarus glacialis) in Shetland. As part of their study, they recorded the body mass and metabolic rate of eight male and six female fulmars.

Download Furness data set
Format of furness.csv data files
SEXMETRATEBODYMASS
MALE2950875
FEMALE1956765
MALE2308780
MALE2135790
MALE1945788

SEXSex of breeding northern fulmars (Fulmarus glacialis)
METRATEMetabolic rate (hJ/day)
BODYMASSBody mass (g)
Northern fulmars

Open the furness data file.

Show code
furness <- read.csv('../downloads/data/furness.csv',header=T, strip.white=TRUE)
head(furness)

     SEX METRATE BODYMASS
1   Male  2950.0      875
2 Female  1956.1      635
3   Male  2308.7      765
4   Male  2135.6      780
5   Male  1945.6      790
6 Female  1490.5      635
  1. The researchers were interested in testing whether there is a difference in the metabolic rate of male and female breeding northern fulmars. In light of this, list the following:
    1. The biological hypotheses of interest
    2. The biological null hypotheses
    3. The statistical null hypotheses (H0)

    2. The appropriate statistical test for testing the null hypothesis that the means of two independent populations are equal is a t-test

    Before proceeding, make sure you understand what is meant by normality and equal variance as well as the principles of hypothesis testing using a t-test.

  2. For the null hypothesis test of interest (that the mean population metabolic rate of males and females were the same), calculate the Degrees of freedom
    Show code
    #number of replicates in each group minus 2 (one for each population)
sum(with(furness, tapply(METRATE, SEX, length)))-2

    [1] 12
  3. Calculate the critical t-values for the following null hypotheses (&alpha = 0.05)
    1. The metabolic rate of males is higher than that females (one-tailed test) HINT
    2. The metabolic rate of males is the same as that of females (two-tailed test) HINT
    Show code
    qt(0.05,df=12,lower.tail=F)

    [1] 1.782288

    qt(0.05/2,df=12,lower.tail=F)

    [1] 2.178813

    4. Since most hypothesis tests follow the same basic procedure, confirm that you understand the basic steps of hypothesis tests

  4. In the table below, list the assumptions of a t-test along with how violations of each assumption are diagnosed and/or the risks of violations are minimized.
    AssumptionDiagnostic/Risk Minimization
    I.
    II.
    III.

    So, we wish to investigate whether or not male and female fulmars have the same metabolic rates, and that we intend to use a t-test to test the null hypothesis that the population mean metabolic rate of males is equal to the population mean metabolic rate of females. Having identified the important assumptions of a t-test, use the samples to evaluate whether the assumptions are likely to be violated and thus whether a t-test is likely to be reliability.

  5. Is there any evidence that; HINT
    1. The assumption of normality has been violated?
    2. The assumption of homogeneity of variance has been violated?
    Show code
    boxplot(METRATE~SEX, data=furness)
    plot of chunk Q1-5
  6. Perform a t-test to examine the effect of sex on the mass of fulmars using either (which ever is most appropriate) a pooled variance t-test (for when population variances are very similar HINT) or separate variance t-test (for when the variance of one population is likely to be up to 2.5 times greater or less than the other population HINT). Ensure that you are familiar with the output of a t-test.

    1. What is the t-value? (Excluding the sign. The sign will depend on whether you compared males to females or females to males, and thus only indicates which group had the higher mean).
    2. What is the df (degrees of freedom).
    3. What is the p value.
    Show code
    #Separate variance t-test is probably more reliable, as there is some evidence that the two populations are not exactly equal in variability
t.test(METRATE~SEX, equal.var=F,data=furness)

    	Welch Two Sample t-test

data:  METRATE by SEX
t = -0.77317, df = 10.468, p-value = 0.4565
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1075.3208   518.8042
sample estimates:
mean in group Female   mean in group Male 
            1285.517             1563.775
  7. Write the results out as though you were writing a research paper/thesis. For example (select the phrase that applies and fill in gaps with your results): 
    The mean metabolic rate of male fulmars was (choose correct option)
    (t = , df = , P = ) the mean metabolic rate of female fulmars.
  8. Construct a bar graph showing the mean metabolic rate of male and female fulmars and an indication of the precision of the means with error bars.
    Show code
    # calculate the means
means <- tapply(furness$METRATE, furness$SEX, mean)
# calculate the standard deviation
sds <- tapply(furness$METRATE, furness$SEX, sd)
# calculate the lengths
ns <- tapply(furness$METRATE, furness$SEX, length)
# calculate the standard errors
ses <- sds/sqrt(ns)
# plot the bars
xs <- barplot(means,beside=T)
# load package containing error bar function
library(Hmisc)
# plot the error bars
errbar(xs, means, means+ses, means-ses, add=T)
    plot of chunk Q1-8
    Show code
    # set the size of the figure margins
opar<-par(mar=c(4,5,0,0))
# calculate the means
means <- tapply(furness$METRATE, furness$SEX, mean)
# calculate the standard deviation
sds <- tapply(furness$METRATE, furness$SEX, sd)
# calculate the lengths
ns <- tapply(furness$METRATE, furness$SEX, length)
# calculate the standard errors
ses <- sds/sqrt(ns)
#calculate the data limits
lim <- max(means+ses)
# plot the bars
xs <- barplot(means,beside=T, axes=FALSE, ann=FALSE, ylim=c(0,lim))
# plot the error bars
arrows(xs,means-ses,xs,means+ses, len=0.1, ang=90, code=3)
# generate the axes
mtext("Sex",1, line=2.5, cex=2)
axis(2,las=1)
mtext("Metabolic rate",2,line=3.5, cex=2)
box(bty="l")
    plot of chunk Q1-9
    Show ggplot code
    library(ggplot2)
library(plyr)
library(gmodels)
dat <- ddply(furness, ~SEX, function(x) {
  data.frame(Metrate=mean(x$METRATE), t(ci(x$METRATE)))
})
head(dat)

         SEX  Metrate Estimate CI.lower CI.upper Std..Error
1 Female 1285.517 1285.517 843.7436 1727.290   171.8572
2   Male 1563.775 1563.775 816.0607 2311.489   316.2085

    ggplot(dat, aes(y=Metrate, x=SEX)) +
  geom_point(data=furness, aes(y=METRATE, x=SEX), color='grey')+
  geom_pointrange(aes(ymin=CI.lower, ymax=CI.upper))+
  scale_y_continuous(expression(Metabolic~rate~(HJ/day)))+
  scale_x_discrete('')+
  theme_classic()+theme(axis.title.y=element_text(vjust=2, size=rel(1.25), face='bold'))
    plot of chunk Q1-10

Paired data

Here is a modified example from Quinn and Keough (2002). Elgar et al. (1996) studied the effect of lighting on the web structure or an orb-spinning spider. They set up wooden frames with two different light regimes (controlled by black or white mosquito netting), light and dim. A total of 17 orb spiders were allowed to spin their webs in both a light frame and a dim frame, with six days `rest' between trials for each spider, and the vertical and horizontal diameter of each web was measured. Whether each spider was allocated to a light or dim frame first was randomized. The H0's were that each of the two variables (vertical diameter and horizontal diameter of the orb web) were the same in dim and light conditions. Elgar et al. (1996) correctly treated these as paired comparisons because the same spider spun her web in a light frame and a dark frame.

Download Elgar data set
Format of elgar.csv data files
PAIRVERTDIMHORIZDIMVERTLIGHHORIZLIGH
..........
..........
..........

PAIRName given to each pair of webs spun by a particular spider
VERTDIMThe vertical dimension or height (mm) of webs spun in dim conditions
HORIZDIMThe horizontal dimension or width (mm) of webs spun in dim conditions
VERTLIGHThe vertical dimension or height (mm) of webs spun in light conditions
HORIZLIGHThe horizontal dimension or width (mm) of webs spun in light conditions
Coastal orb-weaving spider
Note:for paired t-tests, it is traditional for categories to be column labels rather than entries in a categorical variable. Compare the structure of the elgar data (paired t-test) set with that of the furness (standard t-test) data set.

Open the elgar data file.

Show code
elgar <- read.csv("../downloads/data/elgar.csv", header=T, strip.white=T)
head(elgar)

  PAIR VERTDIM HORIZDIM VERTLIGHT HORIZLIGHT
1    K     300      295        80         60
2    M     240      260       120        140
3    N     250      280       170        160
4    O     220      250        90        120
5    P     160      160       150        180
6    R     170      150       110         90
  1. What is an appropriate statistical test for testing an hypothesis about the difference in dimensions of webs spun in light versus dark conditions? Explain why?
  2. The actual H0 is that the mean of the differences between the pairs (light and dim for each spider) equals zero. Use a paired t-test to test the H0 that the mean of the differences in vertical diameter (HINT) and separately, in horizontal diameter (HINT) of the web between the pairs (light and dim for each spider) equal zero.
    Show code
    t.test(elgar$VERTDIM,elgar$VERTLIGHT, paired=T)

    	Paired t-test

data:  elgar$VERTDIM and elgar$VERTLIGHT
t = 0.96545, df = 16, p-value = 0.3487
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -24.61885  65.79532
sample estimates:
mean of the differences 
               20.58824 

    t.test(elgar$HORIZDIM,elgar$HORIZLIGHT, paired=T)

    	Paired t-test

data:  elgar$HORIZDIM and elgar$HORIZLIGHT
t = 2.1482, df = 16, p-value = 0.04735
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.6085725 91.7443687
sample estimates:
mean of the differences 
               46.17647
  3. Write the results out as though you were writing a research paper/thesis. For example (select the phrase that applies and fill in gaps with your results): 
    The mean vertical diameter of spider webs in dim conditions was (choose correct option)
    (t = , df = , P = )
    the vertical dimensions in light conditions.
    The mean horizontal diameter of spider webs in dim conditions was (choose correct option)
    (t = , df = , P = )
    the horizontal dimensions in light conditions.

Non-parametric tests

We will now revisit the data set of Furness & Bryant (1996) that was used in Question 4 to investigate the effects of gender on the metabolic rates of breeding northern fulmars (Fulmarus glacialis). Furness & Bryant (1996) also recorded the body mass of the eight male and six female fulmars they captured.

Since the males and female fulmars were all independent of one another, a t-test would be appropriate to test the null hypothesis of no difference in mean body weight of male and female fulmars.

  1. Are the assumptions underlying this test met? (Y or N) Hint: check the relative sizes of the two sample variances and the distribution of body weight for each sex.
    Show code
    boxplot(BODYMASS~SEX, data=furness)
    plot of chunk Q3-1
    tapply(furness$BODYMASS,furness$SEX,mean)

    Female   Male 
643.00 839.75 

    tapply(furness$BODYMASS,furness$SEX,var)

      Female     Male 
 166.000 6214.786

    2. When the distributional assumptions are violated, parametric tests are unreliable. Under these circumstances, non-parametric tests can be very useful.

  2. The Wilcoxon-Mann-Whitney test is described as a non-parametric test for comparing two groups.
    1. What null hypothesis does this test actually evaluate?
    2. What are the underlying assumptions of a Wilcoxon-Mann-Whitney test?
  3. If the assumptions are met, test the null hypothesis of no difference in body weight between male and female fulmars using a Wilcoxon test HINT. Based on this outcome, what are your conclusions?
    1. Statistical:
    2. Biological (include trend):
    Show code
    wilcox.test(BODYMASS~SEX, data=furness)

    	Wilcoxon rank sum test with continuity correction

data:  BODYMASS by SEX
W = 0, p-value = 0.002309
alternative hypothesis: true location shift is not equal to 0
  4. Construct a bar graph showing the mean mass of male and female fulmars and an indication of the precision of the means with error bars.
    Show code
    ##use ggplot to calculate bootstrap confidence intervals and means
ggplot(furness, aes(y=METRATE, x=SEX)) +
  geom_point(data=furness, aes(y=METRATE, x=SEX), color='grey')+
  geom_pointrange(stat='summary', fun.data='mean_cl_boot')+
  scale_y_continuous(expression(Metabolic~rate~(HJ/day)))+
  scale_x_discrete('')+
  theme_classic()+theme(axis.title.y=element_text(vjust=2, size=rel(1.25), face='bold'))
    plot of chunk Q3-4
Centering variables

Centering a variable shifts the underlying scale such that the mean of the variable is equal to 0. That is, once centered, the data will vary around 0.

Centering is achieved by subtracting each value from the mean of all the values. In R this can be done manually: 

Y <- c(1,4,3,7,8)
mean(Y)

[1] 4.6

Yc <- Y-mean(Y)
Or using the scale() function. 
scale(Y, scale=FALSE)

     [,1]
[1,] -3.6
[2,] -0.6
[3,] -1.6
[4,]  2.4
[5,]  3.4
attr(,"scaled:center")
[1] 4.6
The scale() function can also be used to center the vectors of matrices. 
Y <- matrix(c(2,5,3,6,7,1,7,3,5),3,3)
scale(Y,scale=FALSE)

           [,1]      [,2] [,3]
[1,] -1.3333333  1.333333    2
[2,]  1.6666667  2.333333   -2
[3,] -0.3333333 -3.666667    0
attr(,"scaled:center")
[1] 3.333333 4.666667 5.000000

End of instructions

  Normal probabilities

> pnorm(c(value), mean=mean, sd=sd, lower.tail=FALSE)

this will calculate the area under a normal distribution (beyond the value of value) with mean of mean and standard deviation of sd. The argument lower.tail=FALSE indicates that the area is calculated for values greater than value. For example

> pnorm(c(2.9), mean=2.025882, sd=0.4836265, lower.tail=FALSE)

End of instructions

  Boxplots

A boxplot is a graphical representation of the distribution of observations based on the 5-number summary that includes the median (50%), quartiles (25% and 75%) and data range (0% - smallest observation and 100% - largest observation). The box demonstrates where the middle 50% of the data fall and the whiskers represent the minimum and maximum observations. Outliers (extreme observations) are also represented when present.
The figure below demonstrates the relationship between the distribution of observations and a boxplot of the same observations. Normally distributed data results in symmetrical boxplots, whereas skewed distributions result in asymmetrical boxplots with each segment getting progressively larger (or smaller).

End of instructions

  Boxplots

> boxplot(variable)

where variable is the name of the numeric vector (variable)

End of instructions

  Observations, variables & populations

Observations are the sampling units (e.g quadrats) or experimental units (e.g. individual organisms, aquaria) that make up the sample.

Variables are the actual properties measured by the individual observations (e.g. length, number of individuals, rate, pH, etc). Random variables (those variables whose values are not known for sure before the onset of sampling) can be either continuous (can theoretically be any value within a range, e.g. length, weight, pH, etc) or categorical (can only take on certain discrete values, such as counts - number of organisms etc).

Populations are defined as all the possible observations that we are interested in.

A sample represents a collected subset of the population's observations and is used to represent the entire population. Sample statistics are the characteristics of the sample (e.g. sample mean) and are used to estimate population parameters.

End of instructions

  Population & sample

A population refers to all possible observations. Therefore, population parameters refer to the characteristics of the whole population. For example the population mean.

A sample represents a collected subset of the population's observations and is used to represent the entire population. Sample statistics are the characteristics of the sample (e.g. sample mean) and are used to estimate population parameters.

End of instructions

  Standard error and precision

A good indication of how good a single estimate is likely to be is how precise the measure is. Precision is a measure of how repeatable an outcome is. If we could repeat the sampling regime multiple times and each time calculate the sample mean, then we could examine how similar each of the sample means are. So a measure of precision is the degree of variability between the individual sample means from repeated sampling events.

Sample number Sample mean
112.1
212.7
312.5
Mean of sample means12.433
> SD of sample means0.306

The table above lists three sample means and also illustrates a number of important points;
  1. Each sample yields a different sample mean
  2. The mean of the sample means should be the best estimate of the true population mean
  3. The more similar (consistent) the sample means are, the more precise any single estimate of the population mean is likely to be
The standard deviation of the sample means from repeated sampling is called the Standard error of the mean.

It is impractical to repeat the sampling effort multiple times, however, it is possible to estimate the standard error (and therefore the precision of any individual sample mean) using the standard deviation (SD) of a single sample and the size (n) of this single sample.

The smaller the standard error (SE) of the mean, the more precise (and possibly more reliable) the estimate of the mean is likely to be.

End of instructions

  Confidence intervals


A 95% confidence interval is an interval that we are 95% confident will contain the true population mean. It is the interval that there is a less than 5% chance that this interval will not contain the true population mean, and therefore it is very unlikely that this interval will not contain the true mean. The frequentist approach to statistics dictates that if multiple samples are collected from a population and the interval is calculated for each sample, 95% of these intervals will contain the true population mean and 5% will not. Therefore there is a 95% probability that any single sample interval will contain the population mean.

The interval is expressed as the mean ± half the interval. The confidence interval is obviously affected by the degree of confidence. In order to have a higher degree of confidence that an interval is likely to contain the population mean, the interval would need to be larger.

End of instructions

  Successful transformations


Since the objective of a transformation is primarily to normalize the data (although variance homogeneity and linearization may also be beneficial side-effects) the success of a transformation is measured by whether or not it has improved the normality of the data. It is not measured by whether the outcome of a statistical analysis is more favorable!

End of instructions

  Selecting subsets of data

# select the first 5 entries in the variable
> variable[1:5]
# select all but the first entry in the variable
> variable[-1]
# select all cases of variable that are less than num
> variable[variablenum]
# select all cases of variable that are equal to 'Big'
> variable1[variablelabel]

where variable is the name of a numeric vector (variable) and num is a number. variable1 is the name of a character vector and label is a character string (word). 5. In the Subset expression box enter a logical statement that indicates how the data is to be subsetted. For example, exclude all values of DOC that are greater than 170 (to exclude the outlier) and therefore only include those values that are less that 170, enter DOC < 170. Alternatively, you could chose to exclude the outlier using its STREAM name. To exclude this point enter STREAM. != 'Santa Cruz'.

End of instructions

  Summary Statistics by groups

> tapply(dv,factor,func)

the tapply() function applies the function func to the numeric vector dv for each level of the factor factor. For example

# calculate the mean separately for each group
> tapply(dv,factor,mean)
# calculate the mean separately for each group
> tapply(dv,factor,var)

End of instructions

  EDA - Normal distribution

Parametric statistical hypothesis tests assume that the population measurements follow a specific distribution. Most commonly, statistical hypothesis tests assume that the population measurements are normally distributed (Question 4 highlights the specific reasoning for this).

While it is usually not possible to directly examine the distribution of measurements in the whole population to determine whether or not this requirement is satisfied or not (for the same reasons that it is not possible to directly measure population parameters such as population mean), if the sampling is adequate (unbiased and sufficiently replicated), the distribution of measurements in a sample should reflect the population distribution. That is a sample of measurements taken from a normally distributed population should be normally distributed.

Tests on data that do not meet the distributional requirements may not be reliable, and thus, it is essential that the distribution of data be examined routinely prior to any formal statistical analysis.

End of instructions

  Factorial boxplots

> boxplot(dv~factor,data=data)

where dv is the name of the numeric vector (dependent variable), factor is the name of the factor (categorical or factor variable) and data is the name of the data frame (data set). The '~' is used in formulas to represent that the left hand side is proportional to the right hand side.

End of instructions

  EDA - Linearity

The most common methods for analysing the relationship or association between variables.assume that the variables are linearly related (or more correctly, that they do not covary according to some function other than linear). For example, to examine for the presence and strength of the relationship between two variables (such as those depicted below), it is a requirement of the more basic statistical tests that the variables not be related by any function other than a linear (straight line) function if any function at all.

There is no evidence that the data represented in Figure (a) are related (covary) according to any function other than linear. Likewise, there is no evidence that the data represented in Figure (b) are related (covary) according to any function other than linear (if at all). However, there is strong evidence that the data represented in Figure (c) are not related linearly. Hence Figure (c) depicts evidence for a violation in the statistical necessity of linearity.

End of instructions

  EDA - Scatterplots

Scatterplots are constructed to present the relationships, associations and trends between continuous variables. By convention, dependent variables are arranged on the Y-axis and independent variables on the X-axis. The variable measurements are used as coordinates and each replicate is represented by a single point.

Figure (c) above displays a linear smoother (linear `line-of-best-fit') through the data. Different smoothers help identify different trends in data.

End of instructions

  Scatterplots

# load the 'car' library
> library(car)
# generate a scatterplot
> scatterplot(dv~iv,data=data)

where dv is the dependent variable, iv is the independent variable and data is the data frame (data set).

End of instructions

  Plotting y against x


The statement 'plot variable1 against variable2' is interpreted as 'plot y against x'. That is variable1 is considered to be the dependent variable and is plotted on the y-axis and variable2 is the independent variable and thus is plotted on the x-axis.

End of instructions

  Scatterplot matrix (SPLOM)

# make sure the car package is loaded > library(car)
> scatterplot.matrix(~var1 + var2 + var3, data=data, diagonal='boxplot')
#OR > pairs(~var1 + var2 + var3, data=data)

where var1, var2 etc are the names of numeric vectors in the data data frame (data set)

End of instructions

  EDA - Homogeneity of variance

Many statistical hypothesis tests assume that the populations from which the sample measurements were collected are equally varied with respect to all possible measurements. For example, are the growth rates of one population of plants (the population treated with a fertilizer) more or less varied than the growth rates of another population (the control population that is purely treated with water). If they are, then the results of many statistical hypothesis tests that compare means may be unreliable. If the populations are equally varied, then the tests are more likely to be reliable.
Obviously, it is not possible to determine the variability of entire populations. However, if sampling is unbiased and sufficiently replicated, then the variability of samples should be directly proportional to the variability of their respective populations. Consequently, samples that have substantially different degrees of variability provide strong evidence that the populations are likely to be unequally varied.
There are a number of options available to determine the likelihood that populations are equally varied from samples.
1. Calculate the variance or standard deviation of the populations. If one sample is more than 2 times greater or less than the other sample(s), then there is some evidence for unequal population variability (non-homogeneity of variance)
2. Construct boxplots of the measurements for each population, and compare the lengths of the boxplots. The length of a symmetrical (and thus normally distributed) boxplot is a robust measure of the spread of values, and thus an indication of the spread of population values. Therefore if any of the boxplots are more than 2 times longer or shorter than the other boxplot(s), then there is again, some evidence for unequal population variability (non-homogeneity of variance)


End of instructions

  t test

The frequentist approach to hypothesis testing is based on estimating the probability of collecting the observed sample(s) when the null hypothesis is true. That is, how rare would it be to collect samples that displayed the observed degree of difference if the samples had been collected from identical populations. The degree of difference between two collected samples is objectively represented by a t statistic.

Where y1 and y2 are the sample means of group 1 and 2 respectively and √s²/n1 + s²/n2 represents the degree of precision in the difference between means by taking into account the degree of variability of each sample.
If the null hypothesis is true (that is the mean of population 1 and population 2 are equal), the degree of difference (t value) between an unbiased sample collected from population 1 and an unbiased sample collected from population 2 should be close to zero (0). It is unlikely that an unbiased sample collected from population 1 will have a mean substantially higher or lower than an unbiased sample from population 2. That is, it is unlikely that such samples could result in a very large (positive or negative) t value if the null hypothesis (of no difference between populations) was true. The question is, how large (either positive or negative) does the t value need to be, before we conclude that the null hypothesis is unlikely to be true?.

What is needed is a method by which we can determine the likelihood of any conceivable t value when null hypothesis is true. This can be done via simulation. We can simulate the collection of random samples from two identical populations and calculate the proportion of all possible t values.

Lets say a vivoculturalist was interested in comparing the size of Eucalyptus regnans seedlings grown under shade and full sun conditions. In this case we have two populations. One population represents all the possible E. regnans seedlings grown in shade conditions, and the other population represents all the possible E. regnans seedlings grown in full sun conditions. If we had grown 200 seedlings under shade conditions and 200 seedlings under full sun conditions, then these samples can be used to assess the null hypothesis that the mean size of an infinite number (population) of E. regnans seedlings grown under shade conditions is the same as the mean size of an infinite number (population) of E. regnans seedlings grown under full sun conditions. That is that the population means are equal.

We can firstly simulate the sizes of 200 seedlings grown under shade conditions and another 200 seedlings grown under full sun conditions that could arise naturally when shading has no effect on seedling growth. That is, we can simulate one possible outcome when the null hypothesis is true and shading has no effect on seedling growth
Now we can calculate the degree of difference between the mean sizes of seedlings grown under the two different conditions taking into account natural variation (that is, we can calculate a t value using the formula from above). From this simulation we may have found that the mean size of seedling grown in shade and full sun was 31.5cm and 33.7cm respectively and the degree of difference (t value) was 0.25. This represents only one possible outcome (t value). We now repeat this simulation process a large number of times (1000) and generate a histogram (or more correctly, a distribution) of the t value outcomes that are possible when the null hypothesis is true.

It should be obvious that when the null hypothesis is true (and the two populations are the same), the majority of t values calculated from samples containing 200 seedlings will be close to zero (0) - indicating only small degrees of difference between the samples. However, it is also important to notice that it is possible (albeit less likely) to have samples that are quit different from one another (large positive or negative t values) just by pure chance (for example t values greater than 2).

It turns out that it is not necessary to perform these simulations each time you test a null hypothesis. There is a mathematical formulae to estimate the t distribution appropriate for any given sample size (or more correctly, degrees of freedom) when the null hypothesis is true. In this case, the t distribution is for (200-1)+(200-1)=398 degrees of freedom.

At this stage we would calculate the t value from our actual observed samples (the 200 real seedlings grown under each of the conditions). We then compare this t value to our distribution of all possible t values (t distribution) to determine how likely our t value is when the null hypothesis is true. The simulated t distribution suggests that very large (positive or negative) t values are unlikely. The t distribution allows us to calculate the probability of obtaining a value greater than a specific t value. For example, we could calculate the probability of obtaining a t value of 2 or greater when the null hypothesis is true, by determining the area under the t distribution beyond a value of 2.

If the calculated t value was 2, then the probability of obtaining this t value (or one greater) when the null hypothesis is true is 0.012 (or 1.2%). Since the probability of obtaining our t value or one greater (and therefore the probability of having a sample of 200 seedlings grown in the shade being so much different in size than a sample of 200 seedlings grown in full sun) is so low, we would conclude that the null hypothesis of no effect of shading on seedling growth is likely to be false. Thus, we have provided some strong evidence that shading conditions do effect seedling growth!


End of instructions

  t-test degrees of freedom

Degrees of freedom is the number of observations that are free to vary when estimating a parameter. For a t-test, df is calculated as
df = (n1-1)+(n2-1)
where n1 is population 1 sample size and n2 is the sample size of population 2.

End of instructions

  One-tailed critical t-value

One-tail critical t-values are just calculated from a t distribution (of given df). The area under the t distribution curve above (or below) this value is 0.05 (or some other specified probability). Essentially we calculate a quantile of a specified probability from a t distribution of df degrees of freedom

# calculate critical t value (&alpha =0.05) for upper tail (e.g. A larger than B)
> qt(0.05,df=df,lower.tail=F)
# calculate critical t value (&alpha =0.05) for lower tail (e.g. B larger than A)
> qt(0.05,df=df,lower.tail=T)

where 0.05 is the specified &alpha value and df is the specified degrees of freedom. Note that it is not necessary to have collected the data before calculating the critical t-value, you only need to know sample sizes (to get df).

It actually doesn't matter whether you select Lower tail is TRUE or FALSE. The t-distribution is a symmetrical distribution, centered around 0, therefore, the critical t-value is the same for both Lower tail (e.g. population 2 greater than population 1) and Upper tail (e.g. population 1 greater than population 2), except that the Lower tail is always negative. As it is often less confusing to work with positive values, it is recommended that you use Upper tail values. An example of a t-distribution with Upper tail for a one-tailed test is depicted below. Note that this is not part of the t quantiles output!


End of instructions

  Two-tailed critical t-value

Two-tail critical t-values are just calculated from a t distribution (of given df). The area under the t distribution curve above and below the positive and negative of this value respectively is 0.05 (or some other specified probability). Essentially we calculate a quantile of a specified probability from a t distribution of df degrees of freedom. In a two-tailed test, half of the probability is associated with the area above the positive critical t-value and the other half is associated with the area below the negative critical t-value. Therefore when we use the quantile to calculate this critical t-value, we specify the probability as &alpha/2 - since &alpha/2 applies to each tail.

# calculate critical t value (&alpha =0.05) for upper tail (e.g. A different to B)
> qt(0.05/2,df=df, lower.tail=T)

where 0.05 is the specified &alpha value and df is the specified degrees of freedom. Note that it is not necessary to have collected the data before calculating the critical t-value, you only need to know sample sizes (to get df).

Again, it actually doesn't matter whether you select Lower tail as either TRUE or FALSE. For a symmetrical distribution, centered around 0, the critical t-value is the same for both Lower tail (e.g. population 2 greater than population 1) and Upper tail (e.g. population 1 greater than population 2), except that the Lower tail is always negative. As it is often less confusing to work with positive values, it is recommended that you use Upper tail values. An example of a t-distribution with Upper tail for a two-tailed test is depicted below. Note that this is not part of the t quantiles output!

End of instructions

  Basic steps of Hypothesis testing


Step 1 - Clearly establish the statistical null hypothesis. Therefore, start off by considering the situation where the null hypothesis is true - e.g. when the two population means are equal

Step 2 - Establish a critical statistical criteria (e.g. alpha = 0.05)

Step 3 - Collect samples consisting of independent, unbiased samples

Step 4 - Assess the assumptions relevant to the statistical hypothesis test. For a t test:
  1.  Normality
  2.  Homogeneity of variance

Step 5 - Calculate test statistic appropriate for null hypothesis (e.g. a t value)


Step 6 - Compare observed test statistic to a probability distribution for that test statistic when the null hypothesis is true for the appropriate degrees of freedom (e.g. compare the observed t value to a t distribution).

Step 7 - If the observed test statistic is greater (in magnitude) than the critical value for that test statistic (based on the predefined critical criteria), we conclude that it is unlikely that the observed samples could have come from populations that fulfill the null hypothesis and therefore the null hypothesis is rejected, otherwise we conclude that there is insufficient evidence to reject the null hypothesis. Alternatively, we calculate the probability of obtaining the observed test statistic (or one of greater magnitude) when the null hypothesis is true. If this probability is less than our predefined critical criteria (e.g. 0.05), we conclude that it is unlikely that the observed samples could have come from populations that fulfill the null hypothesis and therefore the null hypothesis is rejected, otherwise we conclude that there is insufficient evidence to reject the null hypothesis.

End of instructions

  Pooled variance t-test

> t.test(dv~factor,data=data,var.equal=T)

where dv is the name of the dependent variable, factor is the name of the categorical/factorial variable and data is the name of the data frame (data set). The argument var.equal=T indicates a pooled variances t-test

End of instructions

  Separate variance t-test

> t.test(dv~factor,data=data,var.equal=F)

where dv is the name of the dependent variable, factor is the name of the categorical/factorial variable and data is the name of the data frame (data set). The argument var.equal=F indicates a separate variances t-test

End of instructions

  Output of t-test


The following output are based on a simulated data sets;
1.  Pooled variance t-test for populations with equal (or nearly so) variances

2.  Separate variance t-test for population with unequal variances

End of instructions

  R bargraph
 


# set the size of the figure margins
opar<-par(mar=c(4,5,0,0))
# calculate the means
means <- tapply(furness$METRATE, furness$SEX, mean)
# calculate the standard deviation
sds <- tapply(furness$METRATE, furness$SEX, sd)
# calculate the lengths
ns <- tapply(furness$METRATE, furness$SEX, length)
# calculate the standard errors
ses <- sds/sqrt(ns)
#calculate the data limits
lim <- max(means+ses)
# plot the bars
xs <- barplot(means,beside=T, axes=FALSE, ann=FALSE, ylim=c(0,lim))
# plot the error bars
arrows(xs,means-ses,xs,means+ses, len=0.1, ang=90, code=3)
# generate the axes
mtext("Sex",1, line=2.5, cex=2)
axis(2,las=1)
mtext("Metabolic rate",2,line=3.5, cex=2)
box(bty="l")
plot of chunk Q1-9

End of instructions

  Paired t-test

> t.test(cat1, cat2, data=data, paired=T)

where cat1 and cat2 are two numeric vectors (variables) in the data data frame (data set). The argument paired=T indicates a paired t-test)

End of instructions

  Non-parametric tests

Non-parametric tests do not place any distributional limitations on data sets and are therefore useful when the assumption of normality is violated. There are a number of alternatives to parametric tests, the most common are;

1. Randomization tests - rather than assume that a test statistic calculated from the data follows a specific mathematical distribution (such as a normal distribution), these tests generate their own test statistic distribution by repeatedly re-sampling or re-shuffling the original data and recalculating the test statistic each time. A p value is subsequently calculated as the proportion of random test statistics that are greater than or equal to the test statistic based on the original (un-shuffled) data.

2. Rank-based tests - these tests operate not on the original data, but rather data that has first been ranked (each observation is assigned a ranking, such that the largest observation is given the value of 1, the next highest is 2 and so on). It turns out that the probability distribution of any rank based test statistic for a is identical.

End of instructions

  Wilcoxon test

> wilcox.test(dv ~ factor, data=data)

where dv is the dependent variable and factor is the categorical variable from the data data frame (data set).

End of instructions

  Randomization (permutation) tests

The basis of hypothesis testing (when comparing two populations) is to determine how often we would expect to collect a specific sample (or more one more unusual) if the populations were identical. That is, would our sample be considered unusual under normal circumstances? To determine this, we need to estimate what sort of samples we would expect under normal circumstances. The theoretical t-distribution mimics what it would be like to randomly resample repeatedly (with a given sample size) from such identical populations.

A single sample from the (proposed) population(s) provides a range of observations that are possible. Completely shuffling those data (or labels), should mimic the situation when there is no effect (null hypothesis true situation), since the data are then effectively assigned randomly with respect to the effect. In the case of a t-test comparing the means of two groups, randomly shuffling the data is likely to result similar group means. This provides one possible outcome (t-value) that might be expected when the null hypothesis true. If this shuffling process is repeated multiple times, a distribution of all of the outcomes (t-values) that are possible when the null hypothesis is true can be generated. We can now determine how unusual our real (unshuffled) t-value is by comparing it to the built up t-distribution. If the real t-value is expected to occur less than 5% of the time, we reject the null hypothesis.

Randomization tests - rather than assume that a test statistic calculated from the data follows a specific mathematical distribution (such as a normal distribution), these tests generate their own test statistic distribution by repeatedly re-sampling or re-shuffling the original data and recalculating the test statistic each time. A p value is subsequently calculated as the proportion of random test statistics that are greater than or equal to the test statistic based on the original (un-shuffled) data.

End of instructions

  Defining the randomization statistic
 

stat <- function(data, indices){
t <- t.test(data[,2]~data[,1])$stat
t
}
The above function takes a data set (data) and calculates a test statistic (in this case a t-statistic). The illustrated function uses the t.test() function to perform a t-test on column 2 ([,2]) against column 1 ([,1]). The value of the t-statistic is stored in an object called 't'. The function returns the value of this object. The indentations are not important, they are purely used to improve human readability.

End of instructions

  Defining the data shuffling procedure
 

rand.gen <- function(data, mle){
out <- data
out[,1] <- sample(out[,1], replace=F)
out
}
The above function defines how the data should be shuffled. The first line creates a temporary object (out) that stores the original data set (data) so that any alterations do not effect the original data set. The second line uses the sample() function to shuffle the first column (the group labels). The third line of the function just returns the shuffled data set.

End of instructions

  Perform randomization test (bootstrapping)
 

library(boot)
coots.boot <- boot(coots, stat, R=100, sim="parametric", ran.gen=rand.gen)

Error in NROW(data): object 'coots' not found
The sequence begins by ensuring that the boot package has been loaded into memory. Then the boot() function is used to repeatedly (R=100: repeat 100 times) perform the defined statistical procedure (stat). The ran.gen=rand.gen parameter defines how the data set should be altered prior to performing the statistical procedure, and the sim="parametric" parameter indicates that all randomizations are possible (as opposed to a permutation where each configuration can only occur once). The outcome of the randomization test (bootstrap) is stored in an object called coots.boot

End of instructions

  Calculating p-value from randomization test
 

p.length <- length(coots.boot$t[coots.boot$t >= coots.boot$t0])+1

Error in eval(expr, envir, enclos): object 'coots.boot' not found

print(p.length/(coots.boot$R + 1))

Error in print(p.length/(coots.boot$R + 1)): object 'p.length' not found
The coots.boot object contains a list of all of the t-values calculated from the resampling (shuffling and recalculating) procedure (coots.boot$t)as well as the actual t-value from the actual data set (coots.boot$t0). It also stores the number of randomizations that it performed (coots.boot$R).

The first line in the above sequence determines how many of the possible t values (including the actual t-value) are greater or equal to the actual t-value. It does this by specifying a list of coots.boot$t values that are greater or equal to the coots.boot$t0 value. (coots.boot$t[coots.boot$t >= coots.boot$t0]) and calculating the length of this list using the length() function. One (1) is added to this length, since the actual t-value must be included as a possible t-value.
The second line expresses the number of randomization t-values greater or equal to the actual t-value as a fraction of the total number of randomizations (again adding 1 to account for the actual situation). This is interpreted as any other p-value - the probability of obtaining our sample statistic (and thus our observations) when the null hypothesis is true.

End of instructions

  Calculating p-value from randomization test

In a t-test, the effect size is the absolute difference between the expected population means. Therefore if the expected population means of population A and B are 10 and 16 respectively, then the effect size is 6.

Typically, effect size is estimated by considering the magnitude of an effect that is either likely or else what magnitude of effect would be regarded biologically significant. For example, if the overall population mean was estimated to be 12 and the researches regarded a 15% increase to be biologically significant, then the effect size is the difference between 12 and a mean 15% greater than 12 (12+(12*.15)=13.8). Therefore the effect size is (13.8-12=1.8).

End of instructions