Tutorial 11.4a -Logistic regression
23 April 2011
Binary data
Scenario and Data
Logistic regression is a type of generalized linear model (GLM) that models a binary response against a linear predictor via a specific link function. The linear predictor is the typically a linear combination of effects parameters (e.g. $\beta_0 + \beta_1x_x$). The role of the link function is to transform the expected values of the response y (which is on the scale of (0,1), as is the binomial distribution from which expectations are drawn) into the scale of the linear predictor (which is $-\infty,\infty$). GLM's transform the expected values (via a link) whereas LM's transform the observed data. Thus while GLM's operate on the scale of the original data and yet also on a scale appropriate of the residuals, LM's do neither.
There are many ways (transformations) that can map values on the (0,1) scale into values on the ($-\infty,\infty$) scale, however, the three most common are:
- logit: $log\left(\frac{\pi}{1-\pi}\right)$ - log odds ratio
- probit: $\phi^{-1}(\pi)$ where $\phi^{-1}$ is an inverse normal cumulative density function
- complimentary log-log: $log(-log(1-\pi))$
Lets say we wanted to model the presence/absence of an item ($y$) against a continuous predictor ($x$) As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped. Consequently, I have folded (toggled) this section away.
- the sample size = 20
- the continuous $x$ variable is a random uniform spread of measurements between 1 and 20
- the rate of change in log odds ratio per unit change in x (slope) = 0.5. The magnitude of the slope is an indicator of how abruptly the log odds ratio changes. A very abrupt change would occur if there was very little variability in the trend. That is, a large slope would be indicative of a threshold effect. A lower slope indicates a gradual change in odds ratio and thus a less obvious and precise switch between the likelihood of 1 vs 0.
- the inflection point (point where the slope of the line is greatest) = 10. The inflection point indicates the value of the predictor ($x$) where the log Odds are 50% (switching between 1 being more likely and 0 being more likely). This is also known as the LD50.
- the intercept (which has no real interpretation) is equal to the negative of the slope multiplied by the inflection point
- to generate the values of $y$ expected at each $x$ value, we evaluate the linear predictor. These expected values are then transformed into a scale mapped by (0,1) by using the inverse logit function $\frac{e^{linear~predictor}}{1+e^{linear~predictor}}$
- finally, we generate $y$ values by using the expected $y$ values as probabilities when drawing random numbers from a binomial distribution. This step adds random noise to the expected $y$ values and returns only 1's and 0's.
> set.seed(8) > # The number of samples > n.x <- 20 > # Create x values that at uniformly distributed > # throughout the rate of 1 to 20 > x <- sort(runif(n = n.x, min = 1, max = 20)) > # The slope is the rate of change in log odds ratio > # for each unit change in x the smaller the slope, > # the slower the change (more variability in data > # too) > slope = 0.5 > # Inflection point is where the slope of the line > # is greatest this is also the LD50 point > inflect <- 10 > # Intercept (no interpretation) > intercept <- -1 * (slope * inflect) > # The linear predictor > linpred <- intercept + slope * x > # Predicted y values > y.pred <- exp(linpred)/(1 + exp(linpred)) > # Add some noise and make binomial > n.y <- rbinom(n = n.x, 20, p = 0.9) > y <- rbinom(n = n.x, size = 1, prob = y.pred) > dat <- data.frame(y, x)
With these sort of data, we are primarily interested in investigating whether there is a relationship between the binary response variable and the linear predictor (linear combination of one or more continuous or categorical predictors).
Exploratory data analysis and initial assumption checking
- All of the observations are independent - this must be addressed at the design and collection stages
- The response variable (and thus the residuals) should be matched by an appropriate distribution (in the case of a binary response - a binomial is appropriate).
- All observations are equally influential in determining the trends - or at least no observations are overly influential. This is most effectively diagnosed via residuals and other influence indices and is very difficult to diagnose prior to analysis
- the relationship between the linear predictor (right hand side of the regression formula) and the link function should be linear. A scatterplot with smoother can be useful for identifying possible non-linearity.
So lets explore linearity by creating a histogram of the predictor variable ($x$) and a scatterplot of the relationship between the response ($y$) and the predictor ($x$)
> hist(dat$x)
> # now for the scatterplot > plot(y ~ x, dat) > with(dat, lines(lowess(y ~ x)))
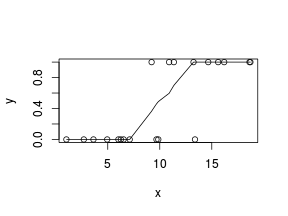
Conclusions: the predictor ($x$) does not display any skewness or other issues that might lead to non-linearity. The lowess smoother on the scatterplot does not display major deviations from a standard sigmoidal curve and thus linearity is satisfied. Violations of linearity could be addressed by either:
- define a non-linear linear predictor (such as a polynomial, spline or other non-linear function)
- transform the scale of the predictor variables
Model fitting or statistical analysis
We perform the logistic regression using the glm() function. The most important (=commonly used) parameters/arguments for logistic regression are:
- formula: the linear model relating the response variable to the linear predictor
- family: specification of the error distribution (and link function). Can be specified as either a string or as one of the family functions (which allows for the explicit declaration of the link function).
For examples:
- family="binomial" or equivalently family=binomial(link="logit")
- family=binomial(link="probit")
- data: the data frame containing the data
- weights: vector of weights to be used in the fitting process. These are particularly useful when dealing with grouped binary data from unequal sample sizes (see below).
I will demonstrate logistic regression with a range of possible link functions (each of which yield different parameter interpretations):
- logit
$$log\left(\frac{\pi}{1-\pi}\right)=\beta_0+\beta_1x_1+\epsilon_i, \hspace{1cm}\epsilon\sim Binom(\lambda)$$
> dat.glmL <- glm(y ~ x, data = dat, family = "binomial")
- probit
$$\phi^{-1}\left(\pi\right)=\beta_0+\beta_1x_1+\epsilon_i, \hspace{1cm}\epsilon\sim Binom(\lambda)$$
> dat.glmP <- glm(y ~ x, data = dat, family = binomial(link = "probit"))
- complimentary log-log
$$log(-log(1-\pi))=\beta_0+\beta_1x_1+\epsilon_i, \hspace{1cm}\epsilon\sim Binom(\lambda)$$
> dat.glmC <- glm(y ~ x, data = dat, family = binomial(link = "cloglog"))
Model evaluation
Prior to exploring the model parameters, it is prudent to confirm that the model did indeed fit the assumptions and was an appropriate fit to the data. There are a number of extractor functions (functions that extract or derive specific information from a model) available including:
| Extractor | Description |
|---|---|
| residuals() | Extracts the residuals from the model |
| fitted() | Extracts the predicted (expected) response values (on the link scale) at the observed levels of the linear predictor |
| predict() | Extracts the predicted (expected) response values (on either the link, response or terms (linear predictor) scale) |
| coef() | Extracts the model coefficients |
| deviance() | Extracts the deviance from the model |
| AIC() | Extracts the Akaike's Information Criterion from the model |
| extractAIC() | Extracts the generalized Akaike's Information Criterion from the model |
| summary() | Summarizes the important output and characteristics of the model |
| anova() | Computes an analysis of deviance or log-likelihood ratio test (LRT) from the model |
| plot() | Generates a series of diagnostic plots from the model |
Lets explore the diagnostics - particularly the residuals
> plot(dat.glmL)
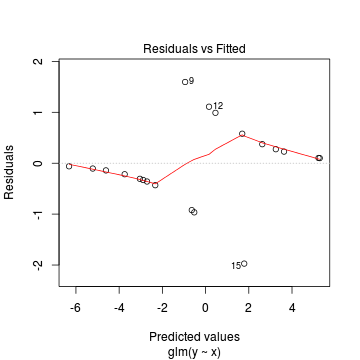

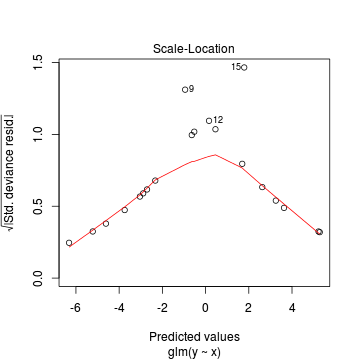
We can also explore the goodness of the fit of the model via:
- Pearson's $\chi^2$ residuals
- explores whether there are any significant patterns remaining in the residuals
> dat.resid <- sum(resid(dat.glmL, type = "pearson")^2) > 1 - pchisq(dat.resid, dat.glmL$df.resid)
[1] 0.8571
- Deviance ($G^2$) - similar to the $chi^2$ test above, yet uses deviance
Conclusions: neither Pearson residuals or Deviance indicate a lack of fit (p values greater than 0.05)> 1 - pchisq(dat.glmL$deviance, dat.glmL$df.resid)
[1] 0.8647
In this demonstration, we fitted three logistic regressions (one for each link function). We could explore the residual plots of each of these for the purpose of comparing fit. We can also compare the fit of each of these three models via AIC (or deviance).
Conclusions: with respect to AIC, they are all essentially identical (although technically the model fit with the probit link function is the best as it has the lowest AIC). Given that they are all very similar, choice comes down to which offers the most appropriate parameter interpretation in the context of the research program. Parameter estimates for the logit model are in log odds ratios.> AIC(dat.glmL, dat.glmP, dat.glmC)
df AIC dat.glmL 2 15.65 dat.glmP 2 15.45 dat.glmC 2 16.11
Exploring the model parameters, test hypotheses
If there was any evidence that the assumptions had been violated or the model was not an appropriate fit, then we would need to reconsider the model and start the process again. In this case, there is no evidence that the test will be unreliable so we can proceed to explore the test statistics. The main statistic of interest is the Wald statistic ($z$) for the slope parameter.
> summary(dat.glmL)
Call: glm(formula = y ~ x, family = "binomial", data = dat) Deviance Residuals: Min 1Q Median 3Q Max -1.9716 -0.3367 -0.0819 0.3004 1.5963 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -6.990 3.160 -2.21 0.027 x 0.656 0.294 2.23 0.025 (Intercept) * x * --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 27.526 on 19 degrees of freedom Residual deviance: 11.651 on 18 degrees of freedom AIC: 15.65 Number of Fisher Scoring iterations: 6Conclusions: We would reject the null hypothesis (p<0.05). An increase in x is associated with a significant linear decline (negative slope) in log odds of $y$ success. Every 1 unit increase in $x$ results in a 0.259 unit decrease in log odds-ratio. We usually express this in terms of odds-ratio rather than log odds-ratio, so every 1 unit increase in $x$ results in a ($e^{0.259}=0.772$) 0.772 unit decline in odds-ratio.
Further explorations of the trends
A measure of the strength of the relationship can be obtained according to: $$quasi R^2 = 1-\left(\frac{deviance}{null~deviance}\right)$$
Conclusions: approximately 49% of the variability in presence/absence can be explained by its relationship to $x$. Technically, it is 49% of the variability in log odds-ratio (the link function) is explained by its relationship to $x$.> 1 - (dat.glmL$deviance/dat.glmL$null)
[1] 0.5767
We might also be interested in the LD50 - the value of $x$ where the probability switches from favoring 1 to favoring 0. LD50 is calculated as: $$LD50 = - \frac{intercept}{slope}$$
Conclusions: the LD50 is 10.66.> -dat.glmL$coef[1]/dat.glmL$coef[2]
(Intercept) 10.66Finally, we will create a summary plot.
> par(mar = c(4, 5, 0, 0)) > plot(y ~ x, data = dat, type = "n", ann = F, axes = F) > points(y ~ x, data = dat, pch = 16) > xs <- seq(0, 20, l = 1000) > ys <- predict(dat.glmL, newdata = data.frame(x = xs), + type = "response", se = T) > points(ys$fit ~ xs, col = "black", type = "l") > lines(ys$fit - 1 * ys$se.fit ~ xs, col = "black", type = "l", + lty = 2) > lines(ys$fit + 1 * ys$se.fit ~ xs, col = "black", type = "l", + lty = 2) > axis(1) > mtext("X", 1, cex = 1.5, line = 3) > axis(2, las = 2) > mtext("Y", 2, cex = 1.5, line = 3) > box(bty = "l")

Grouped binary data
Scenario and Data
In the previous demonstration, the response variable represented the state of a single item per level of the predictor variable ($x$). That single item could be observed having a value of either 1 or 0. Another common situation is to observe the number of items in one of two states (typically dead or alive) for each level of a treatment. For example, you could tally up the number of germinated and non-germinated seeds out of a bank of 10 seeds at each of 8 temperature or nutrient levels.
Recall that the binomial distribution represents the density (probability) of all possible successes (germinations) out of a total of $N$ items (seeds). Hence the binomial distribution is also a suitable error distribution for such grouped binary data.
For this demonstration, we will model the number of successes against a uniformly distributed predictor ($x$). The number of trials in each group (level of the predictor) will vary slightly (yet randomly) so as to mimick complications that inevadably occur in real experimentws.
Random data incorporating the following trends (effect parameters)- the number of levels of $x$ = 10
- the continuous $x$ variable is a random uniform spread of measurements between 10 and 20
- the rate of change in log odds ratio per unit change in x (slope) = -0.25. The magnitude of the slope is an indicator of how abruptly the log odds ratio changes. A very abrupt change would occur if there was very little variability in the trend. That is, a large slope would be indicative of a threshold effect. A lower slope indicates a gradual change in odds ratio and thus a less obvious and precise switch between the likelihood of 1 vs 0.
- the inflection point (point where the slope of the line is greatest) = 10. The inflection point indicates the value of the predictor ($x$) where the log Odds are 50% (switching between 1 being more likely and 0 being more likely). This is also known as the LD50.
- the intercept (which has no real interpretation) is equal to the negative of the slope multiplied by the inflection point
- generate the values of $y$ expected at each $x$ value, we evaluate the linear predictor.
- generate random numbers of trials per group by drawing integers out of a binomial distribution with a total size of 20 and probability of 0.9. Hence the maximum number of trials per group will be 20, yet some will be less than that.
- the number of success per group are drawn from a binomial distribution with a total size equal to the trial sizes generated in the previous step and probabilities equal to the expected $y$ values
- finally, the number of failures per group are calculated as the difference between the total trial size and number of successes per group.
> set.seed(8) > # The number of levels of x > n.x <- 10 > # Create x values that at uniformly distributed > # throughout the rate of 10 to 20 > x <- sort(runif(n = n.x, min = 10, max = 20)) > # The slope is the rate of change in log odds ratio > # for each unit change in x the smaller the slope, > # the slower the change (more variability in data > # too) > slope = -0.25 > # Inflection point is where the slope of the line > # is greatest this is also the LD50 point > inflect <- 15 > # Intercept (no interpretation) > intercept <- -1 * (slope * inflect) > # The linear predictor > linpred <- intercept + slope * x > # Predicted y values > y.pred <- exp(linpred)/(1 + exp(linpred)) > # Add some noise and make binary (0's and 1's) > n.trial <- rbinom(n = n.x, 20, prob = 0.9) > success <- rbinom(n = n.x, size = n.trial, prob = y.pred) > failure <- n.trial - success > dat <- data.frame(success, failure, x)
Exploratory data analysis and initial assumption checking
The assumptions are:- All of the observations are independent - this must be addressed at the design and collection stages
- The response variable (and thus the residuals) should be matched by an appropriate distribution (in the case of a binary response - a binomial is appropriate).
- All observations are equally influential in determining the trends - or at least no observations are overly influential. This is most effectively diagnosed via residuals and other influence indices and is very difficult to diagnose prior to analysis
- the relationship between the linear predictor (right hand side of the regression formula) and the link function should be linear. A scatterplot with smoother can be useful for identifying possible non-linearity.
So lets explore linearity by creating a histogram of the predictor variable ($x$) and a scatterplot of the relationship between the either the number of successes ($success$) or the number of ($failures$) and the predictor ($x$). Note, that this will not account for the differences in trial size per group and so a scatterplot of the relationship between the number of successes ($success$) or the number of ($failures$) divided by the total number of trials against the predictor ($x$) might be more appropriate.
> hist(dat$x)

> # now for the scatterplot > plot(success ~ x, dat) > with(dat, lines(lowess(success ~ x)))

> # scatterplot standardized for trial size > plot(success/(success + failure) ~ x, dat) > with(dat, lines(lowess(success/(success + failure) ~ + x)))

Conclusions: the predictor ($x$) does not display any skewness (although it is not all that uniform - random data hey!) or other issues that might lead to non-linearity. The lowess smoother on either scatterplot does not display major deviations from a standard sigmoidal curve and thus linearity is likely to be satisfied. Violations of linearity could be addressed by either:
- define a non-linear linear predictor (such as a polynomial, spline or other non-linear function)
- transform the scale of the predictor variables
Model fitting or statistical analysis
We perform the logistic regression using the glm() function. Clearly the number of successes is also dependent on the number of trials. Larger numbers of trials might be expected to yeild higher numbers of successes. Model weights can be used to account for differences in the total numbers of trials within each group. The most important (=commonly used) parameters/arguments for logistic regression are:
- formula: the linear model relating the response variable to the linear predictor
- family: specification of the error distribution (and link function). Can be specified as either a string or as one of the family functions (which allows for the explicit declaration of the link function).
For examples:
- family="binomial" or equivalently family=binomial(link="logit")
- family=binomial(link="probit")
- data: the data frame containing the data
- weights: vector of weights to be used in the fitting process. These are particularly useful when dealing with grouped binary data from unequal sample sizes.
I will demonstrate logistic regression with a range of possible link functions (each of which yield different parameter interpretations):
- logit
$$log\left(\frac{\pi}{1-\pi}\right)=\beta_0+\beta_1x_1+\epsilon_i, \hspace{1cm}\epsilon\sim Binom(\lambda)$$
> dat <- within(dat, total <- success + failure) > dat.glmL <- glm(cbind(success, failure) ~ x, data = dat, + family = "binomial", weight = total)
- probit
$$\phi^{-1}\left(\pi\right)=\beta_0+\beta_1x_1+\epsilon_i, \hspace{1cm}\epsilon\sim Binom(\lambda)$$
> dat.glmP <- glm(cbind(success, failure) ~ x, data = dat, + family = binomial(link = "probit"), weight = total)
- complimentary log-log
$$log(-log(1-\pi))=\beta_0+\beta_1x_1+\epsilon_i, \hspace{1cm}\epsilon\sim Binom(\lambda)$$
> dat.glmC <- glm(cbind(success, failure) ~ x, data = dat, + family = binomial(link = "cloglog"), weight = total)
Model evaluation
Prior to exploring the model parameters, it is prudent to confirm that the model did indeed fit the assumptions and was an appropriate fit to the data.
Lets explore the diagnostics - particularly the residuals
Conclusions: there is no obvious patterns in the residuals, or at least there are no obvious trends remaining that would be indicative of non-linearity.> plot(resid(dat.glmL) ~ fitted(dat.glmL)) > lines(lowess(resid(dat.glmL) ~ fitted(dat.glmL)))

In this demonstration, we fitted three logistic regressions (one for each link function). We could explore the residual plots of each of these for the purpose of comparing fit. We can also compare the fit of each of these three models via AIC (or deviance).
Conclusions: with respect to AIC, they are all essentially identical (although technically the model fit with the complimentary log-log link function is the best as it has the lowest AIC). Given that they are all very similar, choice comes down to which offers the most appropriate parameter interpretation in the context of the research program. Parameter estimates for the logit model are in log odds ratios.> AIC(dat.glmL, dat.glmP, dat.glmC)
df AIC dat.glmL 2 716.2 dat.glmP 2 716.3 dat.glmC 2 715.2
Exploring the model parameters, test hypotheses
If there was any evidence that the assumptions had been violated or the model was not an appropriate fit, then we would need to reconsider the model and start the process again. In this case, there is no evidence that the test will be unreliable so we can proceed to explore the test statistics. The main statistic of interest is the Wald statistic ($z$) for the slope parameter.
> summary(dat.glmL)
Call: glm(formula = cbind(success, failure) ~ x, family = "binomial", data = dat, weights = total) Deviance Residuals: Min 1Q Median 3Q Max -6.31 -1.25 0.50 2.12 5.88 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 4.0472 0.2525 16.0 <2e-16 x -0.2591 0.0158 -16.4 <2e-16 (Intercept) *** x *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 394.60 on 9 degrees of freedom Residual deviance: 105.33 on 8 degrees of freedom AIC: 716.2 Number of Fisher Scoring iterations: 3Conclusions: We would reject the null hypothesis (p<0.05). An increase in x is associated with a significant linear increase (positive slope) in log odds of $y$ presence (assuming a $y$ value of 1 indicates present). Every 1 unit increase in $x$ results in a 0.66 unit increase in log odds-ratio. We usually express this in terms of odds-ratio rather than log odds-ratio, so every 1 unit increase in $x$ results in a ($e^{0.656}=1.93$) 1.93 unit increase in odds-ratio.
Further explorations of the trends
A measure of the strength of the relationship can be obtained according to: $$quasi R^2 = 1-\left(\frac{deviance}{null~deviance}\right)$$
Conclusions: approximately 73% of the variability in presence/absence can be explained by its relationship to $x$. Technically, it is 73% of the variability in log odds-ratio (the link function) is explained by its relationship to $x$.> 1 - (dat.glmL$deviance/dat.glmL$null)
[1] 0.7331
We might also be interested in the LD50 - the value of $x$ where the probability switches from favoring 1 to favoring 0. LD50 is calculated as: $$LD50 = - \frac{intercept}{slope}$$
Conclusions: the LD50 is 15.62. This is the value of $x$ where the probability of success is exactly 50%.> -dat.glmL$coef[1]/dat.glmL$coef[2]
(Intercept) 15.62Finally, we will create a summary plot.
> par(mar = c(4, 5, 0, 0)) > plot(success/(success + failure) ~ x, data = dat, type = "n", + ann = F, axes = F) > points(success/(success + failure) ~ x, data = dat, + pch = 16) > xs <- seq(10, 20, l = 1000) > ys <- predict(dat.glmL, newdata = data.frame(x = xs), + type = "response", se = T) > points(ys$fit ~ xs, col = "black", type = "l") > lines(ys$fit - 2 * ys$se.fit ~ xs, col = "black", type = "l", + lty = 2) > lines(ys$fit + 2 * ys$se.fit ~ xs, col = "black", type = "l", + lty = 2) > axis(1) > mtext("X", 1, cex = 1.5, line = 3) > axis(2, las = 2) > mtext("Probability of success", 2, cex = 1.5, line = 3) > box(bty = "l")

- Deviance ($G^2$) - similar to the $chi^2$ test above, yet uses deviance
