Workshop 9.2a: Nested designs

Murray Logan

23 Nov 2016

Nested designs

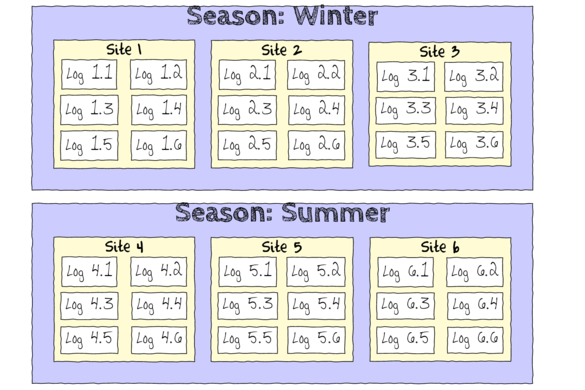
Nested design

Simple

Nested

Nested design

> data.nest <- read.csv('../data/data.nest.csv')
> head(data.nest)
         y Region Sites Quads
1 32.25789      A    S1     1
2 32.40160      A    S1     2
3 37.20174      A    S1     3
4 36.58866      A    S1     4
5 35.45206      A    S1     5
6 37.07744      A    S1     6

Nested design

> library(ggplot2)
> data.nest$Sites <- factor(data.nest$Sites, levels=paste0('S',1:nSites))
> ggplot(data.nest, aes(y=y, x=1,color=Region)) + geom_boxplot() +
+     facet_grid(.~Sites) +
+     scale_x_continuous('', breaks=NULL)+theme_classic()

Nested design

> #Effects of treatment
> library(plyr)
> boxplot(y~Region, ddply(data.nest, ~Region+Sites,
+                         numcolwise(mean, na.rm=T)))

Nested design

> #Site effects
> boxplot(y~Sites, ddply(data.nest, ~Region+Sites+Quads,
+                        numcolwise(mean, na.rm=T)))

Nested design

\(y = \mu + \alpha + \beta(\alpha) + \epsilon\)

e.g.

\(abundance = base + burnt + quadrat(burnt)\)

Nested design

\(y = \mu + \alpha + \beta(\alpha) + \epsilon\\ y_{ijk} = \mu + \alpha_{i}{}Region_i + \beta_{j(i)}Sites_{j(i)} + \epsilon_{ijk}\)

\(\mu\) - base (mean of first Region)

\(\alpha\) - main fixed effect

\(\beta\) - sub-replicates (Sites: random effect)

> with(data.nest, table(Region,Sites))
      Sites
Region S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 S12 S13 S14 S15
     A 10 10 10 10 10  0  0  0  0   0   0   0   0   0   0
     B  0  0  0  0  0 10 10 10 10  10   0   0   0   0   0
     C  0  0  0  0  0  0  0  0  0   0  10  10  10  10  10
> head(data.nest, 20)
          y Region Sites Quads
1  32.25789      A    S1     1
2  32.40160      A    S1     2
3  37.20174      A    S1     3
4  36.58866      A    S1     4
5  35.45206      A    S1     5
6  37.07744      A    S1     6
7  36.39324      A    S1     7
8  32.85538      A    S1     8
9  22.53580      A    S1     9
10 35.58168      A    S1    10
11 41.92308      A    S2    11
12 41.42474      A    S2    12
13 34.84996      A    S2    13
14 39.81297      A    S2    14
15 44.29343      A    S2    15
16 48.99712      A    S2    16
17 41.68978      A    S2    17
18 44.14208      A    S2    18
19 41.93469      A    S2    19
20 35.31842      A    S2    20

Nested design

\(y = \mu + \alpha + \beta(\alpha) + \epsilon\\ y_{ijk} = \mu + \alpha_{i}{}Region_i + \beta_{j(i)}Sites_{j(i)} + \epsilon_{ijk}\) 
> library(nlme)
> data.nest.lme <- lme(y~Region, random=~1|Sites, data.nest)
> plot(data.nest.lme)

Nested design

> plot(data.nest$Region, residuals(data.nest.lme,
+       type='normalized'))

Nested design

> summary(data.nest.lme)
Linear mixed-effects model fit by REML
 Data: data.nest 
       AIC      BIC    logLik
  927.7266 942.6788 -458.8633

Random effects:
 Formula: ~1 | Sites
        (Intercept) Residual
StdDev:     13.6582 4.372252

Fixed effects: y ~ Region 
               Value Std.Error  DF  t-value p-value
(Intercept) 42.27936  6.139350 135 6.886618  0.0000
RegionB     29.84692  8.682352  12 3.437654  0.0049
RegionC     37.02026  8.682352  12 4.263851  0.0011
 Correlation: 
        (Intr) ReginB
RegionB -0.707       
RegionC -0.707  0.500

Standardized Within-Group Residuals:
         Min           Q1          Med           Q3          Max 
-2.603787242 -0.572951701  0.004953998  0.620914933  2.765601716 

Number of Observations: 150
Number of Groups: 15

Nested design

> VarCorr(data.nest.lme)
Sites = pdLogChol(1) 
            Variance  StdDev   
(Intercept) 186.54644 13.658200
Residual     19.11659  4.372252
> anova(data.nest.lme)
            numDF denDF  F-value p-value
(Intercept)     1   135 331.8308  <.0001
Region          2    12  10.2268  0.0026

Nested design

> library(multcomp)
> summary(glht(data.nest.lme, linfct=mcp(Region="Tukey")))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lme.formula(fixed = y ~ Region, data = data.nest, random = ~1 | 
    Sites)

Linear Hypotheses:
           Estimate Std. Error z value Pr(>|z|)    
B - A == 0   29.847      8.682   3.438  0.00172 ** 
C - A == 0   37.020      8.682   4.264  < 0.001 ***
C - B == 0    7.173      8.682   0.826  0.68674    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

Nested design

> library(effects)
> plot(allEffects(data.nest.lme))

Linear mixed effects model

Summary figure

Step 1. gather model coefficients and model matrix

> coefs <- fixef(data.nest.lme)
> coefs
(Intercept)     RegionB     RegionC 
   42.27936    29.84692    37.02026 
> xs <- levels(data.nest$Region)
> Xmat <- model.matrix(~Region, data.frame(Region=xs))
> head(Xmat)
  (Intercept) RegionB RegionC
1           1       0       0
2           1       1       0
3           1       0       1

Linear mixed effects model

Summary figure

Step 3. calculate predicted y and CI

> ys <- t(coefs %*% t(Xmat))
> head(ys)
      [,1]
1 42.27936
2 72.12628
3 79.29961
> SE <- sqrt(diag(Xmat %*% vcov(data.nest.lme) %*% t(Xmat)))
> CI <- 2*SE
> #OR
> CI <- qt(0.975,length(data.nest$y)-2)*SE
> data.nest.pred <- data.frame(Region=xs, fit=ys, se=SE,
+      lower=ys-CI, upper=ys+CI)
> head(data.nest.pred)
  Region      fit      se    lower    upper
1      A 42.27936 6.13935 30.14725 54.41147
2      B 72.12628 6.13935 59.99417 84.25839
3      C 79.29961 6.13935 67.16751 91.43172

Linear mixed effects model

Summary figure

Step 4. plot it

> with(data.nest.pred,plot.default(Region, fit,type='n',axes=F, ann=F,ylim=range(c(data.nest.pred$lower, data.nest.pred$upper))))
> points(y~Region, data=data.nest, pch=16, col='grey')
> points(fit~Region, data=data.nest.pred, pch=16)
> with(data.nest.pred, arrows(as.numeric(Region),lower,as.numeric(Region),upper, length=0.1, angle=90, code=3))
> axis(1, at=1:3, labels=levels(data.nest$Region))
> mtext('Region',1,line=3)
> axis(2,las=1)
> mtext('Y',2,line=3)
> box(bty='l')

Linear mixed effects model

Summary figure

Linear mixed effects model

Summary figure

Step 4. plot it

> data.nest$res <- predict(data.nest.lme, level=0)-
+     residuals(data.nest.lme)
> with(data.nest.pred,plot.default(Region, fit,type='n',axes=F, ann=F,ylim=range(c(data.nest.pred$lower, data.nest.pred$upper))))
> points(res~Region, data=data.nest, pch=16, col='grey')
> points(fit~Region, data=data.nest.pred, pch=16)
> with(data.nest.pred, arrows(as.numeric(Region),lower,as.numeric(Region),upper, length=0.1, angle=90, code=3))
> axis(1, at=1:3, labels=levels(data.nest$Region))
> mtext('Region',1,line=3)
> axis(2,las=1)
> mtext('Y',2,line=3)
> box(bty='l')

Linear mixed effects model

Summary figure

Linear mixed effects model

> library(ggplot2)
> data.nest$res <- predict(data.nest.lme, level=0)-
+     residuals(data.nest.lme)
> 
> ggplot(data.nest.pred, aes(y=fit, x=Region))+
+     geom_point(data=data.nest, aes(y=res), col='grey',position = position_jitter(height=0))+
+     geom_errorbar(aes(ymin=lower, ymax=upper), width=0.1)+     
+     geom_point()+
+     theme_classic()+
+     theme(axis.title.y=element_text(vjust=2),
+           axis.title.x=element_text(vjust=-1))

Linear mixed effects model

Worked Examples

Worked Examples

Format of curdies.csv data files
SEASON SITE DUGESIA S4DUGESIA
WINTER 1 0.648 0.897
.. .. .. ..
WINTER 2 1.016 1.004
.. .. .. ..
WINTER 3 0.689 0.991
.. .. .. ..
SUMMER 4 0 0
.. .. .. ..

Each row represents a different stone
SEASON Season in which flatworms were counted - fixed factor
SITE Site from where flatworms were counted - nested within SEASON (random factor)
DUGESIA Number of flatworms counted on a particular stone
S4DUGESIA 4th root transformation of DUGESIA variable
Dugesia

Worked Examples