Workshop 9.15.3a: Mixed effects models

Murray Logan

22-09-2014

Linear models

\[ \begin{align*} y_{i} &= \beta_0 + \beta_1 \times x_{i} + \varepsilon_i\\ \epsilon_i&\sim\mathcal{N}(0, \sigma^2) \\ \end{align*} \]

Linear models

Linear models

Linear models

Linear models

Hierarchical models

Linear modelling assumptions

\[ \begin{align*} y_{i} &= \beta_0 + \beta_1 \times x_{i} + \varepsilon_i\\ \epsilon_i&\sim\mathcal{N}(0, \sigma^2) \\ \end{align*} \]

Non-independence

Hierarchical models

Example

data.rcb <- read.csv('../data/data.rcb.csv')
head(data.rcb)
      y     x  block
1 281.1 18.59 Block1
2 295.7 26.05 Block1
3 328.3 40.10 Block1
4 360.2 63.57 Block1
5 276.7 14.12 Block1
6 349.0 62.89 Block1
library(car)
scatterplot(y~x, data.rcb)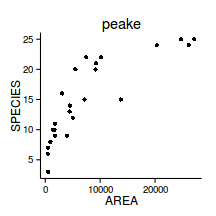

Example

ggplot(data.rcb, aes(y=y, x=x,color=block))+geom_point()+
    geom_smooth(method='lm')
Error: could not find function "ggplot"

Example

Simple linear regression - wrong

data.rcb.lm <- lm(y~x, data.rcb)


Generalized least squares - more correct

library(nlme)
data.rcb.gls <- gls(y~x, data.rcb, method='REML')

Example

Model validation

plot(data.rcb.gls)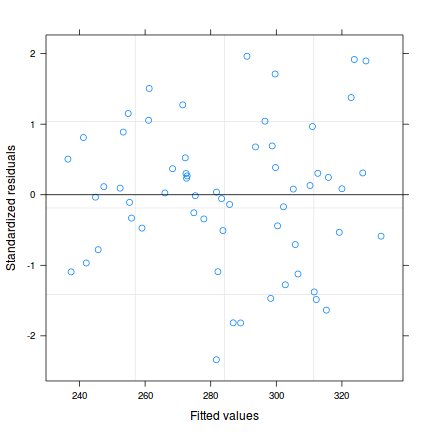

Example

plot(residuals(data.rcb.gls, type='normalized') ~
     data.rcb$block)


- So what about ANCOVA

Example

library(ggplot2)
ggplot(data.rcb, aes(y=y, x=x, color=block))+
    geom_smooth(method="lm")+geom_point()+theme_classic()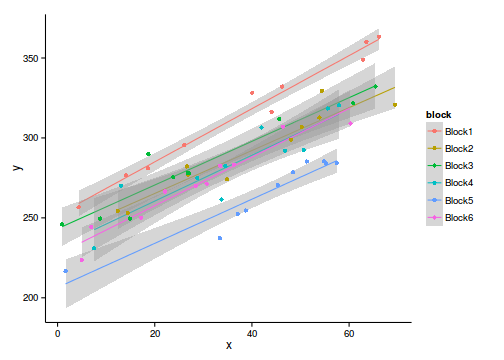
ggplot(data.rcb, aes(y=y, x=x))+
    geom_smooth(method="lm")+geom_point()+theme_classic()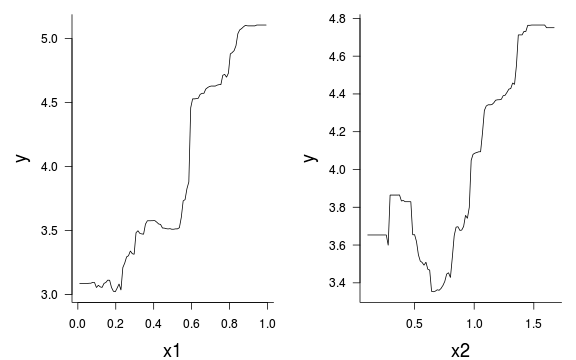

Example

library(nlme)
data.rcb.gls1 <- gls(y~x+block, data.rcb, method='REML')
plot(data.rcb.gls)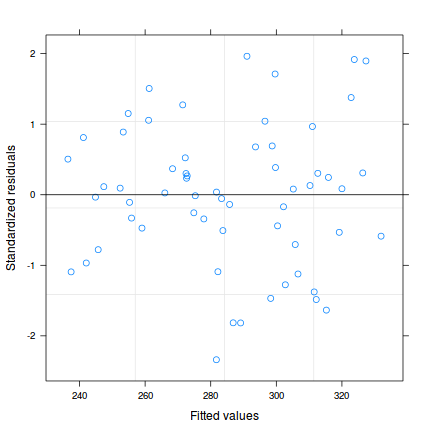

Example

plot(residuals(data.rcb.gls1, type='normalized') ~
     data.rcb$block)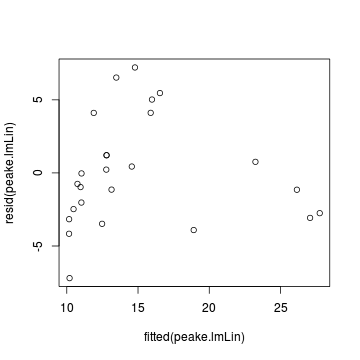


Example



Example

library(nlme)
data.rcb.gls2<-gls(y~x,data.rcb,
                   correlation=corCompSymm(form=~1|block),
                   method="REML")
plot(residuals(data.rcb.gls2, type='normalized') ~
     fitted(data.rcb.gls2))

Example

plot(residuals(data.rcb.gls2, type='normalized') ~
     data.rcb$block)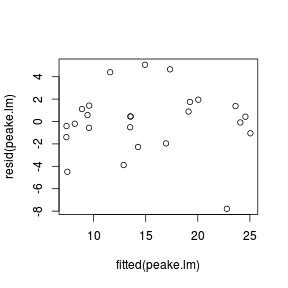

Example

summary(data.rcb.gls2)
Generalized least squares fit by REML
  Model: y ~ x 
  Data: data.rcb 
  AIC   BIC logLik
  459 467.2 -225.5

Correlation Structure: Compound symmetry
 Formula: ~1 | block 
 Parameter estimate(s):
   Rho 
0.8053 

Coefficients:
             Value Std.Error t-value p-value
(Intercept) 232.82     7.823   29.76       0
x             1.46     0.064   22.87       0

 Correlation: 
  (Intr)
x -0.292

Standardized residuals:
     Min       Q1      Med       Q3      Max 
-2.19175 -0.59481  0.05261  0.59571  1.83322 

Residual standard error: 20.18 
Degrees of freedom: 60 total; 58 residual

Linear mixed effects model

data.rcb.lm <- lm(y~x, data.rcb)
plot(rstandard(data.rcb.lm) ~ fitted(data.rcb.lm))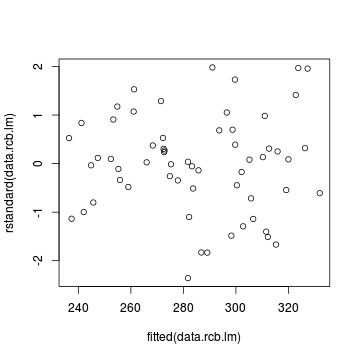
plot(rstandard(data.rcb.lm) ~ data.rcb$block)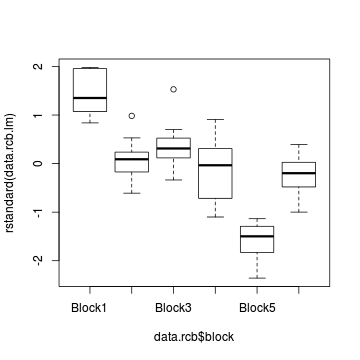
data.rcb.lme <- lme(y~x, random=~1|block, data.rcb,
                    method='REML')
plot(data.rcb.lme)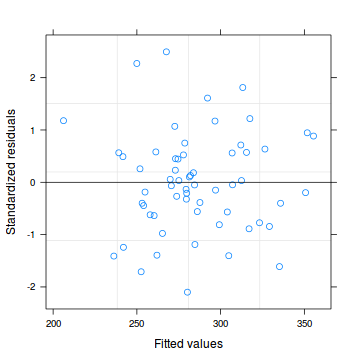
plot(residuals(data.rcb.lme, type='normalized') ~ fitted(data.rcb.lme))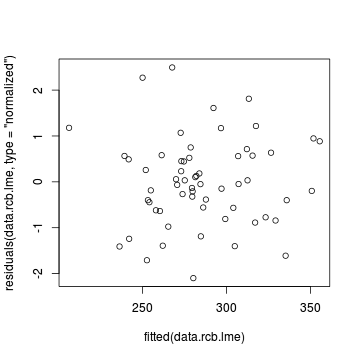
plot(residuals(data.rcb.lme, type='normalized') ~ data.rcb$block)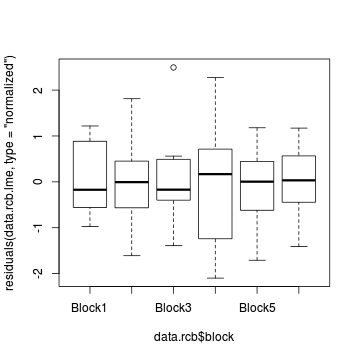

Linear mixed effects model

summary(data.rcb.lme)
Linear mixed-effects model fit by REML
 Data: data.rcb 
  AIC   BIC logLik
  459 467.2 -225.5

Random effects:
 Formula: ~1 | block
        (Intercept) Residual
StdDev:       18.11    8.905

Fixed effects: y ~ x 
             Value Std.Error DF t-value p-value
(Intercept) 232.82     7.823 53   29.76       0
x             1.46     0.064 53   22.87       0
 Correlation: 
  (Intr)
x -0.292

Standardized Within-Group Residuals:
     Min       Q1      Med       Q3      Max 
-2.09947 -0.57994 -0.04874  0.56685  2.49464 

Number of Observations: 60
Number of Groups: 6

Linear mixed effects model

anova(data.rcb.lme)
            numDF denDF F-value p-value
(Intercept)     1    53  1452.3  <.0001
x               1    53   523.2  <.0001
intervals(data.rcb.lme)
Approximate 95% confidence intervals

 Fixed effects:
              lower    est.   upper
(Intercept) 217.128 232.819 248.511
x             1.331   1.459   1.587
attr(,"label")
[1] "Fixed effects:"

 Random Effects:
  Level: block 
                lower  est. upper
sd((Intercept)) 9.598 18.11 34.17

 Within-group standard error:
 lower   est.  upper 
 7.362  8.905 10.773

Linear mixed effects model

vc<-as.numeric(as.matrix(VarCorr(data.rcb.lme))[,1])
vc/sum(vc)
[1] 0.8052 0.1948

Linear mixed effects model

library(effects)
plot(allEffects(data.rcb.lme))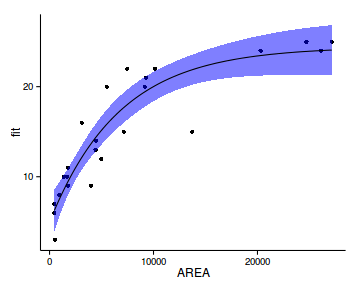

Linear mixed effects model

predict(data.rcb.lme, newdata=data.frame(x=30:40),level=0)
 [1] 276.6 278.1 279.5 281.0 282.4 283.9 285.3
 [8] 286.8 288.3 289.7 291.2
attr(,"label")
[1] "Predicted values"

Linear mixed effects model

predict(data.rcb.lme, newdata=data.frame(x=30:40,
                          block='Block1'),level=1)
Block1 Block1 Block1 Block1 Block1 Block1 Block1 
 302.7  304.2  305.7  307.1  308.6  310.0  311.5 
Block1 Block1 Block1 Block1 
 313.0  314.4  315.9  317.3 
attr(,"label")
[1] "Predicted values"

Linear mixed effects model

Summary figure

Step 1. gather model coefficients

coefs <- fixef(data.rcb.lme)
coefs
(Intercept)           x 
    232.819       1.459

Linear mixed effects model

Summary figure

Step 2. generate prediction model matrix

xs <- seq(min(data.rcb$x), max(data.rcb$x), l=100)
Xmat <- model.matrix(~x, data.frame(x=xs))
head(Xmat)
  (Intercept)      x
1           1 0.9373
2           1 1.6292
3           1 2.3211
4           1 3.0130
5           1 3.7048
6           1 4.3967

Linear mixed effects model

Summary figure

Step 3. calculate predicted y

ys <- t(coefs %*% t(Xmat))
head(ys)
   [,1]
1 234.2
2 235.2
3 236.2
4 237.2
5 238.2
6 239.2

Linear mixed effects model

Summary figure

Step 3. calculate confidence interval

SE <- sqrt(diag(Xmat %*% vcov(data.rcb.lme) %*% t(Xmat)))
CI <- 2*SE
#OR
CI <- qt(0.975,length(data.rcb$x)-2)*SE
data.rcb.pred <- data.frame(x=xs, fit=ys, se=SE,
     lower=ys-CI, upper=ys+CI)
head(data.rcb.pred)
       x   fit    se lower upper
1 0.9373 234.2 7.806 218.6 249.8
2 1.6292 235.2 7.794 219.6 250.8
3 2.3211 236.2 7.781 220.6 251.8
4 3.0130 237.2 7.769 221.7 252.8
5 3.7048 238.2 7.758 222.7 253.8
6 4.3967 239.2 7.746 223.7 254.7

Linear mixed effects model

Summary figure

Step 4. plot it

plot(fit~x, data=data.rcb.pred,type='n',axes=F, ann=F)
points(y~x, data=data.rcb, pch=16, col='grey')
with(data.rcb.pred, polygon(c(x,rev(x)), c(lower, rev(upper)),
         col="#0000FF50",border=FALSE))
lines(fit~x,data=data.rcb.pred)
lines(lower~x,data=data.rcb.pred, lty=2)
lines(upper~x,data=data.rcb.pred, lty=2)
axis(1)
mtext('X',1,line=3)
axis(2,las=1)
mtext('Y',2,line=3)
box(bty='l')

Linear mixed effects model

Summary figure

Linear mixed effects model

Summary figure

Step 4. plot it

data.rcb$res <- predict(data.rcb.lme, level=0)-
    residuals(data.rcb.lme)
plot(fit~x, data=data.rcb.pred,type='n',axes=F, ann=F)
points(res~x, data=data.rcb, pch=16, col='grey')
with(data.rcb.pred, polygon(c(x,rev(x)), c(lower, rev(upper)),
         col="#0000FF50",border=FALSE))
lines(fit~x,data=data.rcb.pred)
lines(lower~x,data=data.rcb.pred, lty=2)
lines(upper~x,data=data.rcb.pred, lty=2)
axis(1)
mtext('X',1,line=3)
axis(2,las=1)
mtext('Y',2,line=3)
box(bty='l')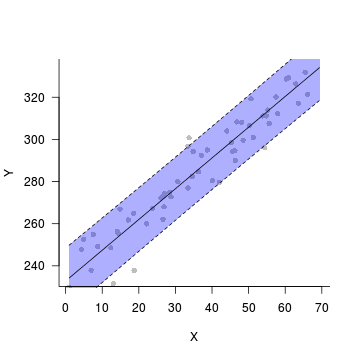

Linear mixed effects model

Summary figure

Linear mixed effects model

library(ggplot2)
data.rcb$res <- predict(data.rcb.lme, level=0)+
    residuals(data.rcb.lme)

ggplot(data.rcb.pred, aes(y=fit, x=x))+
    geom_point(data=data.rcb, aes(y=res), col='grey')+
    geom_ribbon(aes(ymin=lower, ymax=upper),
                fill='blue', alpha=0.2)+
    geom_line()+
    theme_classic()+
    theme(axis.title.y=element_text(vjust=2),
          axis.title.x=element_text(vjust=-1))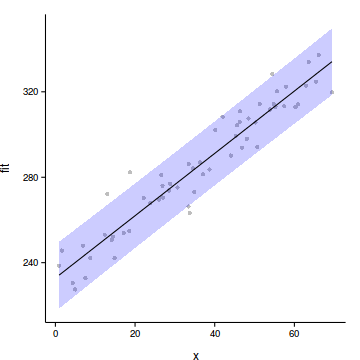

Linear mixed effects model

Bayesian HMM

modelString = '
model{
   for (i in 1:n) {
     y[i] ~ dnorm(mu[i], tau)
     mu[i] <- beta.blk[block[i]] + alpha + beta*x[i]
   }
   alpha ~ dnorm(0,1.0E-06)
   beta ~ dnorm(0,1.0E-06)
   for (i in 1:nBlock) {
     beta.blk[i] ~ dnorm(0, tau.blk)
   }
   tau <- 1/(sigma * sigma)
   tau.blk <- 1/(sigma.blk * sigma.blk)
   sigma ~ dunif(0,1000)
   sigma.blk ~ dunif(0,1000)
}
'
writeLines(modelString, con='HMM.jags')
library(R2jags)

data.list <- with(data.rcb, list(y=y, x=x,
          block=as.numeric(block),
          n=nrow(data.rcb),
          nBlock=length(unique(block))
                  ))

data.rcb.jags <- jags(data=data.list, inits=NULL,
                      param = c('alpha','beta','beta.blk','sigma','sigma.blk'),
                      model.file = 'HMM.jags',
                      n.chains=3, n.iter=20000, n.burnin = 10000,
                      n.thin=10)
Compiling model graph
   Resolving undeclared variables
   Allocating nodes
   Graph Size: 320

Initializing model
print(data.rcb.jags)
Inference for Bugs model at "HMM.jags", fit using jags,
 3 chains, each with 20000 iterations (first 10000 discarded), n.thin = 10
 n.sims = 3000 iterations saved
            mu.vect sd.vect    2.5%     25%
alpha       233.017  12.408 208.482 226.390
beta          1.460   0.066   1.331   1.416
beta.blk[1]  26.029  12.470   0.851  19.397
beta.blk[2]   0.822  12.415 -24.059  -5.842
beta.blk[3]   7.276  12.461 -17.742   0.613
beta.blk[4]  -2.076  12.419 -26.452  -8.752
beta.blk[5] -29.259  12.346 -55.191 -35.653
beta.blk[6]  -3.979  12.413 -28.779 -10.533
sigma         9.139   0.905   7.601   8.495
sigma.blk    26.062  14.997  12.056  17.570
deviance    434.129   4.324 427.692 430.899
                50%     75%   97.5%  Rhat n.eff
alpha       233.062 239.456 257.772 1.002  3000
beta          1.460   1.505   1.586 1.001  2400
beta.blk[1]  26.023  32.627  51.147 1.003  1900
beta.blk[2]   0.916   7.619  25.225 1.003  2700
beta.blk[3]   7.336  14.138  30.461 1.003  1900
beta.blk[4]  -1.995   4.644  22.392 1.004  3000
beta.blk[5] -29.161 -22.484  -5.543 1.004  3000
beta.blk[6]  -3.801   2.796  19.772 1.003  1800
sigma         9.076   9.708  11.055 1.002  1800
sigma.blk    22.466  29.756  62.270 1.002  3000
deviance    433.502 436.588 444.495 1.001  3000

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = var(deviance)/2)
pD = 9.4 and DIC = 443.5
DIC is an estimate of expected predictive error (lower deviance is better).

Bayesian HMM

modelString = '
model{
   for (i in 1:n) {
     y[i] ~ dnorm(mu[i], tau)
     mu[i] <- beta.blk[block[i]] + alpha + beta*x[i]
     res[i] <- y[i]-mu[i]
   }
   alpha ~ dnorm(0,1.0E-06)
   beta ~ dnorm(0,1.0E-06)
   for (i in 1:nBlock) {
     beta.blk[i] ~ dnorm(0, tau.blk)
   }
   tau <- 1/(sigma * sigma)
   tau.blk <- 1/(sigma.blk * sigma.blk)
   sigma ~ dunif(0,1000)
   sigma.blk ~ dunif(0,1000)

   sd.res <- sd(res[])
   sd.x <-abs(beta)*sd(x[])
   sd.blk <- sd(beta.blk[])
}
'
writeLines(modelString, con='HMM1.jags')
library(R2jags)

data.list <- with(data.rcb, list(y=y, x=x,
          block=as.numeric(block),
          n=nrow(data.rcb),
          nBlock=length(unique(block))
                  ))

data.rcb.jags <- jags(data=data.list, inits=NULL,
                      param = c('alpha','beta','beta.blk','sigma','sigma.blk','sd.res','sd.x','sd.blk','res'),
                      model.file = 'HMM1.jags',
                      n.chains=3, n.iter=20000, n.burnin = 10000,
                      n.thin=10)
Compiling model graph
   Resolving undeclared variables
   Allocating nodes
   Graph Size: 388

Initializing model
print(data.rcb.jags)
Inference for Bugs model at "HMM1.jags", fit using jags,
 3 chains, each with 20000 iterations (first 10000 discarded), n.thin = 10
 n.sims = 3000 iterations saved
            mu.vect sd.vect    2.5%     25%
alpha       232.468  11.955 207.386 225.958
beta          1.462   0.065   1.332   1.418
beta.blk[1]  26.538  11.951   4.472  19.772
beta.blk[2]   1.167  11.840 -21.593  -5.557
beta.blk[3]   7.805  11.909 -14.929   1.236
beta.blk[4]  -1.521  11.835 -24.031  -8.017
beta.blk[5] -28.825  11.930 -52.010 -35.631
beta.blk[6]  -3.508  11.868 -25.906 -10.339
res[1]       -5.069   3.230 -11.486  -7.206
res[2]       -1.436   3.059  -7.546  -3.420
res[3]       10.692   2.936   4.874   8.776
res[4]        8.215   3.342   1.452   6.037
res[5]       -2.941   3.363  -9.640  -5.167
res[6]       -1.976   3.320  -8.686  -4.151
res[7]        7.650   3.425   0.669   5.434
res[8]        5.492   2.971  -0.393   3.587
res[9]       -7.047   2.952 -12.871  -8.970
res[10]      -8.743   3.718 -16.092 -11.160
res[11]      -1.497   3.314  -7.903  -3.761
res[12]       2.464   3.379  -4.091   0.165
res[13]      -4.987   2.991 -10.778  -7.011
res[14]       4.142   3.016  -1.789   2.085
res[15]       0.338   3.095  -5.641  -1.753
res[16]     -10.488   2.930 -16.189 -12.441
res[17]      -0.371   3.024  -6.188  -2.411
res[18]     -14.346   3.563 -21.224 -16.720
res[19]       9.650   3.020   3.703   7.578
res[20]      16.181   3.107  10.133  14.098
res[21]      -3.706   3.778 -10.998  -6.384
res[22]     -12.397   3.068 -18.211 -14.387
res[23]       4.911   3.123  -1.164   2.850
res[24]      -3.536   3.210  -9.683  -5.653
res[25]      22.207   3.001  16.521  20.233
res[26]      -1.885   2.928  -7.556  -3.806
res[27]       4.413   3.453  -2.272   2.160
res[28]      -1.222   2.929  -6.895  -3.133
res[29]      -7.639   3.597 -14.517 -10.155
res[30]       0.274   2.945  -5.442  -1.667
res[31]     -18.790   2.939 -24.512 -20.720
res[32]      14.227   2.931   8.490  12.317
res[33]       0.822   2.934  -4.921  -1.113
res[34]      20.198   3.365  13.723  17.982
res[35]       4.933   3.187  -1.476   2.798
res[36]      -7.344   2.973 -13.255  -9.298
res[37]       6.197   3.130  -0.068   4.102
res[38]     -11.077   3.556 -17.979 -13.447
res[39]     -12.634   3.029 -18.744 -14.619
res[40]       1.985   2.991  -3.821   0.031
res[41]      -3.433   3.131  -9.645  -5.478
res[42]       0.548   2.955  -5.219  -1.418
res[43]       1.642   3.076  -4.371  -0.340
res[44]      -5.608   2.946 -11.335  -7.602
res[45]      -5.462   2.954 -11.192  -7.423
res[46]      -0.436   3.084  -6.492  -2.432
res[47]      10.659   3.917   2.920   7.978
res[48]     -15.150   2.985 -20.943 -17.110
res[49]       6.703   3.016   0.772   4.772
res[50]       3.988   2.982  -1.918   2.044
res[51]       4.641   2.877  -0.992   2.737
res[52]      -8.011   3.481 -14.854 -10.333
res[53]      -2.395   2.869  -7.988  -4.292
res[54]      -3.938   2.994  -9.864  -5.840
res[55]     -12.497   3.311 -18.846 -14.683
res[56]       5.083   3.247  -1.227   2.966
res[57]       5.185   2.917  -0.581   3.313
res[58]       1.121   2.897  -4.500  -0.804
res[59]      10.369   3.058   4.320   8.288
res[60]      -0.593   2.871  -6.207  -2.482
sd.blk       18.143   1.323  15.547  17.242
sd.res        8.938   0.303   8.541   8.715
sd.x         27.595   1.236  25.142  26.772
sigma         9.137   0.925   7.559   8.483
sigma.blk    25.505  13.189  12.020  17.461
deviance    434.157   4.532 427.636 430.749
                50%     75%   97.5%  Rhat n.eff
alpha       232.724 239.276 255.475 1.001  3000
beta          1.462   1.507   1.587 1.001  3000
beta.blk[1]  26.141  32.993  51.875 1.001  3000
beta.blk[2]   1.027   7.692  25.605 1.001  3000
beta.blk[3]   7.583  14.295  32.632 1.001  3000
beta.blk[4]  -1.678   4.896  22.754 1.002  3000
beta.blk[5] -29.028 -22.177  -3.990 1.001  3000
beta.blk[6]  -3.489   3.016  20.591 1.002  3000
res[1]       -4.930  -2.870   1.052 1.001  3000
res[2]       -1.346   0.681   4.299 1.001  3000
res[3]       10.713  12.706  16.390 1.001  3000
res[4]        8.199  10.371  14.888 1.001  3000
res[5]       -2.799  -0.674   3.426 1.001  2900
res[6]       -1.990   0.167   4.630 1.001  3000
res[7]        7.643   9.864  14.420 1.001  3000
res[8]        5.499   7.470  11.189 1.001  3000
res[9]       -7.045  -5.055  -1.437 1.001  3000
res[10]      -8.579  -6.277  -1.495 1.001  2900
res[11]      -1.575   0.708   5.352 1.001  2300
res[12]       2.393   4.735   9.359 1.001  2500
res[13]      -5.008  -3.056   1.027 1.002  1100
res[14]       4.048   6.175  10.178 1.002  1500
res[15]       0.294   2.346   6.608 1.002  1000
res[16]     -10.542  -8.577  -4.701 1.002  1300
res[17]      -0.389   1.586   5.720 1.002  1000
res[18]     -14.394 -12.025  -7.313 1.002  1100
res[19]       9.566  11.684  15.690 1.002  1600
res[20]      16.124  18.199  22.478 1.004   980
res[21]      -3.697  -1.195   3.666 1.001  3000
res[22]     -12.432 -10.396  -6.170 1.001  3000
res[23]       4.882   7.001  11.208 1.001  3000
res[24]      -3.627  -1.430   2.911 1.001  2900
res[25]      22.167  24.164  28.292 1.001  3000
res[26]      -1.904   0.046   4.021 1.001  3000
res[27]       4.352   6.673  11.173 1.001  2700
res[28]      -1.237   0.701   4.691 1.001  3000
res[29]      -7.639  -5.241  -0.691 1.001  3000
res[30]       0.241   2.178   6.136 1.001  3000
res[31]     -18.813 -16.841 -13.029 1.003  3000
res[32]      14.224  16.227  19.808 1.006  3000
res[33]       0.792   2.773   6.531 1.003  3000
res[34]      20.176  22.420  26.901 1.003  2900
res[35]       4.909   7.106  11.221 1.001  3000
res[36]      -7.349  -5.340  -1.645 1.002  3000
res[37]       6.185   8.333  12.381 1.001  3000
res[38]     -11.134  -8.688  -3.957 1.001  3000
res[39]     -12.649 -10.575  -6.714 1.002  3000
res[40]       1.953   3.979   7.877 1.002  3000
res[41]      -3.489  -1.459   2.898 1.001  3000
res[42]       0.523   2.444   6.654 1.001  3000
res[43]       1.599   3.565   7.879 1.001  3000
res[44]      -5.657  -3.696   0.374 1.001  3000
res[45]      -5.507  -3.561   0.405 1.001  3000
res[46]      -0.486   1.493   5.842 1.001  3000
res[47]      10.655  13.305  18.190 1.001  3000
res[48]     -15.163 -13.226  -9.216 1.001  3000
res[49]       6.670   8.624  12.799 1.001  3000
res[50]       3.945   5.908  10.114 1.001  3000
res[51]       4.616   6.583  10.265 1.006   340
res[52]      -8.021  -5.633  -1.069 1.006   380
res[53]      -2.420  -0.436   3.125 1.006   350
res[54]      -4.013  -1.952   1.880 1.005   450
res[55]     -12.558 -10.298  -6.036 1.004   640
res[56]       5.029   7.235  11.472 1.004   600
res[57]       5.108   7.143  10.842 1.005   400
res[58]       1.083   3.069   6.854 1.006   340
res[59]      10.361  12.394  16.464 1.006   420
res[60]      -0.659   1.364   4.970 1.006   360
sd.blk       18.151  19.019  20.733 1.001  2100
sd.res        8.876   9.095   9.697 1.002  3000
sd.x         27.600  28.443  29.948 1.001  3000
sigma         9.048   9.699  11.141 1.001  3000
sigma.blk    22.226  29.264  61.728 1.001  3000
deviance    433.308 436.654 444.924 1.001  3000

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = var(deviance)/2)
pD = 10.3 and DIC = 444.4
DIC is an estimate of expected predictive error (lower deviance is better).

Bayesian HMM

coefs <- data.rcb.jags$BUGSoutput$sims.matrix[,c('alpha','beta')]
xs <- seq(min(data.rcb$x), max(data.rcb$x), l=100)
Xmat <- model.matrix(~x, data.frame(x=xs))
head(Xmat)
  (Intercept)      x
1           1 0.9373
2           1 1.6292
3           1 2.3211
4           1 3.0130
5           1 3.7048
6           1 4.3967
pred <- coefs %*% t(Xmat)
library(plyr)
library(coda)
data.rcb.pred <- adply(pred,2,function(x) {
    data.frame(fit=median(x),HPDinterval(as.mcmc(x)))
    })
data.rcb.pred <- cbind(x=xs,data.rcb.pred)

ggplot(data.rcb.pred, aes(y=fit, x=x))+
#    geom_point(data=data.rcb, aes(y=res), col='grey')+
    geom_ribbon(aes(ymin=lower, ymax=upper),
                fill='blue', alpha=0.2)+
    geom_line()+
    theme_classic()+
    theme(axis.title.y=element_text(vjust=2),
          axis.title.x=element_text(vjust=-1))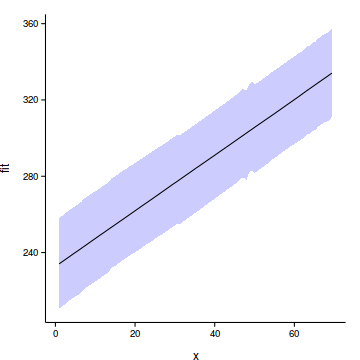
Xmat <- model.matrix(~x, data=data.rcb)
pred <- coefs %*% t(Xmat)
library(plyr)
library(coda)

res <- adply(
    data.rcb.jags$BUGSoutput$sims.matrix[,10:69],
    2,function(x) {
        data.frame(res=median(x))})$res

res <- adply(pred,2,function(x) {data.frame(fit=median(x))})$fit - res
data.rcb$res1 <- res

ggplot(data.rcb.pred, aes(y=fit, x=x))+
    geom_point(data=data.rcb, aes(y=res1), col='grey')+
    geom_ribbon(aes(ymin=lower, ymax=upper),
                fill='blue', alpha=0.2)+
    geom_line()+
    theme_classic()+
    theme(axis.title.y=element_text(vjust=2),
          axis.title.x=element_text(vjust=-1))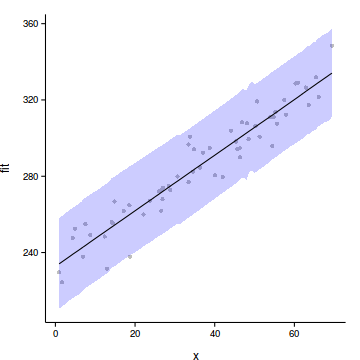

Nested design

data.nest <- read.csv('../data/data.nest.csv')
head(data.nest)
      y Region Sites Quads
1 32.26      A    S1     1
2 32.40      A    S1     2
3 37.20      A    S1     3
4 36.59      A    S1     4
5 35.45      A    S1     5
6 37.08      A    S1     6

Nested design

library(ggplot2)
data.nest$Sites <- factor(data.nest$Sites, levels=paste0('S',1:nSites))
ggplot(data.nest, aes(y=y, x=1,color=Region)) + geom_boxplot() +
    facet_grid(.~Sites) +
    scale_x_continuous('', breaks=NULL)+theme_classic()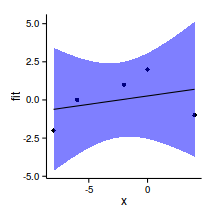

Nested design

#Effects of treatment
library(plyr)
boxplot(y~Region, ddply(data.nest, ~Region+Sites,
                        numcolwise(mean, na.rm=T)))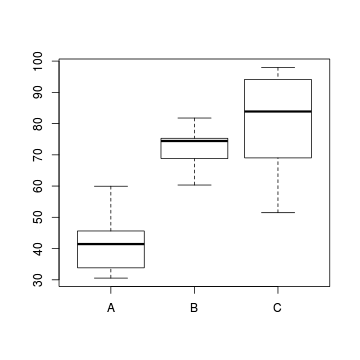

Nested design

#Site effects
boxplot(y~Sites, ddply(data.nest, ~Region+Sites+Quads,
                       numcolwise(mean, na.rm=T)))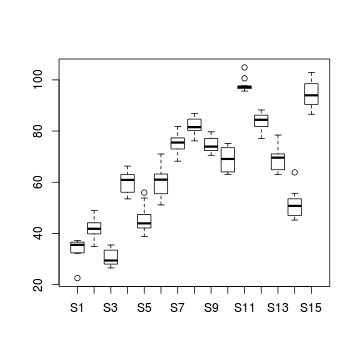

Nested design

library(nlme)
data.nest.lme <- lme(y~Region, random=~1|Sites, data.nest)
plot(data.nest.lme)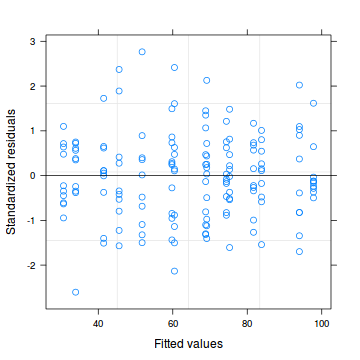

Nested design

plot(data.nest$Region, residuals(data.nest.lme,
      type='normalized'))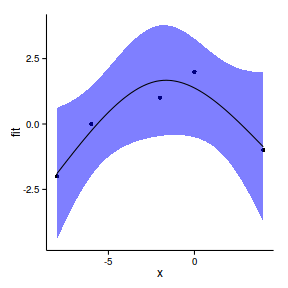

Nested design

summary(data.nest.lme)
Linear mixed-effects model fit by REML
 Data: data.nest 
    AIC   BIC logLik
  927.7 942.7 -458.9

Random effects:
 Formula: ~1 | Sites
        (Intercept) Residual
StdDev:       13.66    4.372

Fixed effects: y ~ Region 
            Value Std.Error  DF t-value p-value
(Intercept) 42.28     6.139 135   6.887  0.0000
RegionB     29.85     8.682  12   3.438  0.0049
RegionC     37.02     8.682  12   4.264  0.0011
 Correlation: 
        (Intr) ReginB
RegionB -0.707       
RegionC -0.707  0.500

Standardized Within-Group Residuals:
      Min        Q1       Med        Q3       Max 
-2.603787 -0.572952  0.004954  0.620915  2.765602 

Number of Observations: 150
Number of Groups: 15

Nested design

VarCorr(data.nest.lme)
Sites = pdLogChol(1) 
            Variance StdDev
(Intercept) 186.55   13.658
Residual     19.12    4.372
anova(data.nest.lme)
            numDF denDF F-value p-value
(Intercept)     1   135   331.8  <.0001
Region          2    12    10.2  0.0026

Nested design

library(multcomp)
summary(glht(data.nest.lme, linfct=mcp(Region="Tukey")))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lme.formula(fixed = y ~ Region, data = data.nest, random = ~1 | 
    Sites)

Linear Hypotheses:
           Estimate Std. Error z value Pr(>|z|)
B - A == 0    29.85       8.68    3.44   0.0017
C - A == 0    37.02       8.68    4.26   <0.001
C - B == 0     7.17       8.68    0.83   0.6867
              
B - A == 0 ** 
C - A == 0 ***
C - B == 0    
---
Signif. codes:  
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

Nested design

library(effects)
plot(allEffects(data.nest.lme))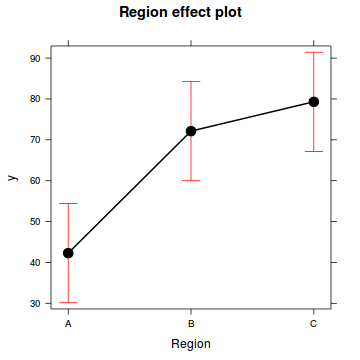

Linear mixed effects model

Summary figure

Step 1. gather model coefficients and model matrix

coefs <- fixef(data.nest.lme)
coefs
(Intercept)     RegionB     RegionC 
      42.28       29.85       37.02 
xs <- levels(data.nest$Region)
Xmat <- model.matrix(~Region, data.frame(Region=xs))
head(Xmat)
  (Intercept) RegionB RegionC
1           1       0       0
2           1       1       0
3           1       0       1

Linear mixed effects model

Summary figure

Step 3. calculate predicted y and CI

ys <- t(coefs %*% t(Xmat))
head(ys)
   [,1]
1 42.28
2 72.13
3 79.30
SE <- sqrt(diag(Xmat %*% vcov(data.nest.lme) %*% t(Xmat)))
CI <- 2*SE
#OR
CI <- qt(0.975,length(data.nest$y)-2)*SE
data.nest.pred <- data.frame(Region=xs, fit=ys, se=SE,
     lower=ys-CI, upper=ys+CI)
head(data.nest.pred)
  Region   fit    se lower upper
1      A 42.28 6.139 30.15 54.41
2      B 72.13 6.139 59.99 84.26
3      C 79.30 6.139 67.17 91.43

Linear mixed effects model

Summary figure

Step 4. plot it

with(data.nest.pred,plot.default(Region, fit,type='n',axes=F, ann=F,ylim=range(c(data.nest.pred$lower, data.nest.pred$upper))))
points(y~Region, data=data.nest, pch=16, col='grey')
points(fit~Region, data=data.nest.pred, pch=16)
with(data.nest.pred, arrows(as.numeric(Region),lower,as.numeric(Region),upper, length=0.1, angle=90, code=3))
axis(1, at=1:3, labels=levels(data.nest$Region))
mtext('Region',1,line=3)
axis(2,las=1)
mtext('Y',2,line=3)
box(bty='l')

Linear mixed effects model

Summary figure

Linear mixed effects model

Summary figure

Step 4. plot it

data.nest$res <- predict(data.nest.lme, level=0)-
    residuals(data.nest.lme)
with(data.nest.pred,plot.default(Region, fit,type='n',axes=F, ann=F,ylim=range(c(data.nest.pred$lower, data.nest.pred$upper))))
points(res~Region, data=data.nest, pch=16, col='grey')
points(fit~Region, data=data.nest.pred, pch=16)
with(data.nest.pred, arrows(as.numeric(Region),lower,as.numeric(Region),upper, length=0.1, angle=90, code=3))
axis(1, at=1:3, labels=levels(data.nest$Region))
mtext('Region',1,line=3)
axis(2,las=1)
mtext('Y',2,line=3)
box(bty='l')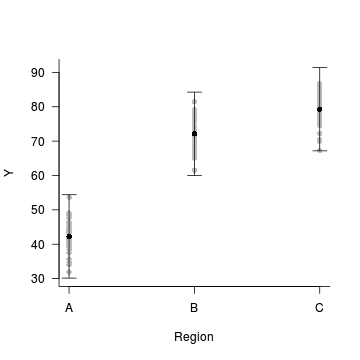

Linear mixed effects model

Summary figure

Linear mixed effects model

library(ggplot2)
data.nest$res <- predict(data.nest.lme, level=0)-
    residuals(data.nest.lme)

ggplot(data.nest.pred, aes(y=fit, x=Region))+
    geom_point(data=data.nest, aes(y=res), col='grey',position = position_jitter(height=0))+
    geom_errorbar(aes(ymin=lower, ymax=upper), width=0.1)+     
    geom_point()+
    theme_classic()+
    theme(axis.title.y=element_text(vjust=2),
          axis.title.x=element_text(vjust=-1))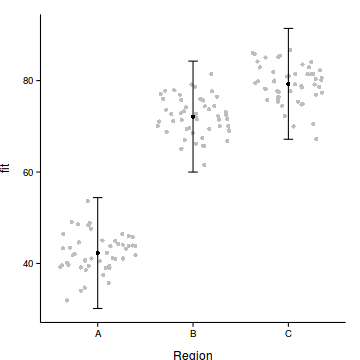

Linear mixed effects model

Bayesian HMM - nested

modelString = '
model{
   for (i in 1:n) {
     y[i] ~ dnorm(mu[i], tau)
     mu[i] <- alpha + beta.region[Region[i]] + beta.site[Sites[i]]
   }
   alpha ~ dnorm(0,1.0E-06)
   beta.region[1] <- 0
   for (i in 2:nRegion) {
     beta.region[i] ~ dnorm(0, 1.0E-06)
   }
   for (i in 1:nSite) {
     beta.site[i] ~ dnorm(0, tau.site)
   }
   tau <- 1/(sigma * sigma)
   tau.site <- 1/(sigma.site * sigma.site)
   sigma ~ dunif(0,100)
   sigma.site ~ dunif(0,100)
}
'
writeLines(modelString, con='HMM-nest.jags')
library(R2jags)

data.list <- with(data.nest, list(y=y, Region=as.numeric(Region),
          Sites=as.numeric(Sites),
          n=nrow(data.nest),
          nRegion=length(unique(Region)),
          nSite=length(unique(Sites))
                  ))
 
data.rcb.jags <- jags(data=data.list, inits=NULL,
                      param = c('alpha','beta.region','beta.site','sigma','sigma.site'),
                      model.file = 'HMM-nest.jags',
                      n.chains=3, n.iter=20000, n.burnin = 10000,
                      n.thin=10)
Compiling model graph
   Resolving undeclared variables
   Allocating nodes
   Graph Size: 497

Initializing model
print(data.rcb.jags)
Inference for Bugs model at "HMM-nest.jags", fit using jags,
 3 chains, each with 20000 iterations (first 10000 discarded), n.thin = 10
 n.sims = 3000 iterations saved
               mu.vect sd.vect    2.5%     25%
alpha           42.509   7.166  28.728  37.911
beta.region[1]   0.000   0.000   0.000   0.000
beta.region[2]  29.724  10.262   9.398  23.055
beta.region[3]  36.746  10.227  16.156  30.304
beta.site[1]    -8.663   7.278 -23.721 -13.053
beta.site[2]    -1.112   7.267 -16.027  -5.500
beta.site[3]   -11.892   7.288 -26.593 -16.333
beta.site[4]    17.270   7.249   2.359  12.816
beta.site[5]     3.069   7.304 -11.832  -1.477
beta.site[6]   -11.813   7.298 -26.322 -16.532
beta.site[7]     3.021   7.268 -12.009  -1.508
beta.site[8]     9.444   7.324  -5.287   4.734
beta.site[9]     2.188   7.332 -12.683  -2.443
beta.site[10]   -3.375   7.323 -18.090  -7.950
beta.site[11]   18.520   7.232   4.208  13.934
beta.site[12]    4.571   7.270  -9.885  -0.125
beta.site[13]  -10.111   7.282 -24.312 -14.558
beta.site[14]  -27.491   7.254 -41.878 -31.996
beta.site[15]   14.766   7.299   0.069  10.244
sigma            4.409   0.269   3.929   4.223
sigma.site      15.427   3.697  10.175  12.835
deviance       869.390   6.012 859.554 865.065
                   50%     75%   97.5%  Rhat
alpha           42.388  46.795  57.301 1.002
beta.region[1]   0.000   0.000   0.000 1.000
beta.region[2]  29.792  36.108  50.575 1.002
beta.region[3]  36.994  42.903  57.270 1.003
beta.site[1]    -8.467  -4.048   5.447 1.001
beta.site[2]    -1.010   3.450  13.257 1.002
beta.site[3]   -11.815  -7.213   2.385 1.002
beta.site[4]    17.440  21.858  31.416 1.002
beta.site[5]     3.236   7.799  17.353 1.002
beta.site[6]   -11.752  -7.202   2.434 1.001
beta.site[7]     3.039   7.531  17.378 1.001
beta.site[8]     9.451  14.006  23.916 1.001
beta.site[9]     2.156   6.770  16.808 1.001
beta.site[10]   -3.402   1.219  10.845 1.001
beta.site[11]   18.552  23.213  32.342 1.003
beta.site[12]    4.636   9.361  18.523 1.003
beta.site[13]  -10.001  -5.470   4.103 1.002
beta.site[14]  -27.389 -22.814 -13.516 1.002
beta.site[15]   14.887  19.382  29.256 1.002
sigma            4.396   4.576   4.963 1.001
sigma.site      14.841  17.316  24.462 1.001
deviance       868.667 872.931 883.239 1.001
               n.eff
alpha           2300
beta.region[1]     1
beta.region[2]  3000
beta.region[3]   850
beta.site[1]    2100
beta.site[2]    1700
beta.site[3]    2600
beta.site[4]    2600
beta.site[5]    2200
beta.site[6]    3000
beta.site[7]    3000
beta.site[8]    3000
beta.site[9]    3000
beta.site[10]   3000
beta.site[11]   1100
beta.site[12]   1400
beta.site[13]   1500
beta.site[14]   1600
beta.site[15]   1300
sigma           3000
sigma.site      3000
deviance        3000

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = var(deviance)/2)
pD = 18.1 and DIC = 887.5
DIC is an estimate of expected predictive error (lower deviance is better).

Bayesian HMM - nested

modelString = '
model{
   for (i in 1:n) {
     y[i] ~ dnorm(mu[i], tau)
     mu[i] <- alpha + beta.region[Region[i]] + beta.site[Sites[i]]
   }
   alpha ~ dnorm(0,1.0E-06)
   beta.region[1] <- 0
   for (i in 2:nRegion) {
     beta.region[i] ~ dnorm(0, 1.0E-06)
   }
   for (i in 1:nSite) {
     beta.site[i] ~ dnorm(0, tau.site)
   }
   tau <- 1/(sigma * sigma)
   tau.site <- 1/(sigma.site * sigma.site)
   sigma ~ dunif(0,100)
   sigma.site ~ dunif(0,100)

   #Posteriors
   Comp.A.B <- beta.region[1]-beta.region[2]
   Comp.A.C <- beta.region[1]-beta.region[3]
   Comp.B.C <- beta.region[2]-beta.region[3]
}
'
writeLines(modelString, con='HMM-nest.jags')
library(R2jags)

data.list <- with(data.nest, list(y=y, Region=as.numeric(Region),
          Sites=as.numeric(Sites),
          n=nrow(data.nest),
          nRegion=length(unique(Region)),
          nSite=length(unique(Sites))
                  ))
 
data.nest.jags <- jags(data=data.list, inits=NULL,
                      param = c('alpha','beta.region','beta.site','sigma','sigma.site','Comp.A.B','Comp.A.C','Comp.B.C'),
                      model.file = 'HMM-nest.jags',
                      n.chains=3, n.iter=20000, n.burnin = 10000,
                      n.thin=10)
Compiling model graph
   Resolving undeclared variables
   Allocating nodes
   Graph Size: 500

Initializing model
print(data.nest.jags)
Inference for Bugs model at "HMM-nest.jags", fit using jags,
 3 chains, each with 20000 iterations (first 10000 discarded), n.thin = 10
 n.sims = 3000 iterations saved
               mu.vect sd.vect    2.5%     25%
Comp.A.B       -29.689   9.893 -49.442 -35.969
Comp.A.C       -37.146   9.795 -56.963 -43.390
Comp.B.C        -7.457  10.180 -27.963 -13.870
alpha           42.425   6.914  28.952  38.170
beta.region[1]   0.000   0.000   0.000   0.000
beta.region[2]  29.689   9.893   9.627  23.622
beta.region[3]  37.146   9.795  18.483  30.899
beta.site[1]    -8.512   6.973 -22.722 -12.792
beta.site[2]    -0.974   7.029 -15.343  -5.127
beta.site[3]   -11.798   6.997 -26.417 -15.934
beta.site[4]    17.377   7.043   2.942  12.896
beta.site[5]     3.160   6.986 -11.218  -1.018
beta.site[6]   -11.688   7.176 -25.511 -16.278
beta.site[7]     3.139   7.154 -10.332  -1.526
beta.site[8]     9.556   7.155  -4.237   4.925
beta.site[9]     2.294   7.162 -11.576  -2.312
beta.site[10]   -3.251   7.183 -17.386  -7.709
beta.site[11]   18.259   7.228   4.151  13.734
beta.site[12]    4.318   7.290 -10.145  -0.195
beta.site[13]  -10.463   7.243 -24.724 -14.971
beta.site[14]  -27.843   7.250 -42.152 -32.342
beta.site[15]   14.462   7.274   0.320   9.890
sigma            4.410   0.267   3.940   4.225
sigma.site      15.347   3.677  10.105  12.807
deviance       869.309   5.943 859.845 865.006
                   50%     75%   97.5%  Rhat
Comp.A.B       -29.862 -23.622  -9.627 1.001
Comp.A.C       -37.119 -30.899 -18.483 1.002
Comp.B.C        -7.646  -1.097  12.319 1.003
alpha           42.473  46.683  56.651 1.001
beta.region[1]   0.000   0.000   0.000 1.000
beta.region[2]  29.862  35.969  49.442 1.001
beta.region[3]  37.119  43.390  56.963 1.002
beta.site[1]    -8.516  -4.234   4.860 1.001
beta.site[2]    -0.938   3.408  12.639 1.001
beta.site[3]   -11.850  -7.357   2.185 1.001
beta.site[4]    17.398  21.733  31.678 1.001
beta.site[5]     3.151   7.602  17.049 1.001
beta.site[6]   -11.622  -7.158   2.651 1.003
beta.site[7]     3.192   7.487  17.438 1.004
beta.site[8]     9.454  13.988  23.853 1.004
beta.site[9]     2.197   6.806  16.510 1.004
beta.site[10]   -3.308   1.209  10.771 1.003
beta.site[11]   18.159  22.705  32.842 1.001
beta.site[12]    4.292   8.872  19.044 1.001
beta.site[13]  -10.553  -5.939   3.717 1.001
beta.site[14]  -27.840 -23.341 -13.580 1.001
beta.site[15]   14.497  18.985  29.051 1.001
sigma            4.395   4.581   4.975 1.001
sigma.site      14.667  17.226  24.110 1.001
deviance       868.621 872.887 883.274 1.001
               n.eff
Comp.A.B        2600
Comp.A.C        3000
Comp.B.C         800
alpha           3000
beta.region[1]     1
beta.region[2]  2600
beta.region[3]  3000
beta.site[1]    3000
beta.site[2]    3000
beta.site[3]    3000
beta.site[4]    3000
beta.site[5]    3000
beta.site[6]     680
beta.site[7]     610
beta.site[8]     520
beta.site[9]     640
beta.site[10]    710
beta.site[11]   3000
beta.site[12]   3000
beta.site[13]   3000
beta.site[14]   3000
beta.site[15]   3000
sigma           3000
sigma.site      3000
deviance        3000

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = var(deviance)/2)
pD = 17.7 and DIC = 887.0
DIC is an estimate of expected predictive error (lower deviance is better).

Read world data examples

curdies <- read.csv('../data/curdies.csv', strip.white=T)
head(curdies)

SEASON SITE DUGESIA S4DUGES 1 WINTER 1 0.6477 0.8971 2 WINTER 1 6.0962 1.5713 3 WINTER 1 1.3106 1.0700 4 WINTER 1 1.7253 1.1461 5 WINTER 1 1.4594 1.0991 6 WINTER 1 1.0576 1.0141

library(ggplot2)
ggplot(curdies, aes(y=DUGESIA, x=SEASON))+geom_boxplot()+facet_wrap(~SITE)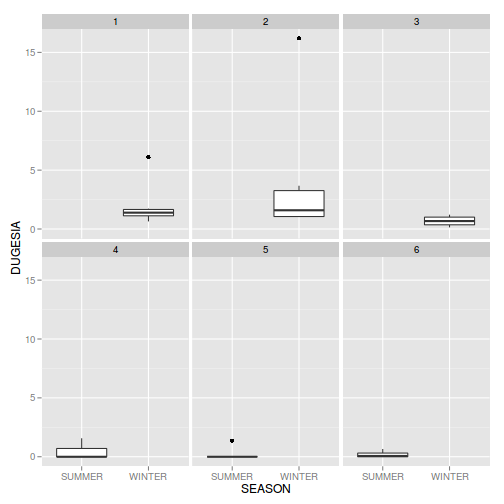
plot of chunk unnamed-chunk-43
plot of chunk unnamed-chunk-43
library(plyr)
curdies.ag <- ddply(curdies, ~SEASON+SITE, numcolwise(mean))

ggplot(curdies.ag, aes(y=DUGESIA, x=SEASON))+geom_boxplot()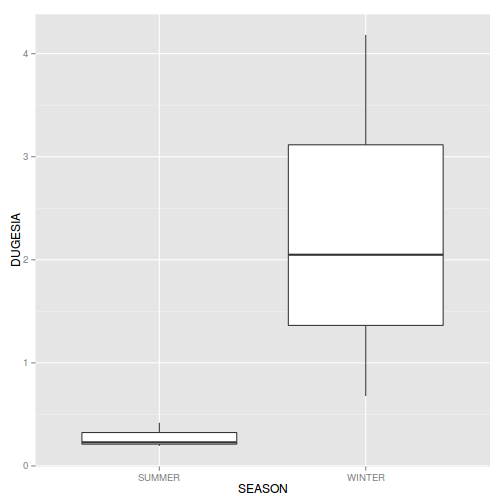
plot of chunk unnamed-chunk-43
plot of chunk unnamed-chunk-43
ggplot(curdies.ag, aes(y=S4DUGES, x=SEASON))+geom_boxplot()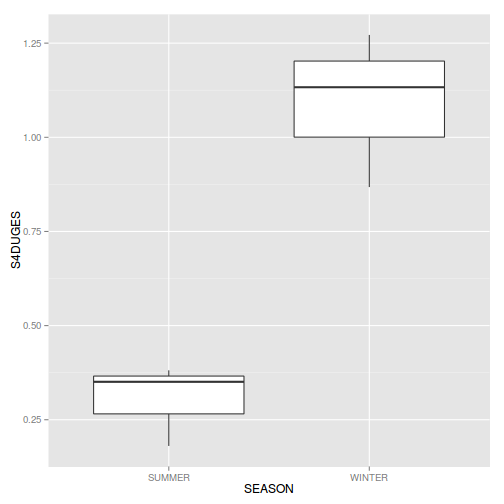
plot of chunk unnamed-chunk-43
plot of chunk unnamed-chunk-43
library(nlme)
curdies.lme <- lme(S4DUGES~SEASON, random=~1|SITE, data=curdies)
curdies.lme1 <- lme(S4DUGES~SEASON, random=~SEASON|SITE, data=curdies)
AIC(curdies.lme, curdies.lme1)
         df   AIC

curdies.lme 4 46.43 curdies.lme1 6 50.11

anova(curdies.lme, curdies.lme1)
         Model df   AIC   BIC logLik   Test

curdies.lme 1 4 46.43 52.54 -19.21
curdies.lme1 2 6 50.11 59.27 -19.05 1 vs 2 L.Ratio p-value curdies.lme
curdies.lme1 0.3208 0.8518

plot(curdies.lme)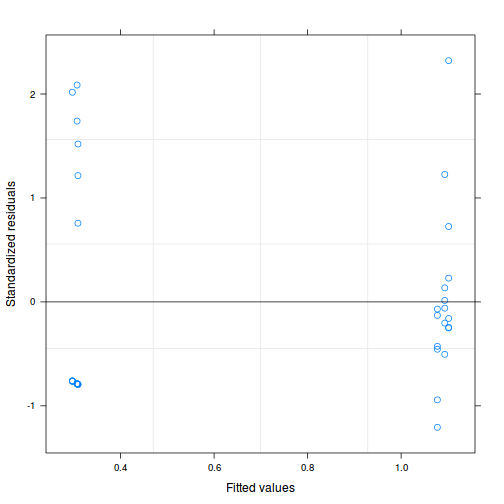
plot of chunk unnamed-chunk-43
plot of chunk unnamed-chunk-43
summary(curdies.lme)

Linear mixed-effects model fit by REML Data: curdies AIC BIC logLik 46.43 52.54 -19.21

Random effects: Formula: ~1 | SITE (Intercept) Residual StdDev: 0.04009 0.3897

Fixed effects: S4DUGES ~ SEASON Value Std.Error DF t-value p-value (Intercept) 0.3041 0.09472 30 3.211 0.0031 SEASONWINTER 0.7868 0.13395 4 5.873 0.0042 Correlation: (Intr) SEASONWINTER -0.707

Standardized Within-Group Residuals: Min Q1 Med Q3 Max -1.2065 -0.7681 -0.2481 0.3531 2.3209

Number of Observations: 36 Number of Groups: 6

#Calculate the confidence interval for the effect size of the main effect of season
intervals(curdies.lme)

Approximate 95% confidence intervals

Fixed effects: lower est. upper (Intercept) 0.1107 0.3041 0.4976 SEASONWINTER 0.4148 0.7868 1.1587 attr(,label) [1] Fixed effects:

Random Effects: Level: SITE lower est. upper sd((Intercept)) 1.875e-07 0.04009 8571

Within-group standard error: lower est. upper 0.3026 0.3897 0.5019

#unique(confint(curdies.lme,'SEASONWINTER')[[1]])
#Examine the ANOVA table with Type I (sequential) SS
anova(curdies.lme)
        numDF denDF F-value p-value

(Intercept) 1 30 108.5 <.0001 SEASON 1 4 34.5 0.0042

VarCorr(curdies.lme)

SITE = pdLogChol(1) Variance StdDev (Intercept) 0.001607 0.04009 Residual 0.151851 0.38968

vc<-as.numeric(as.matrix(VarCorr(curdies.lme))[,1])
vc/sum(vc)

[1] 0.01047 0.98953

curdies.lme2 <- lme(S4DUGES~1, random=~1|SEASON/SITE, data=curdies)
VarCorr(curdies.lme2)
        Variance     StdDev

SEASON = pdLogChol(1)
(Intercept) 0.300523 0.54820 SITE = pdLogChol(1)
(Intercept) 0.001607 0.04009 Residual 0.151851 0.38968

newdata <- data.frame(SEASON=levels(curdies$SEASON))
coefs <- fixef(curdies.lme)
Xmat <- model.matrix(~SEASON, data=newdata)
fit <- t(coefs %*% t(Xmat))

SE <- sqrt(diag(Xmat %*% vcov(curdies.lme) %*% t(Xmat)))
CI <- 2*SE
#OR
CI <- qt(0.975,length(curdies$SEASON)-2)*SE
newdata<- cbind(newdata, data.frame(fit=fit, se=SE,
     lower=fit-CI, upper=fit+CI))
head(newdata)

SEASON fit se lower upper 1 SUMMER 0.3041 0.09472 0.1116 0.4966 2 WINTER 1.0909 0.09472 0.8984 1.2834

ggplot(newdata, aes(y=fit, x=SEASON))+geom_point()+
    geom_errorbar(aes(ymin=lower, ymax=upper), width=0)+
    theme_classic()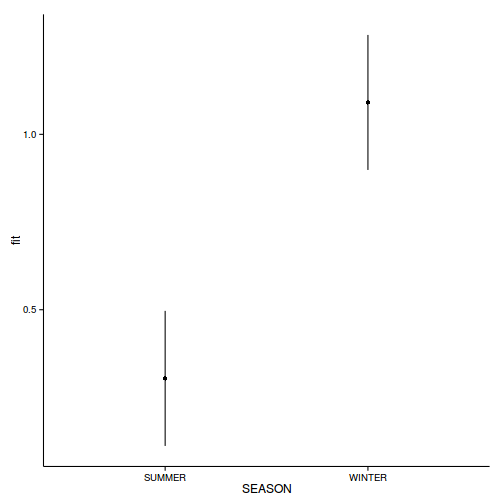
plot of chunk unnamed-chunk-43
plot of chunk unnamed-chunk-43

www.flutterbys.com.au/stats/downloads/data/

Format of copper.csv data file

COPPER PLATE DIST WORMS
.. .. .. ..



COPPER Categorical listing of the copper treatment (control = no copper applied, week 2 = copper treatment applied in second week and week 1= copper treatment applied in first week) applied to whole plates. Factor A (between plot factor).
PLATE Substrate provided for polychaete worm colonization on which copper treatment applied. These are the plots (Factor B). Numbers in this column represent numerical labels given to each plate.
DIST Categorical listing for the four concentric distances from the center of the plate (source of copper treatment) with 1 being the closest and 4 the furthest. Factor C (within plot factor)
WORMS Density (#/cm2) of worms measured. Response variable.

Saltmarsh 
copper <- read.csv('../data/copper.csv', strip.white=TRUE)

Read world data examples

Factor Effect Effects
Treat Fixed 2
Plate Random -
Dist Fixed 3 (or 1,2,3)
Treat x Dist Fixed 6 (or 2,..)
Plate x Treat x Dist Random -

Read world data examples

Questions:

  1. Does the copper treatment effect settlement?
  2. Does the copper treatment effect recruitment?
  3. Does distance to copper source effect recruitment?

Assumptions

  1. Linearity, Normality, homogeneity of variance
  2. Independence (or a specified dependency structure)

Exploratory data analysis

copper$PLATE <- factor(copper$PLATE)
copper$DIST <- as.factor(copper$DIST)
par(mfrow=c(1,2))
boxplot(WORMS ~ COPPER*DIST, data=copper)
boxplot(sqrt(WORMS)~ COPPER*DIST, data=copper)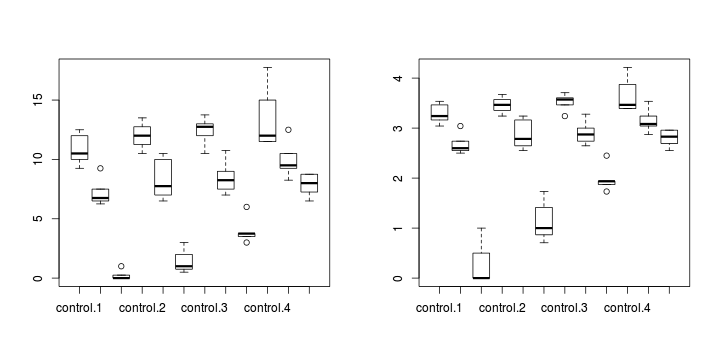

Exploratory data analysis

library(ggplot2)
ggplot(copper, aes(y=WORMS, x=DIST, color=COPPER)) +
    geom_boxplot()+theme_classic()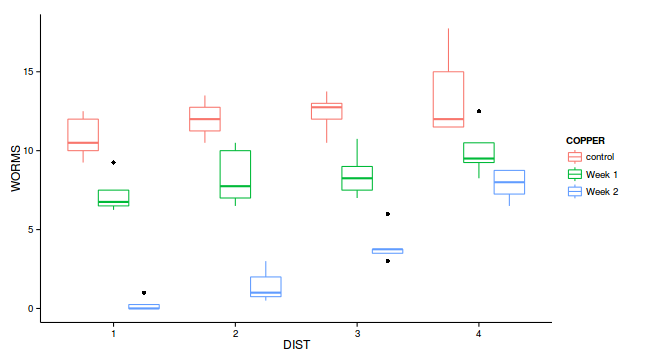

Exploratory data analysis

library(ggplot2)
library(gridExtra)
g1<-ggplot(copper, aes(y=WORMS, x=DIST, color=COPPER)) +
    geom_boxplot()+theme_classic()
g2<-ggplot(copper, aes(y=WORMS, x=DIST, color=COPPER)) +
    geom_boxplot()+
    scale_y_sqrt()+theme_classic()
grid.arrange(g1,g2, ncol=2)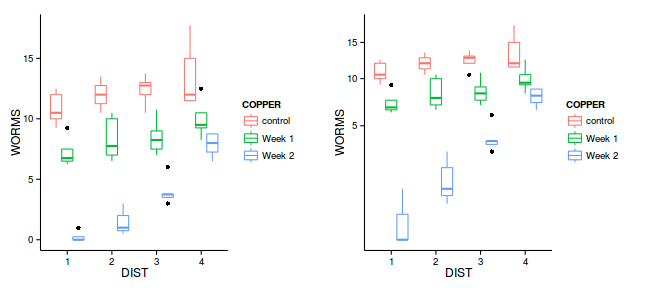

Exploratory data analysis

library(ggplot2)
library(gridExtra)
g1<-ggplot(copper, aes(y=WORMS, x=DIST, color=COPPER)) +
    geom_boxplot()+scale_color_discrete(guide=FALSE)+
    theme_classic()
g2<-ggplot(copper, aes(y=WORMS, x=DIST, color=COPPER)) +
    geom_boxplot()+scale_y_sqrt()+theme_classic()+
    theme(legend.position=c(1,0),
    legend.justification=c(1,0))
grid.arrange(g1,g2, ncol=2)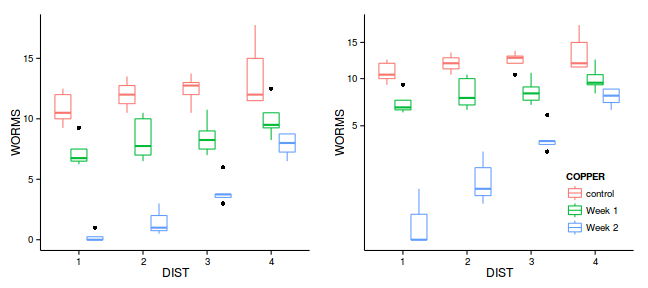

Exploratory data analysis

library(ggplot2)
ggplot(copper, aes(y=WORMS, x=as.numeric(DIST), color=COPPER)) +
    facet_wrap(~PLATE)+
    geom_line()+
    geom_point()+theme_classic()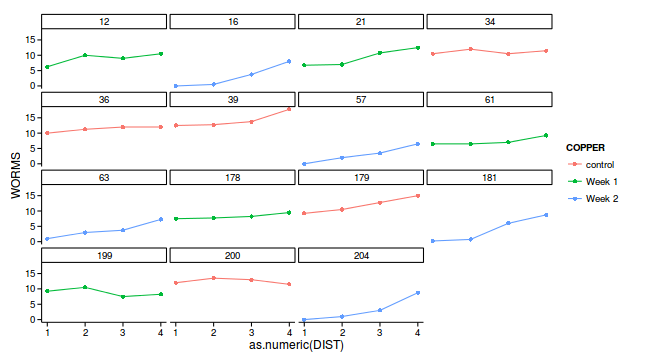

Exploratory data analysis

library(ggplot2)
ggplot(copper, aes(y=WORMS, x=as.numeric(DIST), group=PLATE)) +
    facet_wrap(~COPPER)+
    geom_line()+
    geom_point()+theme_classic()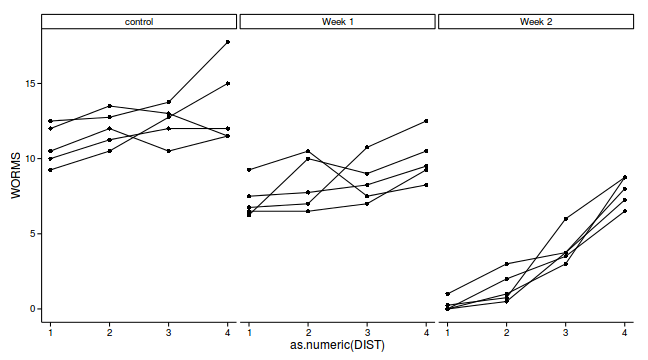

Fit mixed effects model

library(nlme)
copper.lme <- lme(WORMS ~ COPPER*DIST, random=~1|PLATE,
    data=copper, method='ML')
plot(residuals(copper.lme, type='normalized') ~ fitted(copper.lme))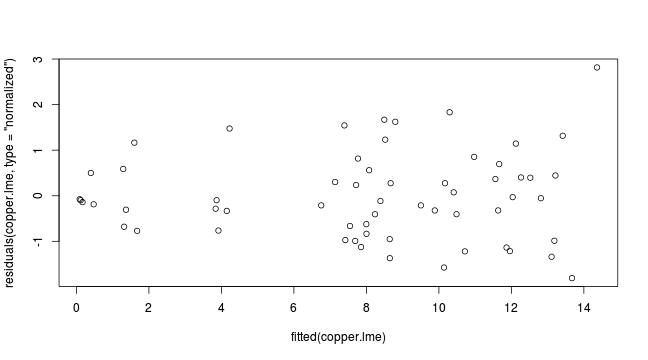
plot(residuals(copper.lme, type='normalized') ~ copper$DIST)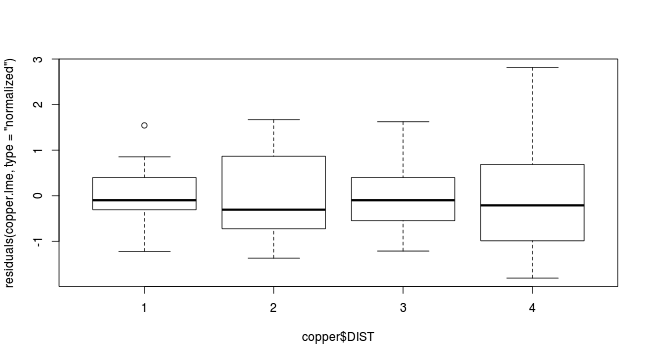
copper.lme1 <- update(copper.lme,
    correlation=corCompSymm(form=~1|PLATE))
anova(copper.lme, copper.lme1)
            Model df   AIC   BIC logLik   Test
copper.lme      1 14 228.3 257.6 -100.1       
copper.lme1     2 15 230.3 261.7 -100.1 1 vs 2
              L.Ratio p-value
copper.lme                   
copper.lme1 1.025e-10       1

Fit mixed effects model

library(nlme)
copper$iDIST <- as.numeric(copper$DIST)
copper.lme2 <- update(copper.lme,
    correlation=corAR1(form=~iDIST|PLATE))
#OR
copper.lme2 <- update(copper.lme,
    correlation=corAR1(form=~1|PLATE))
anova(copper.lme, copper.lme2)
            Model df   AIC   BIC  logLik   Test
copper.lme      1 14 228.3 257.6 -100.14       
copper.lme2     2 15 222.9 254.3  -96.47 1 vs 2
            L.Ratio p-value
copper.lme                 
copper.lme2   7.352  0.0067

Fit mixed effects model

copper.lme3 <- lme(WORMS ~ COPPER*iDIST, random=~1|PLATE,
   data=copper, method='ML',
   correlation=corAR1(form=~1|PLATE))
copper.lme4 <- lme(WORMS ~ COPPER*poly(iDIST,3),
   random=~1|PLATE, data=copper, method='ML',
   correlation=corAR1(form=~1|PLATE))
anova(copper.lme2, copper.lme3, copper.lme4)
            Model df   AIC   BIC  logLik   Test
copper.lme2     1 15 222.9 254.3  -96.47       
copper.lme3     2  9 220.5 239.3 -101.25 1 vs 2
copper.lme4     3 15 222.9 254.3  -96.47 2 vs 3
            L.Ratio p-value
copper.lme2                
copper.lme3   9.569   0.144
copper.lme4   9.569   0.144

Model validation

plot(copper.lme2)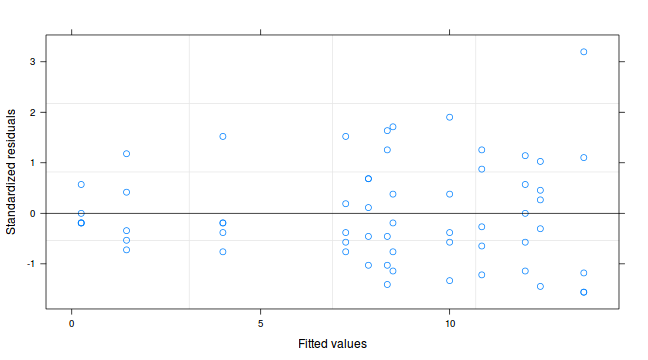
plot(residuals(copper.lme2, type='normalized')~copper$DIST)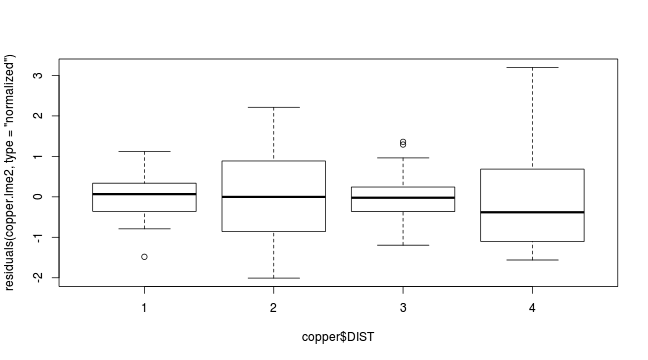
plot(residuals(copper.lme2, type='normalized')~copper$COPPER)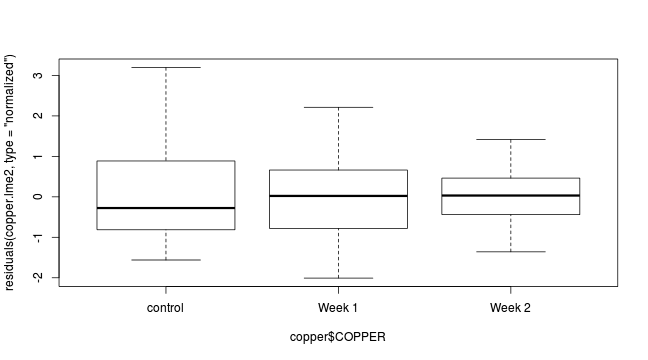

Fit mixed effects model

copper.lme <- lme(sqrt(WORMS) ~ COPPER*DIST, random=~1|PLATE,
    data=copper, correlation=corAR1(form=~1|PLATE),
    method='REML')
plot(copper.lme)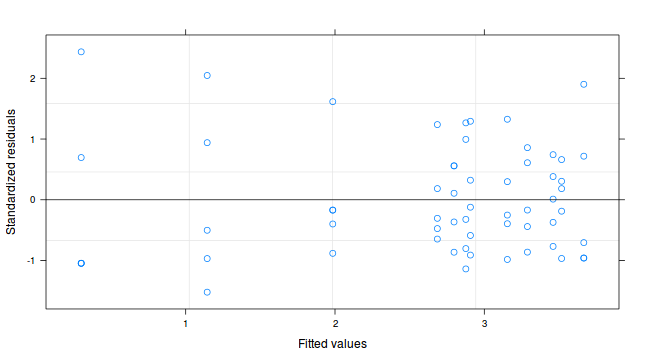
plot(residuals(copper.lme, type='normalized')~copper$DIST)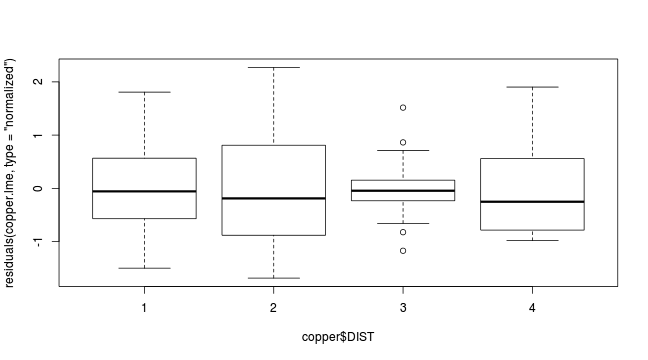
plot(residuals(copper.lme, type='normalized')~copper$COPPER)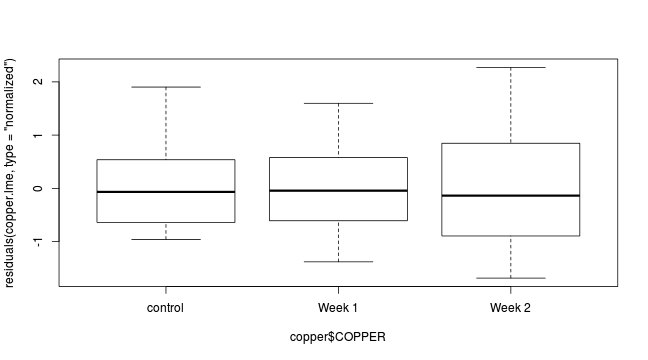

Summarize model

anova(copper.lme)
            numDF denDF F-value p-value
(Intercept)     1    36  3033.7  <.0001
COPPER          2    12   141.2  <.0001
DIST            3    36    39.7  <.0001
COPPER:DIST     6    36    15.8  <.0001
summary(copper.lme)
Linear mixed-effects model fit by REML
 Data: copper 
    AIC   BIC logLik
  60.49 88.56 -15.24

Random effects:
 Formula: ~1 | PLATE
        (Intercept) Residual
StdDev:   1.415e-05   0.2873

Correlation Structure: AR(1)
 Formula: ~1 | PLATE 
 Parameter estimate(s):
   Phi 
0.3701 
Fixed effects: sqrt(WORMS) ~ COPPER * DIST 
                    Value Std.Error DF t-value
(Intercept)         3.289    0.1285 36  25.598
COPPERWeek 1       -0.603    0.1817 12  -3.320
COPPERWeek 2       -2.989    0.1817 12 -16.449
DIST2               0.172    0.1442 36   1.193
DIST3               0.229    0.1688 36   1.357
DIST4               0.378    0.1770 36   2.134
COPPERWeek 1:DIST2  0.019    0.2039 36   0.093
COPPERWeek 2:DIST2  0.672    0.2039 36   3.295
COPPERWeek 1:DIST3 -0.007    0.2387 36  -0.031
COPPERWeek 2:DIST3  1.456    0.2387 36   6.100
COPPERWeek 1:DIST4  0.091    0.2504 36   0.364
COPPERWeek 2:DIST4  2.120    0.2504 36   8.466
                   p-value
(Intercept)         0.0000
COPPERWeek 1        0.0061
COPPERWeek 2        0.0000
DIST2               0.2408
DIST3               0.1833
DIST4               0.0397
COPPERWeek 1:DIST2  0.9268
COPPERWeek 2:DIST2  0.0022
COPPERWeek 1:DIST3  0.9752
COPPERWeek 2:DIST3  0.0000
COPPERWeek 1:DIST4  0.7182
COPPERWeek 2:DIST4  0.0000
 Correlation: 
                   (Intr) COPPERWk1 COPPERWk2
COPPERWeek 1       -0.707                    
COPPERWeek 2       -0.707  0.500             
DIST2              -0.561  0.397     0.397   
DIST3              -0.657  0.465     0.465   
DIST4              -0.689  0.487     0.487   
COPPERWeek 1:DIST2  0.397 -0.561    -0.281   
COPPERWeek 2:DIST2  0.397 -0.281    -0.561   
COPPERWeek 1:DIST3  0.465 -0.657    -0.328   
COPPERWeek 2:DIST3  0.465 -0.328    -0.657   
COPPERWeek 1:DIST4  0.487 -0.689    -0.344   
COPPERWeek 2:DIST4  0.487 -0.344    -0.689   
                   DIST2  DIST3  DIST4 
COPPERWeek 1                           
COPPERWeek 2                           
DIST2                                  
DIST3               0.585              
DIST4               0.463  0.653       
COPPERWeek 1:DIST2 -0.707 -0.414 -0.327
COPPERWeek 2:DIST2 -0.707 -0.414 -0.327
COPPERWeek 1:DIST3 -0.414 -0.707 -0.462
COPPERWeek 2:DIST3 -0.414 -0.707 -0.462
COPPERWeek 1:DIST4 -0.327 -0.462 -0.707
COPPERWeek 2:DIST4 -0.327 -0.462 -0.707
                   COPPERW1:DIST2 COPPERW2:DIST2
COPPERWeek 1                                    
COPPERWeek 2                                    
DIST2                                           
DIST3                                           
DIST4                                           
COPPERWeek 1:DIST2                              
COPPERWeek 2:DIST2  0.500                       
COPPERWeek 1:DIST3  0.585          0.293        
COPPERWeek 2:DIST3  0.293          0.585        
COPPERWeek 1:DIST4  0.463          0.232        
COPPERWeek 2:DIST4  0.232          0.463        
                   COPPERW1:DIST3 COPPERW2:DIST3
COPPERWeek 1                                    
COPPERWeek 2                                    
DIST2                                           
DIST3                                           
DIST4                                           
COPPERWeek 1:DIST2                              
COPPERWeek 2:DIST2                              
COPPERWeek 1:DIST3                              
COPPERWeek 2:DIST3  0.500                       
COPPERWeek 1:DIST4  0.653          0.327        
COPPERWeek 2:DIST4  0.327          0.653        
                   COPPERW1:DIST4
COPPERWeek 1                     
COPPERWeek 2                     
DIST2                            
DIST3                            
DIST4                            
COPPERWeek 1:DIST2               
COPPERWeek 2:DIST2               
COPPERWeek 1:DIST3               
COPPERWeek 2:DIST3               
COPPERWeek 1:DIST4               
COPPERWeek 2:DIST4  0.500        

Standardized Within-Group Residuals:
    Min      Q1     Med      Q3     Max 
-1.5204 -0.7759 -0.1780  0.6235  2.4366 

Number of Observations: 60
Number of Groups: 15 
VarCorr(copper.lme)
PLATE = pdLogChol(1) 
            Variance  StdDev   
(Intercept) 2.003e-10 1.415e-05
Residual    8.253e-02 2.873e-01

Summarize model

library(car)
interaction.plot(copper$DIST, copper$COPPER, copper$WORMS)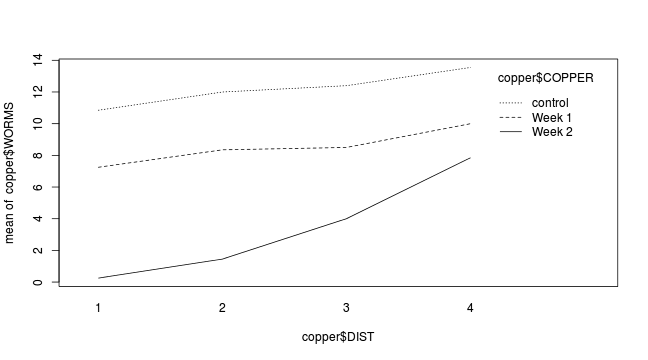
library(contrast)
contrast(copper.lme,
    a = list(COPPER = "control", DIST = levels(copper$DIST)),
    b = list(COPPER = "Week 1", DIST = levels(copper$DIST)))
lme model parameter contrast

 Contrast   S.E.  Lower  Upper    t df Pr(>|t|)
   0.6032 0.1817 0.2373 0.9692 3.32 45   0.0018
   0.5843 0.1817 0.2184 0.9503 3.22 45   0.0024
   0.6107 0.1817 0.2447 0.9766 3.36 45   0.0016
   0.5121 0.1817 0.1462 0.8781 2.82 45   0.0071
contrast(copper.lme,
    a = list(COPPER = "control", DIST = levels(copper$DIST)),
    b = list(COPPER = "Week 2", DIST = levels(copper$DIST)))
lme model parameter contrast

 Contrast   S.E.  Lower Upper     t df Pr(>|t|)
   2.9887 0.1817 2.6228 3.355 16.45 45        0
   2.3168 0.1817 1.9509 2.683 12.75 45        0
   1.5327 0.1817 1.1668 1.899  8.44 45        0
   0.8692 0.1817 0.5032 1.235  4.78 45        0
contrast(copper.lme,
    a = list(COPPER = "Week 1", DIST = levels(copper$DIST)),
    b = list(COPPER = "Week 2", DIST = levels(copper$DIST)))
lme model parameter contrast

 Contrast   S.E.     Lower Upper     t df
    2.386 0.1817  2.019569 2.751 13.13 45
    1.732 0.1817  1.366532 2.098  9.54 45
    0.922 0.1817  0.556056 1.288  5.07 45
    0.357 0.1817 -0.008912 0.723  1.97 45
 Pr(>|t|)
   0.0000
   0.0000
   0.0000
   0.0556
copper.lmeA <- lme(sqrt(WORMS) ~ COPPER*poly(iDIST,3), random=~1|PLATE,
    data=copper, correlation=corAR1(form=~1|PLATE),
    method='REML')
anova(copper.lmeA)
                      numDF denDF F-value p-value
(Intercept)               1    36  3033.7  <.0001
COPPER                    2    12   141.2  <.0001
poly(iDIST, 3)            3    36    39.7  <.0001
COPPER:poly(iDIST, 3)     6    36    15.8  <.0001
round(summary(copper.lmeA)$tTable,3)
                              Value Std.Error DF
(Intercept)                   3.483     0.084 36
COPPERWeek 1                 -0.578     0.119 12
COPPERWeek 2                 -1.927     0.119 12
poly(iDIST, 3)1               1.031     0.512 36
poly(iDIST, 3)2              -0.045     0.417 36
poly(iDIST, 3)3               0.179     0.360 36
COPPERWeek 1:poly(iDIST, 3)1  0.214     0.724 36
COPPERWeek 2:poly(iDIST, 3)1  6.186     0.724 36
COPPERWeek 1:poly(iDIST, 3)2  0.154     0.590 36
COPPERWeek 2:poly(iDIST, 3)2 -0.016     0.590 36
COPPERWeek 1:poly(iDIST, 3)3  0.147     0.508 36
COPPERWeek 2:poly(iDIST, 3)3 -0.202     0.508 36
                             t-value p-value
(Intercept)                   41.379   0.000
COPPERWeek 1                  -4.852   0.000
COPPERWeek 2                 -16.185   0.000
poly(iDIST, 3)1                2.015   0.051
poly(iDIST, 3)2               -0.108   0.915
poly(iDIST, 3)3                0.498   0.622
COPPERWeek 1:poly(iDIST, 3)1   0.295   0.769
COPPERWeek 2:poly(iDIST, 3)1   8.549   0.000
COPPERWeek 1:poly(iDIST, 3)2   0.261   0.795
COPPERWeek 2:poly(iDIST, 3)2  -0.028   0.978
COPPERWeek 1:poly(iDIST, 3)3   0.290   0.774
COPPERWeek 2:poly(iDIST, 3)3  -0.397   0.694
library(multcomp)
summary(glht(copper.lme, linfct=mcp(COPPER='Tukey')))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lme.formula(fixed = sqrt(WORMS) ~ COPPER * DIST, data = copper, 
    random = ~1 | PLATE, correlation = corAR1(form = ~1 | PLATE), 
    method = "REML")

Linear Hypotheses:
                      Estimate Std. Error z value
Week 1 - control == 0   -0.603      0.182   -3.32
Week 2 - control == 0   -2.989      0.182  -16.45
Week 2 - Week 1 == 0    -2.386      0.182  -13.13
                      Pr(>|z|)    
Week 1 - control == 0   0.0025 ** 
Week 2 - control == 0   <1e-04 ***
Week 2 - Week 1 == 0    <1e-04 ***
---
Signif. codes:  
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)
summary(glht(copper.lme, linfct=mcp(DIST='Tukey')))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lme.formula(fixed = sqrt(WORMS) ~ COPPER * DIST, data = copper, 
    random = ~1 | PLATE, correlation = corAR1(form = ~1 | PLATE), 
    method = "REML")

Linear Hypotheses:
           Estimate Std. Error z value Pr(>|z|)
2 - 1 == 0   0.1720     0.1442    1.19     0.63
3 - 1 == 0   0.2290     0.1688    1.36     0.52
4 - 1 == 0   0.3778     0.1770    2.13     0.14
3 - 2 == 0   0.0571     0.1442    0.40     0.98
4 - 2 == 0   0.2058     0.1688    1.22     0.61
4 - 3 == 0   0.1487     0.1442    1.03     0.73
(Adjusted p values reported -- single-step method)

Summary figure

newdata <- expand.grid(COPPER=levels(copper$COPPER), DIST=levels(copper$DIST))
Xmat <- model.matrix(~COPPER*DIST, data=newdata)
coefs <- fixef(copper.lme)
fit <- as.vector(Xmat %*% coefs)
newdata$fit <- fit^2
se<-sqrt(diag(Xmat %*% vcov(copper.lme) %*% t(Xmat)))
newdata$lower <- (fit-2*se)^2
newdata$upper <- (fit+2*se)^2
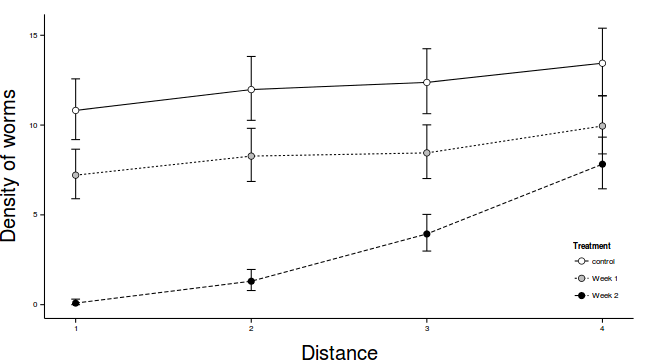
ggplot(newdata, aes(y=fit, x=as.numeric(DIST), color=COPPER))+
    geom_errorbar(aes(ymin=lower, ymax=upper), width=0.05)+
    geom_point()+geom_line()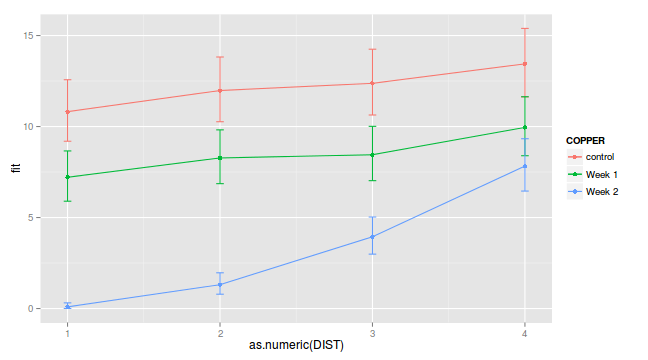

Summary figure

Bayesian

modelString="
model {
   #Likelihood
   for (i in 1:n) {
      y[i]~dnorm(mu[i],tau)
      mu[i] <- alpha0 + alpha[A[i]]+beta[Block[i]] + C.gamma[C[i]] + AC.gamma[A[i],C[i]] 
   }
   
   #Priors
   alpha0 ~ dnorm(0, 1.0E-6)
   alpha[1] <- 0
   for (i in 2:nA) {
     alpha[i] ~ dnorm(0, 1.0E-6) #prior
     AC.gamma[i,1] <- 0
   }
   for (i in 1:nBlock) {
     beta[i] ~ dnorm(0, tau.B) #prior
   }
   C.gamma[1] <- 0
   for (i in 2:nC) {
     C.gamma[i] ~ dnorm(0, 1.0E-6)
     AC.gamma[1,i] <- 0
   }
   AC.gamma[1,1] <- 0
   for (i in 2:nA) {
     for (j in 2:nC) {
       AC.gamma[i,j] ~ dnorm(0, 1.0E-6)
     }
   }
  
   sigma ~ dunif(0, 100)
   tau <- 1 / (sigma * sigma)
   sigma.B ~ dunif(0, 100)
   tau.B <- 1 / (sigma.B * sigma.B)
 }
"
writeLines(modelString,con="../BUGSscripts/splitPlot.jags")

data.list <- with(copper,
    list(y=sqrt(WORMS), 
         Block=as.numeric(PLATE),
         A=as.numeric(COPPER),
         C=as.numeric(DIST),
         n=nrow(copper), 
         nA = length(levels(COPPER)),
         nC = length(levels(DIST)),
         nBlock = length(levels(PLATE))
         )
) 

params <- c("alpha0","alpha",'C.gamma','AC.gamma',"sigma","sigma.B")
burnInSteps = 3000
nChains = 3 
numSavedSteps = 3000
thinSteps = 10
nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)
  
library(R2jags)
rnorm(1)

[1] -1.53

jags.f.time <- system.time( 
data.r2jags.f <- jags(data=data.list, 
      inits=NULL,
      parameters.to.save=params, 
      model.file="../BUGSscripts/splitPlot.jags",
      n.chains=nChains,
      n.iter=nIter, 
      n.burnin=burnInSteps,
      n.thin=thinSteps
      )
)

Compiling model graph Resolving undeclared variables Allocating nodes Graph Size: 349

Initializing model

print(data.r2jags.f)

Inference for Bugs model at ../BUGSscripts/splitPlot.jags, fit using jags, 3 chains, each with 13000 iterations (first 3000 discarded), n.thin = 10 n.sims = 3000 iterations saved mu.vect sd.vect 2.5% 25% AC.gamma[1,1] 0.000 0.000 0.000 0.000 AC.gamma[2,1] 0.000 0.000 0.000 0.000 AC.gamma[3,1] 0.000 0.000 0.000 0.000 AC.gamma[1,2] 0.000 0.000 0.000 0.000 AC.gamma[2,2] 0.014 0.256 -0.487 -0.157 AC.gamma[3,2] 0.670 0.250 0.177 0.502 AC.gamma[1,3] 0.000 0.000 0.000 0.000 AC.gamma[2,3] -0.009 0.247 -0.499 -0.169 AC.gamma[3,3] 1.457 0.255 0.960 1.282 AC.gamma[1,4] 0.000 0.000 0.000 0.000 AC.gamma[2,4] 0.091 0.249 -0.410 -0.071 AC.gamma[3,4] 2.119 0.252 1.620 1.955 C.gamma[1] 0.000 0.000 0.000 0.000 C.gamma[2] 0.172 0.180 -0.177 0.050 C.gamma[3] 0.229 0.178 -0.126 0.111 C.gamma[4] 0.378 0.174 0.028 0.260 alpha[1] 0.000 0.000 0.000 0.000 alpha[2] -0.600 0.197 -0.993 -0.727 alpha[3] -2.988 0.199 -3.392 -3.119 alpha0 3.289 0.140 3.014 3.198 sigma 0.278 0.032 0.224 0.255 sigma.B 0.111 0.065 0.010 0.064 deviance 14.470 8.355 -0.458 8.584 50% 75% 97.5% Rhat n.eff AC.gamma[1,1] 0.000 0.000 0.000 1.000 1 AC.gamma[2,1] 0.000 0.000 0.000 1.000 1 AC.gamma[3,1] 0.000 0.000 0.000 1.000 1 AC.gamma[1,2] 0.000 0.000 0.000 1.000 1 AC.gamma[2,2] 0.012 0.188 0.523 1.001 3000 AC.gamma[3,2] 0.665 0.838 1.156 1.001 3000 AC.gamma[1,3] 0.000 0.000 0.000 1.000 1 AC.gamma[2,3] -0.008 0.159 0.469 1.002 1100 AC.gamma[3,3] 1.453 1.624 1.971 1.002 1500 AC.gamma[1,4] 0.000 0.000 0.000 1.000 1 AC.gamma[2,4] 0.095 0.254 0.577 1.001 2400 AC.gamma[3,4] 2.117 2.284 2.619 1.001 3000 C.gamma[1] 0.000 0.000 0.000 1.000 1 C.gamma[2] 0.172 0.292 0.529 1.001 3000 C.gamma[3] 0.230 0.350 0.568 1.002 2000 C.gamma[4] 0.382 0.491 0.717 1.001 3000 alpha[1] 0.000 0.000 0.000 1.000 1 alpha[2] -0.603 -0.470 -0.223 1.001 3000 alpha[3] -2.986 -2.852 -2.610 1.001 2800 alpha0 3.288 3.382 3.562 1.001 3000 sigma 0.276 0.297 0.349 1.001 3000 sigma.B 0.106 0.150 0.252 1.029 180 deviance 14.233 19.709 32.181 1.003 970

For each parameter, n.eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = var(deviance)/2) pD = 34.9 and DIC = 49.3 DIC is an estimate of expected predictive error (lower deviance is better).

Bayesian