Inference (hypothesis) testing
lm –> LME
(integrate likelihood across all unobserved levels random effects)
lm –> LME
(integrate likelihood across all unobserved levels random effects)
glm —-………–> GLMM
Not so easy - need to approximate
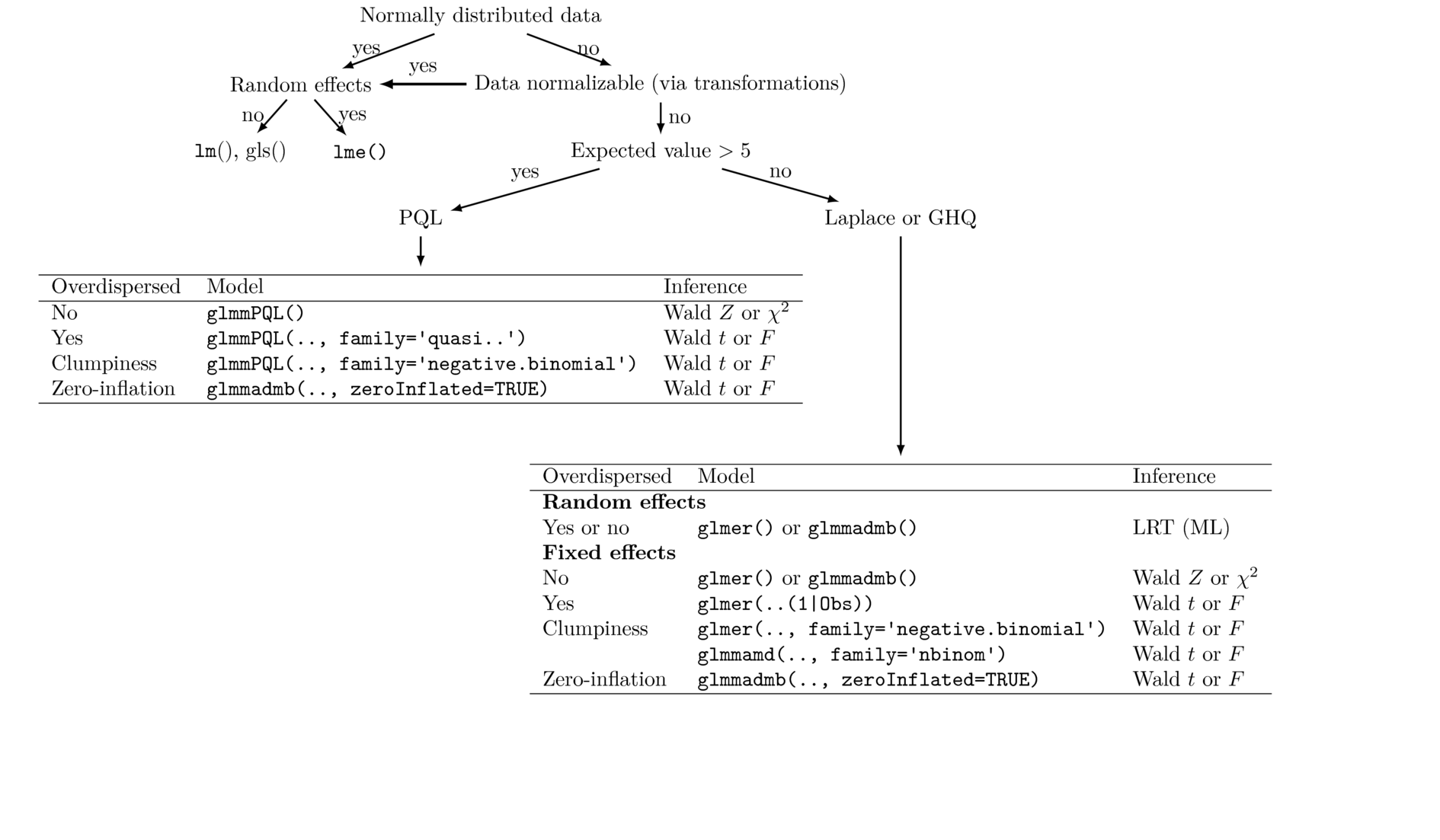
Penalized quasi-likelihood
Laplace approximation
Gauss-Hermite quadrature
Second-order Taylor series expansion - to approximate likelihood at unobserved levels of random effects
Second-order Taylor series expansion - to approximate likelihood at unobserved levels of random effects
Second-order Taylor series expansion - to approximate likelihood at unobserved levels of random effects
Depends on:
| Approximation | Characteristics | Associated inference | R function |
|---|---|---|---|
| Penalized Quasi-likelihood (PQL) | Fast and simple, accommodates heterogeneity and dependency structures, biased for small samples | Wald tests only | glmmPQL (MASS) |
| Laplace | More accurate (less biased), slower, does not accommodates heterogeneity and dependency structures | LRT | glmer (lme4), glmmadmb (glmmADMB) |
| Gauss-Hermite quadrature | Even more accurate (less biased), even slower, does not accommodates heterogeneity and dependency structures, cant handle more than 1 random effect | LRT | glmer (lme4)?? Does not seem to work |
| Markov Chain Monte Carlo (MCMC) | Bayesian, very flexible and accurate, yet very slow and complex | Bayesian credibility intervals, Bayesian P-values | Numerous (see this tutorial) |
| Feature | glmmPQL (MASS) | glmer (lme4) | glmmadmb (glmmADMB) | MCMC |
|---|---|---|---|---|
| Variance and covariance structures | Yes | - | not yet | Yes |
| Overdispersed (Quasi) families | Yes | - | - | Yes |
| Mixture families | limited | limited |
some|
Yes
|
|
| Complex nesting | Yes | Yes | Yes | Yes |
| Zero-inflation | - | - | Yes | Yes |
| Resid degrees of freedom | Between-Within | - | - | - |
| Parameter tests | Wald \(t\) | Wald \(z\) | Wald \(z\) | UI |
| Marginal tests (fixed effects) | Wald \(F\), \(\chi^2\) | Wald \(F\), \(\chi^2\) | Wald \(F\), \(\chi^2\) | UI |
| Marginal tests (Random effects) | Wald \(F\),\(\chi^2\) | LRT | LRT | UI |
| Information criterion | - | AIC | AIC | AIC, WAIC |

\[ \tiny \begin{align} log(y_{ij}) &= \gamma_{Site_i} + \beta_0 + \beta_1 Treat_{i} + \varepsilon_{ij} \hspace{1cm} \varepsilon \sim{} Pois(\lambda)\\ \text{where} \sum{\gamma}&=0 \end{align} \]