Workshop 10.4: Generalized linear models
Murray Logan
16 Aug 2016
Linear models
Other data types
- Binary - only 0 and 1 (dead/alive) (present/absent)
- Proportional abundance - range from 0 to 100
- Count data - min of zero
Linear models
- expected values outside logical bounds
- response not normally distributed
Logistic models
- expected values outside logical bounds
- response not normally distributed
Exponential family distributions
Gaussian distribution
Virtually unbound measurements (weight, lengths etc)
\(f(x\mid\mu, \sigma^2) = \frac{1}{\sqrt{2\sigma^2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
Binomial distribution
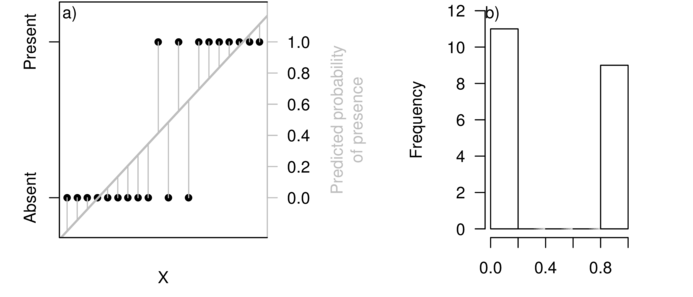
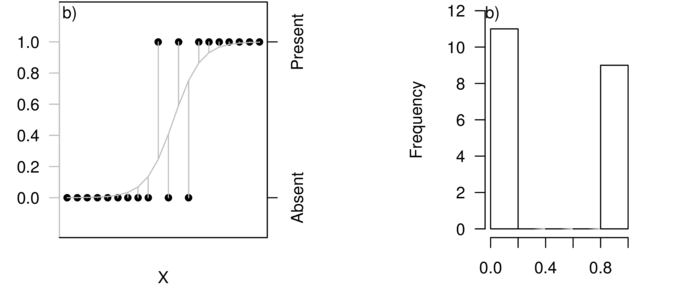
Presence/absence and data bound to the range [0,1]
\(f(k\mid n, p) = \binom{n}{p}p^k(1-p)^{n-k}\)
Poisson distribution
Count data (or count derivatives - like low densities)
\(f(x\mid \lambda) = \frac{e^{-\lambda}\lambda^x}{x!}\)
Negative Binomial
Count data (or count derivatives - like low densities)
\(f(x\mid \mu, \omega) = \frac{\Gamma(x + \omega)}{\Gamma(\omega)x!}\times\frac{\mu^x\omega^\omega}{(\mu + \omega)^{\mu+\omega}}\)
General linear models
\[\underbrace{E(Y)}_{Link~~function} = \underbrace{\beta_0 + \beta_1x_1~+~...~+~\beta_px_p}_{Systematic} + \varepsilon, ~~\varepsilon\sim Dist(...)\]
General linear models
\[\underbrace{E(Y)}_{Link~~function} = \underbrace{\beta_0 + \beta_1x_1~+~...~+~\beta_px_p}_{Systematic}~~\underbrace{~+~e}_{Random}\]
- Random component. \[E(Y_i) \sim{} N(\mu_i, \sigma^2)\] A nominated distribution (Gaussian, Poisson, Binomial, Gamma, Beta,…)
General linear models
\[\underbrace{E(Y)}_{Link~~function} = \underbrace{\beta_0 + \beta_1x_1~+~...~+~\beta_px_p}_{Systematic}~~\underbrace{~+~e}_{Random}\]
- Random component.
- Systematic component \[\beta_0 + \beta_1x_1~+~...~+~\beta_px_p\]
Generalized linear models
|
Response variable
|
Probability distribution
|
Link function
|
Model name
|
|
Continuous measurements
|
Gaussian
|
identity:
\(\mu\)
|
Linear regression
|
|
Binary
|
Binomial
|
logit:
\(log\left(\frac{\pi}{1-\pi}\right)\)
|
Logistic regression
|
|
|
|
probit:
\(\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\alpha+\beta.X} exp\left(-\frac{1}{2}Z^2\right)dZ\)
|
Probit regression
|
|
|
|
Complimentary log-log:
\(log(-log(1-\pi))\)
|
Logistic regression
|
|
Counts
|
Poisson
|
log:
\(log \mu\)
|
Poisson regression
log-linear model
|
|
|
Negative binomial
|
\(log\left(\frac{\mu}{\mu+\theta}\right)\)
|
Negative biomial regression
|
|
|
Quasi-poisson
|
\(log\mu\)
|
Poisson regression
|
OLS
Maximum Likelihood
\(f(x\mid\mu, \sigma^2) = \frac{1}{\sqrt{2\sigma^2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
\(ln\mathcal{L}(\mu, \sigma^2) = -\frac{n}{2}ln(2\pi)-\frac{n}{2}ln\sigma^2-\frac{1}{2\sigma^2}\sum^2_{i=1}(x_i-\mu)^2\)
Maximum likelihood estimates:
\(\hat{\mu} = \bar{x} = \frac{1}{n}\sum^n_{i=1}x_i\)
\(\hat{\sigma}^2 = \frac{1}{n}\sum^n_{i=1}(x_i-\bar{x})^2 \)
Maximum Likelihood
